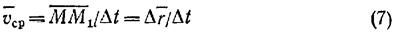чему равен вектор скорости точки в данный момент времени и какое направление он имеет
Вектор скорости точки



ВЕКТОР СКОРОСТИ ТОЧКИ
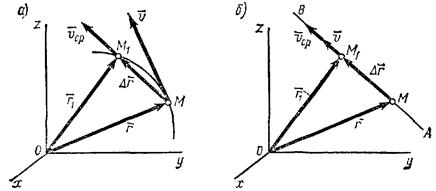
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором 
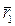
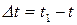
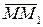
Из треугольника ОМ M1 видно, что 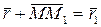
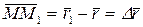
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени Δt:
Направлен вектор 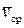
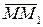
Очевидно, что чем меньше будет промежуток времени Δt, для которого вычислена средняя скорость, тем велича 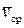
Скоростью точки в данный момент времени t называется векторная величина 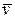
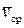
Предел отношения 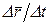
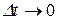
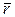
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.
Так как предельным направлением секущей ММ1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Формула (8) показывает также, что вектор скорости v̅ равен от-
отношению элементарного перемещения точки dr̅, направленного по
касательной к траектории, к соответствующему промежутку вре-
При прямолинейном движении вектор скорости v̅ все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно; при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости L/T, т. е. длина/время; качестве единиц измерения применяют обычно м/с или км/ч. Вопрос об определении модуля скорости будет рассмотрен в позже.
11. Чему равен вектор скорости точки в данный момент и какое направление он имеет?
А. Вектор скорости равен 
Б. Вектор скорости равен 
В. Вектор скорости равен 
Г. Вектор скоростей по модулю равен 
12. Какую размерность имеет скорость точки?
А. 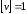




13. Как определяется алгебраическая величина скорости при естественном способе задания движения 
А. 



14. Точка движется по окружности согласно уравнению 
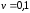
А. 



15. Как определяются проекции скорости точки на неподвижные оси координат?
А. 


Б. 


В. 


Г. 


16. Какой вид имеет годограф скорости при равномерном движении точки по какой–либо пространственной или плоской кривой?
А. Годографом скорости является кривая на сфере с радиусом, равным скорости точки.
Б. Годографом скорости является точка.
В. Годографом скорости является бесконечный отрезок прямой, параллельной траектории точки.
Г. Годографом скорости является дуга окружности с радиусом, равным скорости точки.
17. Движение точки задано уравнениями 


А. 

В. 

18. Что характеризует ускорение точки?
А. Ускорение точки характеризует быстроту и направление движения.
Б. Ускорение точки характеризует быстроту изменения модуля и направления скорости точки.
В. Ускорение характеризует перемещение точки по траектории.
Г. Ускорение точки как векторная величина характеризует быстроту изменения величины и направления скорости точки.
19. Чему равен вектор ускорения точки и как он направлен по отношению к годографу скорости?
А. Вектор ускорения точки 
Б. Вектор ускорения точки равен 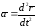
В. Вектор ускорения точки равен 
Г. Вектор ускорения точки равен 
20. Какие оси называются естественными осями?
А. Любые три оси называются естественными осями.
Б. Две взаимно-перпендикулярные оси называются естественными осями.
В. Естественными координатными осями называются три взаимно перпендикулярные оси (начало которых совпадают с движущейся точкой): 1) касательная, направленная в сторону возрастания дуговой координаты; 2) главная нормаль, направленная в сторону вогнутости кривой;
Г. Система координат с началом в точке кривой, осями которой служит касательная, главная нормаль и бинормаль, называют естественным трехгранником.
21. Как определяется кривизна траектории в данной точке?
А. 

Б. 


В. 
Г. 
22. В какой плоскости расположено ускорение точки?
А. В нормальной плоскости.
Б. В плоскости перпендикулярной к нормальной и соприкасающейся плоскостям (в спрямляющей плоскости).
В. В соприкасающейся плоскости.
Г. В плоскости, проходящей через две касательные, проведенные в двух бесконечно близких точках траектории.
23. Как определяется и что характеризует касательное ускорение точки?
А. Касательное ускорение 
Б. Касательное ускорение 
В. Касательное ускорение 
Г. Касательное ускорение 
24. Как определяется и что характеризует нормальное ускорение точки?
А. Нормальное ускорение равно 
Б. Нормальное ускорение равно 
В. Нормальное ускорение равно 
Г.Нормальное ускорение равно 
25. Классифицируйте движение точки по ускорениям.
А. Если 

Б. Если 

В. Если 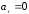

Г. Если 

26. Проекции скорости точки во время движения определяются выражениями 
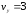

А. 

Б. 

В. 

Г. 

27. Точка М по закону 




28. По окружности радиуса 


А. 







29. Определить скорость точки, когда радиус кривизны траектории 



А. 



Глава II. Простейшие движения твердого тела
§4. ПОступательное движение твердого тела
30. О чем гласит основная теорема кинематики твердого тела?
А. Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, не равны.
Б. Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой 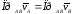
В. Проекции скоростей двух точек тела на ось, проходящую через эти точки, равны при любом движении тела.
Г. Скорость любой точки твердого тела равна векторной сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
Используя основную теорему кинематики твердого тела, определите скорость ползуна 

А. 
Б. 

В. 

Г. 

32. Какое движение твердого тела называется поступательным?
А. Поступательным движением твердого тела называют такое движение тела, при котором все точки тела движутся в плоскостях параллельных некоторой неподвижной плоскости.
Б. Поступательным называется такое движение твердого тела, при котором любая прямая, взятая в теле, во все время движения остается параллельной своему начальному положению.
В. Поступательным называется движение тела, при котором любая прямая в этом теле перемещается, оставаясь параллельной своему первоначальному направлению.
Г. Поступательным называется движение тела, при котором любая прямая в этом теле перемещается, оставаясь перпендикулярной к некоторой неподвижной плоскости.