Информационная энтропия в чем измеряется

Информационная энтропия: определение понятия, свойства, система

Понятие информационной энтропии подразумевает отрицательный логарифм функции массы вероятности для значения. Таким образом, когда источник данных имеет значение с меньшей вероятностью (т. е., когда происходит событие с низкой вероятностью), событие переносит больше «информации» («сюрприз»), чем, когда исходные данные имеют значение с более высокой вероятностью.

Объем информации, передаваемый каждым событием, определенным таким образом, становится случайной величиной, ожидаемым значением которой является информационная энтропия. Как правило, энтропия относится к беспорядку или неопределенности, а ее определение, используемое в теории информации, непосредственно аналогично определению, используемому в статистической термодинамике. Концепция ИЭ была введена Клодом Шенноном в его статье 1948 года «Математическая теория коммуникации». Отсюда и возник термин «информационная энтропия Шеннона».

Вам будет интересно: Понятие истины и ее критерии: определение, особенности, общая характеристика

Определение и система

Базовая модель системы передачи данных состоит из трех элементов: источника данных, канала связи и приемника, и, как выражается Шеннон, «основная проблема связи» заключается в том, чтобы получатель мог идентифицировать, какие данные были сгенерированы источником, на основе сигнала, который он получает по каналу. Энтропия обеспечивает абсолютное ограничение на кратчайшую возможную среднюю длину кодирования без потерь сжатых данных по источнику. Если энтропия источника меньше пропускной способности канала связи, данные, генерируемые им, могут быть надежно переданы приемнику (по крайней мере теоретически, возможно, пренебрегая некоторыми практическими соображениями, такими как сложность системы, необходимой для передачи данных и количества времени, которое может потребоваться для передачи данных).

Вам будет интересно: Основные языковые уровни: понятие, классификация и виды

Информационная энтропия обычно измеряется в битах (альтернативно называемых «шэннонами») или иногда в «естественных единицах» (nats) или десятичных разрядах (называемых «dits», «bans» или «hartleys»). Единица измерения зависит от базы логарифма, которая используется для определения энтропии.

Свойства и логарифм

Поскольку наблюдение менее вероятных событий происходит реже, нет ничего общего, что энтропия (считающаяся средней информацией), полученная из неравномерно распределенных данных, всегда меньше или равна log2 (n). Энтропия равна нулю, когда один результат определен.

Информационная энтропия Шеннона количественно определяет эти соображения, когда известно распределение вероятностей исходных данных. Смысл наблюдаемых событий (смысл сообщений) не имеет значения в определении энтропии. Последняя учитывает только вероятность наблюдения определенного события, поэтому информация, которую оно инкапсулирует, представляет собой данные о лежащих в основе распределения возможностях, а не о значении самих событий. Свойства информационной энтропии при этом остаются теми же, что описывались выше.

Теория информации

Основная идея теории информации заключается в том, что чем больше человек знает о теме, тем меньше информации о ней можно получить. Если событие очень вероятно, это не удивительно, когда это происходит и, следовательно, дает мало новой информации. И наоборот, если событие было невероятным, гораздо более информативным было то, что произошло событие. Следовательно, информационное наполнение является возрастающей функцией обратного вероятности события (1 / p).

Теперь, если произойдет больше событий, энтропия измеряет средний информационный контент, который вы можете ожидать, если произойдет одно из событий. Это означает, что литье штампа имеет больше энтропии, чем бросание монеты, потому что каждый результат кристалла имеет меньшую вероятность, чем каждый результат монеты.

Особенности

Таким образом, энтропия является мерой непредсказуемости состояния или, что тоже самое, его среднего информационного содержания. Чтобы получить интуитивное понимание этих терминов, рассмотрите пример политического опроса. Обычно такие опросы случаются, потому что результаты, например, выборов еще не известны.

Другими словами, результаты опроса относительно непредсказуемы, и на самом деле его проведение и изучение данных дают некоторую новую информацию; это просто разные способы сказать, что априорная энтропия результатов опроса велика.

Теперь рассмотрим случай, когда один и тот же опрос выполняется второй раз вскоре после первого. Поскольку результат первого опроса уже известен, показатели второго опроса могут быть хорошо предсказаны, и результаты не должны содержать много новой информации; в этом случае априорная энтропия второго результата опроса мала по сравнению с первой.

Бросок монеты

Теперь рассмотрим пример броска монеты. Предполагая, что вероятность решки совпадает с вероятностью орла, энтропия броска монеты имеет очень высокое значение, поскольку является своеобразным примером информационной энтропии системы.

Напротив, бросок монеты, использующей обе стороны с решками и без орлов, имеет нулевую энтропию, так как монета всегда упадет на этот знак, и результат можно предсказать отлично.

Заключение

Если схема сжатия не имеет потерь, то есть вы всегда можете восстановить все исходное сообщение, распаковывая, тогда сжатое сообщение имеет такое же количество информации, что и оригинал, но передается меньшим количеством символов. То есть он имеет больше информации или более высокую энтропию на каждый символ. Это означает, что сжатое сообщение имеет меньшую избыточность.

Грубо говоря, теорема о кодировании исходного кода Шеннона гласит: схема сжатия без потерь не может сокращать сообщения в среднем, чтобы иметь более одного бита информации на бит сообщения, но может быть достигнуто любое значение, меньшее одного бита информации на бит сообщения, используя подходящую схему кодирования. Энтропия сообщения в битах, умноженная на его длину, является мерой того, сколько общей информации содержится в нем.

Источник

Введение в понятие энтропии и ее многоликость

Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.

В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.

Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона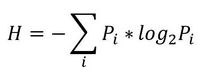
, где Pi это вероятность наступления i-го исхода.

То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событие более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.

Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.

Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).

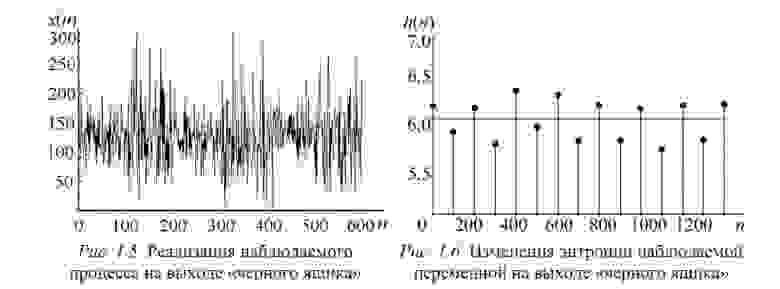
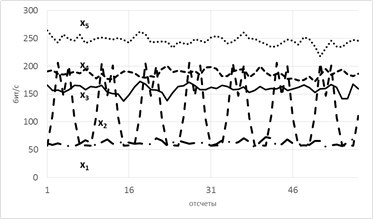
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.

Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).

Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).

Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.

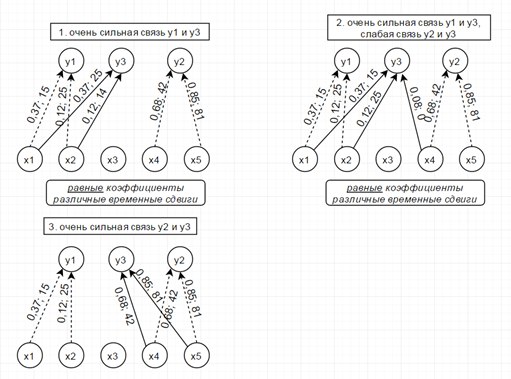
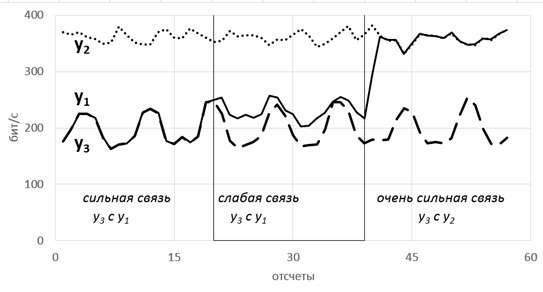
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).

Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!

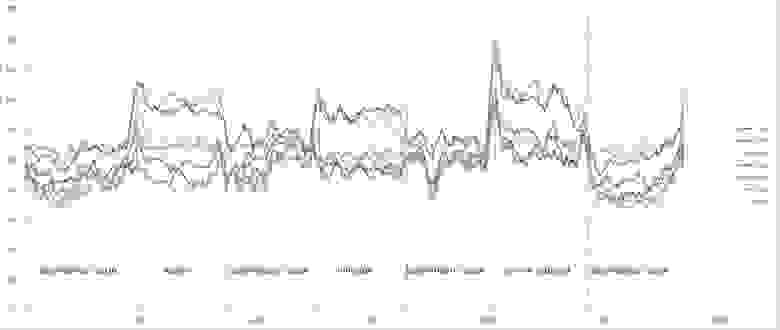
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.

Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).

Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.

Источник

Энтропия (в теории информации)

В теории информации, энтропия Шеннона, или информационная энтропия — мера неопределённости, связанной со случайной величиной (с.в.); определяет количество информации, содержавшейся в сообщении (обычно в битах или битах на символ); минимальная длина сообщения, необходимая для передачи информации; также абсолютный предел наиболее возможного сжатия без потерь любого сообщения: при представлении сообщения рядом символов, кратчайшее представление, необходимое для передачи сообщения — это энтропия Шеннона в битах на символ, умноженная на число символов в исходном сообщении.

Эквивалентно, энтропия Шеннона — мера среднего информационного содержания с.в., которое наблюдатель (получатель сообщения) теряет, когда ему неизвестно значение (исход) с.в.

Содержание

Определение

Энтропия Шеннона дискретной с.в. , которая может принимать значения , равна величине

Характеризация

Определим и меру информационной энтропии

Информационная энтропия характеризуется следующими пожеланиями (desiderata):

Непрерывность Мера должна быть непрерывной — то есть, изменение значения одной из вероятностей на очень маленькую величину должно изменить энтропию также на маленькую величину. Симметрия Мера не должна меняться, если исходы переупорядочены: и т.д. Максимум Мера должна быть максимальной, если все исходы одинаково вероятны (неопределённость является самой высокой, когда все возможные события равновероятны). Для равновероятных событий энтропия должна увеличиваться с увеличением их числа: Аддитивность Количество энтропии не должно зависеть от того, как система событий разделена на части (подсистемы). Это последнее функциональное отношение характеризует энтропию системы с подсистемами и требует, чтобы энтропия системы могла быть вычислена через энтропии ее подсистем, если мы знаем, как подсистемы взаимодействуют с друг другом. Дан ансамбль из равномерно распределённых элементов, которые произвольно разделены на коробок (подсистем) с элементами соответственно; энтропия всего ансамбля должна быть равна сумме энтропии системы коробок и индивидуальных энтропий коробок, взвешенных с вероятностью обнаружения элемента в соответстувующей коробке. Для положительных целых чисел , Выбор подразумевает, что энтропия конкретного исхода равна нулю:

Можно показать, что любое определение энтропии, удовлетворяющее этим предположениям имеет форму

где — постоянная, соответствующая выбору единицы измерения.

Пояснения

Пример

Дальнейшие свойства

Увеличение энтропии Байеса — закон, согласно которому по мере увеличения выборки сравнения объектов А` для идентификации объекта А, индивидуальные особенности объекта А размываются по отношению к выборке, а идентификация становится бессмысленной. Другими словами с увеличение выборки у объекта А по отношению к ней увеличивается энтропия.

Считается, что закон был открыт эмпирически, до его математического доказательства британским математиком Томасом Байесом. В настоящее время в разных интерпретациях используется в кибернетике, информатике, теории систем, менеджменте и других науках. Некоторые математики и физики считают этот закон еще одним из начал термодинамики.

Пример. Если кто-то захочет установить личность человека, попавшего на видеокамеры, то процесс будет становится тем более бессмысленным, чем с большим количеством людей будет сравнен человек.

Источник

Информационная энтропия в чем измеряется

Установив, что случайные процессы являются адекватной моделью сигналов, мы получаем возможность воспользоваться результатами и мощным аппаратом теории случайных процессов. Это не означает, что теория вероятностей и теория случайных процессов дают готовые ответы на все вопросы о сигналах: подход с новых позиций выдвигает такие вопросы, которые просто не возникали. Так и родилась теория информации, специально рассматривающая сигнальную специфику случайных процессов. При этом были построены принципиально новые понятия и получены новые, неожиданные результаты, имеющие характер научных открытий.

Понятие неопределенности

Первым специфическим понятием теории информации является понятие неопределенности случайного объекта, для которого удалось ввести количественную меру, названную энтропией. Начнем с простейшего примера — со случайного события. Пусть, например, некоторое событие может произойти с вероятностью 0,99 и не произойти с вероятностью 0,01, а другое событие имеет вероятности соответственно 0,5 и 0,5. Очевидно, что в первом случае результатом опыта «почти наверняка» является наступление события, во втором же случае неопределенность исхода так велика, что от прогноза разумнее воздержаться.

Для характеристики размытости распределения широко используется второй центральный момент (дисперсия) или доверительный интервал. Однако эти величины имеют смысл лишь для случайных числовых величин и не могут применяться к случайным объектам, состояния которых различаются качественно. Следовательно, мера неопределенности, связанной с распределением, должна быть некоторой его числовой характеристикой, функционалом от распределения, никак не связанным с тем, в какой шкале измеряются реализации случайного объекта.

Энтропия и ее свойства

Примем (пока без обоснования) в качестве меры неопределенности случайного объекта А с конечным множеством возможных состояний А1. Аn с соответствующими вероятностями P₁,P₂. P_n величину

которую и называют энтропией случайного объекта А (или распределения < >. Убедимся, что этот функционал обладает свойствами, которые вполне естественны для меры неопределенности.

Как видим, свойства функционала Н позволяют использовать его в качестве меры неопределенности.

Дифференциальная энтропия

Обобщение столь полезной меры неопределенности на непрерывные случайные величины наталкивается на ряд сложностей, которые, однако, преодолимы. Прямая аналогия

не приводит к нужному результату: плотность p(x) является размерной величиной (размерность плотности p(x) обратно пропорциональна x а логарифм размерной величины не имеет смысла. Однако положение можно исправить, умножив p(x) под знаком логарифма на величину К, имеющую туже размерность, что и величина х:

Теперь величину К можно принять равной единице измерения х, что приводит к функционалу

который получил название «дифференциальной энтропии». Это аналог энтропии дискретной величины, но аналог условный, относительный: ведь единица измерения произвольна. Запись (3) означает, что мы как бы сравниваем неопределенность случайной величины, имеющей плотность p(x), с неопределенностью случайной величины, равномерно распределенной в единичном интервале. Поэтому величина h(X) в отличие от Н(Х) может быть не только положительной. Кроме того, h(X) изменяется при нелинейных преобразованиях шкалы х, что в дискретном случае не играет роли. Остальные свойства h(X) аналогичны свойствам Н(Х), что делает дифференциальную энтропию очень полезной мерой.

Пусть, например, задача состоит в том, чтобы, зная лишь некоторые ограничения на случайную величину (типа моментов, пределов области возможных значений и т.п.), задать для дальнейшего (каких-то расчетов или моделирования) конкретное распределение. Один из подходов к решению этой задачи дает «принцип максимума энтропии»: из всех распределений, отвечающих данным ограничениям, следует выбирать то, которое обладает максимальной дифференциальной энтропией. Смысл этого критерия состоит в том, что, выбирая максимальное по энтропии распределение, мы гарантируем наибольшую неопределенность, связанную с ним, т.е. имеем дело с наихудшим случаем при данных условиях.

Фундаментальное свойство энтропии случайного процесса

Особое значение энтропия приобретает в связи с тем, что она связана с очень глубокими, фундаментальными свойствами случайных процессов. Покажем это на примере процесса с дискретным временем и дискретным конечным множеством возможных состояний.

Назовем каждое такое состояние «символом», множество возможных состояний — «алфавитом», их число m — «объемом алфавита». Число возможных последовательностей длины n, очевидно, равно mn. Появление конкретной последовательности можно рассматривать как реализацию одного из mn возможных событий. Зная вероятности символов и условные вероятности появление следующего символа, если известен предыдущий (в случае их зависимости), можно вычислить вероятность P(C) для каждой последовательности С. Тогда энтропия множества , по определению, равна

Математическое ожидание этой функции

Это соотношение является одним из проявлений более общего свойства дискретных эргодических процессов. Оказывается, что не только математическое ожидание величины f_n(C) при n стремящемся к бесконечности имеет своим пределом H, но и сама эта величина f_n(C) стремится к H при n стремящемся к бесконечности. Другими словами, как бы малы ни были e > 0 и s > 0, при достаточно большом n справедливо неравенство

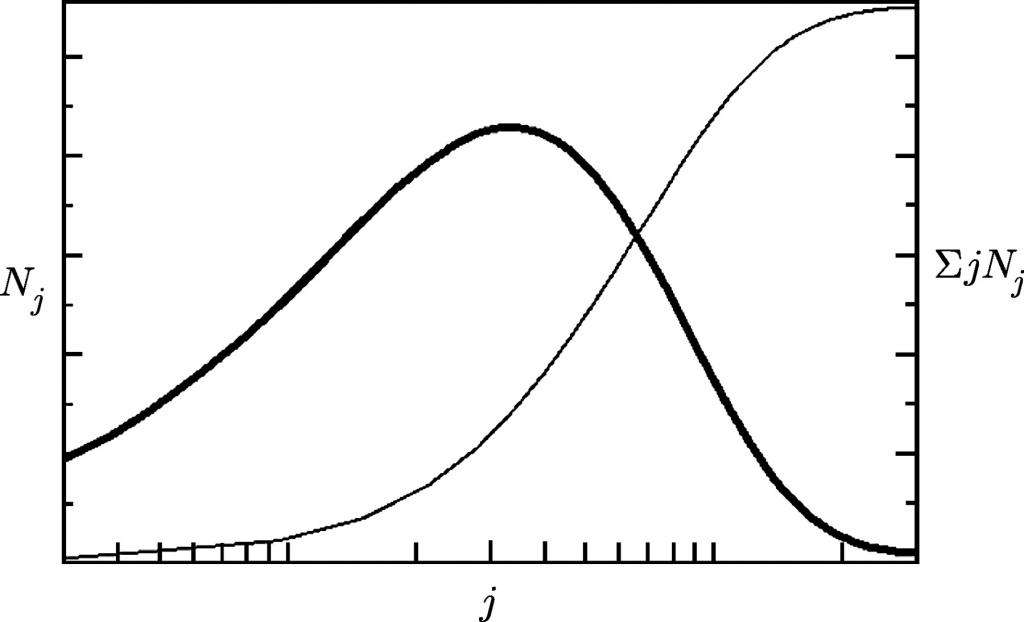
P <|[1/n]⋅log(P(C))+H| >ε> 0 и s > 0 можно найти такое no, что реализация любой длины n > no распадаются на два класса:

Число N всех возможных реализаций есть

Доля реализаций высоковероятной группы в общем числе реализаций выражается формулой

т.е. к высоковероятной группе относится лишь одна тридцати миллионная доля всех реализаций!

Строгое доказательство фундаментального свойства эргодических процессов здесь не приводится. Однако следует отметить, что в простейшем случае независимости символов это свойство является следствием закона больших чисел. Действительно, закон больших чисел утверждает, что с вероятностью, близкой к 1, в длиной реализации i-й символ, имеющий вероятность p_i встретится примерно np_i раз. Следовательно вероятность реализации высоковероятной группы есть

что и доказывает справедливость фундаментального свойства в этом случае.

Подведем итог

Связав понятие неопределенности дискретной величины с распределением вероятности по возможным состояниям и потребовав некоторых естественных свойств от количественной меры неопределенности, мы приходим к выводу, что такой мерой может служить только функционал (1), названный энтропией. С некоторыми трудностями энтропийный подход удалось обобщить на непрерывные случайные величины (введением дифференциальной энтропии) и на дискретные случайные процессы.

Количество информации

В основе всей теории информации лежит открытие, что «информация допускает количественную оценку». В простейшей форме эта идея была выдвинута еще в 1928г. Хартли, но завершенный и общий вид придал ее Шэннон в 1948г. Не останавливаясь на том, как развивалось и обобщалось понятие количества информации, дадим сразу ее современное толкование.

Количество информации как мера снятой неопределенности

Процесс получения информации можно интерпретировать как «изменение неопределенности в результате приема сигнала». Проиллюстрируем эту идею на примере достаточно простого случая, когда передача сигнала происходит при следующих условиях:

Итак, до получения очередного символа ситуация характеризуется неопределенностью того, какой символ будет отправлен, т.е. априорной энтропией Н(Х). После получения символа y_k неопределенность относительно того, какой символ был отправлен, меняется: в случае отсутствия шума она вообще исчезает (апостериорная энтропия равна нулю, поскольку точно известно, что был передан символ y_k=x_i), а при наличии шума мы не можем быть уверены, что принятый символ и есть переданный, т.е. возникает неопределенность, характеризуемая апостериорной энтропией H(X/y_k)=H(i/y_k)>)>0.

В среднем после получения очередного символа энтропия H(X/Y)=M_yk)>

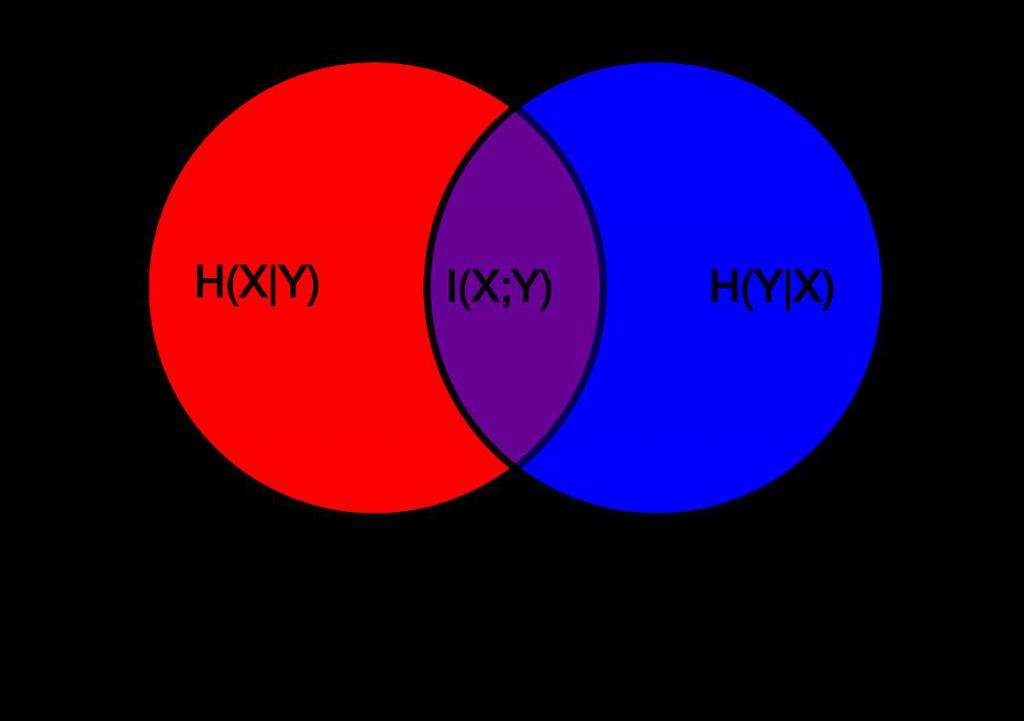
Определим теперь количество информации как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропии этого объекта, т.е. I(X,Y) = H(X)-H(X/Y). (1)

Используя свойство 2 энтропии, легко получить, что I(X,Y) = H(Y) — H(Y/X) (2)

В явной форме равенство (1) запишется так:

а для равенства (2) имеем:

Количество информации как мера соответствия случайных процессов

Представленным формулам легко придать полную симметричность: умножив и разделив логарифмируемое выражение в (3) на p(y_k), а в (4) на p(x_i) сразу получим, что

Эту симметрию можно интерпретировать так: «количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соответствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: «среднее количество информации, вычисляемое по формуле (5), есть мера соответствия двух случайных объектов».

Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Подчеркнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отражение есть результат взаимодействия, т.е. взаимного, обоюдного изменения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой — как следствие; это никак не учитывается при введенном количественном описании информации.

Формула (5) обобщается на непрерывные случайные величины, если в отношении (1) и (2) вместо Н подставить дифференциальную энтропию h; при этом исчезает зависимость от стандарта К и, значит, количество информации в непрерывном случае является столь же безотносительным к единицам измерения, как и в дискретном:

где р(x), p(y) и p(x,y) — соответствующие плотности вероятностей.

Свойства количества информации

Отметим некоторые важные свойства количества информации.

Источник