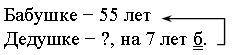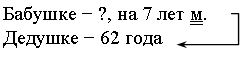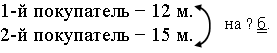Искомое число в задаче что это
Тема: Данные и искомое. Их выделение в тексте задачи
Тема: Данные и искомое. Их выделение в тексте задачи.
· дать понятие о данных и искомом задачи, учить выделять эти компоненты в тексте;
· закрепить знания приемов сложения и вычитания однозначных и двузначных чисел;
· развивать грамотную математическую речь, умение мыслить логически грамотно.
· воспитывать познавательный интерес к математике, умение сотрудничать.
Оборудование: учебник 2 класс 1 ч., рабочая тетрадь, карточки, презентация.
1. Организационная часть
¾ Долгожданный дан звонок
¾ Ребята, к нам на урок пришли гости, поздоровайтесь с ними. Улыбнитесь друг другу и мне.
2. Актуализация опорных знаний.
1.Работа с геометрическими фигурами (Приложение1)
¾ Посмотрите на экран:
¾ Какие геометрические фигуры видите? (прямоугольники, квадраты, круги, угол, треугольник)
¾ Что можете сказать о треугольнике?
¾ На какие 3 группы можно разделить все треугольники? (прямоугольные, остроугольные и тупоугольные)
¾ Назовите треугольники, объясните, почему они так называются. (На доске 3 вида треугольников)
¾ Молодцы, ребята. Вот на таком транспортном средстве мы отправляемся в путешествие по городу Математике. Пристегните ремни.
(Вагончик из геометрических фигур)
¾ Открываем тетрадь. Записываем число, классная работа.
¾ Я тетрадочку открою
Я, друзья, от вас не скрою
Ручку я вот так держу.
¾ Математика пришла, занимай свои места
Найди для головы полезное занятие
Чтоб от безделья не зевать,
Полезно голову ломать.
¾ Ребята, перед отправлением в путь, нужна разминка. Как известно, математика – это гимнастика ума.
2. Математический диктант.
¾ Уменьшаемое 48, вычитаемое 40. Найти значение разности.
¾ Увеличить 50 на 20.
¾ На сколько 62 больше 60?
¾ Найти сумму чисел 39 и 1.
¾ За тетрадку Михаил 10 рублей заплатил
А за пенал 50 рублей отдал
Сколько денег заплатил
За покупку Михаил? (30 + 50= 80)
¾ Привела гусыня мать
16 ребяток на луг гулять
Все гусята как клубочки
10 сыночков, а сколько дочек?(16-10=6)
Проверка : 8 80 70 2 40 60 6
¾ На какие 2 группы можно разделить числа?
¾ Назовите числа в порядке возрастания.
– Молодцы! Правильно владеете действиями и их компонентами.
3. Работа по теме урока.
¾ Ворота открыты, и наш путь лежит прямо по проспекту Задач.
Мы делаем первую остановку.
1. Работа с учебником: с.69, задача 145.
¾ Расставьте в правильном порядке составные части задачи:
Условие – то, что известно
Вопрос – то, что спрашивается
Решение – как ответить на вопрос
Ответ – сколько получится
¾ Молодцы! Вы все правильно выполнили. Но Мудрая Сова приготовила для вас новую информацию. А вот что? Мы сейчас и узнаем.
Ученик читает задачу.
Как называются эти числа? ( данными).
¾ Какое число в задаче нужно найти? Число, которое нужно найти, чтобы ответить на вопрос задачи, называют искомым.
 |  |
¾ Прочитайте вопрос задачи.
¾ Какие данные нужно знать, чтобы ответить на вопрос задачи? (сколько было тигрят, сколько было львят)
¾ Сколько было тигрят? (6)
¾ Сколько было львят? (9)
¾ Зная данные, мы можем ответить на вопрос задачи? (да)
¾ Сделайте схематичный рисунок к задаче.
Решение задачи с комментированием.
¾ Вы ответили на вопрос задачи? Подчеркните искомое.
¾ В какой части задачи содержится данные?
¾ Какую новую информацию приготовила для вас Сова? (Данные и искомое.)
¾ Это и есть тема нашего урока. Мы должны научиться выделять данные и искомое в тексте задачи
2. Самостоятельная работа.
1) по карточкам – по вариантам (Приложение 2)
2) Групповая работа. Составление задачи по данным.
– Молодцы! Вы отлично справились с заданием, а теперь пора отдохнуть.
Раз нагнулся, два нагнулся.
Руки в стороны развел,
Видно ключик не нашел.
Чтобы ключик нам достать,
На носочки надо встать.
Физминутка для глаз.
4. Работа над пройденным материалом.
¾ Продолжаем путь. Мы на аллее Плюсов и Минусов.
1. Запись на экране: 42 + 16= (40 +2)+ (10+6)= (40+10) +(2+6)=50+6=56
¾ Какими суммами заменили слагаемые?
¾ Как такие суммы называются?
¾ Как удобно выполнить счет?
¾ Какой вывод можно сделать?
Вывод: при сложении чисел удобно складывать десятки с десятками, а единицы с единицами.
2. Работа с № 000 с. 70 (комментирование)
Самостоятельно № 000 (3). Взаимопроверка.
¾ Значение какой суммы было найти легче остальных? (56+30 )
¾ Почему? (не надо заменять второе слагаемое суммой разрядных слагаемых)
¾ Назовите несколько таких сумм.
¾ Продолжая путешествие по городу Математике, побываем на улице Неравенств.
3. Работа с учебником № 000
¾ Найдите сходство в выражениях.
¾ Не выполняя вычисления поставьте знак сравнения.
5.Впереди перекресток Геометрический.
1 задание: начерти отрезок 1дм 1см. Запиши его длину в см.
2 задание: по вариантам:
Проверка выполнения задания «цепочкой»
¾ Подумай, все ли равенства верны. Если есть ошибки, исправь.
Урок математики во 2-м классе по теме “Данные и искомые. Их выделение в тексте задачи”
Тема: Данные и искомое. Их выделение в тексте задачи
.
Цель: Ввести понятия о данных и искомом задачи, учить выделять эти компоненты в тексте.
Оборудование: учебник 2 класс 1 ч., рабочая тетрадь, тетрадь на печатной основе 2 ч., веер цифр, геометрические фигуры.(3 вида треугольников), таблицы состава задачи, рисунок города «математики», название улиц, сигнальные карточки.
Ход урока
1. Организационная часть
Долгожданный дан звонок
Начинается урок.
– Ребята, к нам на урок пришли гости, поздоровайтесь с ними. Улыбнитесь друг другу и мне.(сигнал настроения)
2. Посмотрите на доску:
– Какие геометрические фигуры видите? (прямоугольники, квадраты, круги, угол, треугольник)
– Что можете сказать о треугольнике?
– На какие 3 группы можно разделить все треугольники? (прямоугольные, остроугольные и тупоугольные)
– Назовите треугольники, объясните, почему они так называются. (На доске 3 вида треугольников)
– Молодцы, ребята. Вот на таком транспортном средстве мы отправляемся в путешествие по городу Математике. Пристегните ремни.
(Картина города Математики)
Математика пришла, занимай свои места
Найди для головы полезное занятие
Чтоб от безделья не зевать,
Полезно голову ломать.
– Ребята, перед отправлением в путь нужна разминка. Как известно, математика – это гимнастика ума.
3 Устный счет. Работа с веером цифр.
За тетрадку Михаил 30 рублей заплатил
А за пенал 50 рублей отдал
Сколько денег заплатил
За покупку Михаил? (30 + 50= 80)
) Лебеди у нас в пруду
Я поближе подойду
9 черных, белых – 5
Кто успел их сосчитать?
Покажи поскорей
Сколько было лебедей? (9+5=14)
Привела гусыня мать
16 ребяток на луг гулять
Все гусята как клубочки
10 сыночков, а сколько дочек?(16-10=6)
(Оценки за устный счет)
4. Ворота открыты, и наш путь лежит прямо по проспекту задач.
Мы делаем первую остановку.
Открываем тетрадочки. Записываем число, классная работа.
Я тетрадочку открою
И как надо положу.
Я, друзья от вас не скрою,
Ручку правильно держу.
5. Работа по теме урока.
Работа с учебником: с.69, задача 145.
Расставьте в правильном порядке составные части задачи:
Условие – то, что известно
Вопрос – то, что спрашивается
Решение – как ответить на вопрос
Ответ – сколько получится
Молодцы! Вы все правильно выполнили. Но Мудрая Сова приготовила для вас новую информацию. А вот что, мы сейчас и узнаем.
-А теперь придумайте свою задачу.
(Выслушать придуманные детьми 2-3 задачи. Выделить в них данные и искомое. )
Оценки за составление задач.
– Молодцы! Вы отлично справились с заданием, а теперь пора отдохнуть. ( Картинка Буратино)
Буратино потянулся,
Раз нагнулся, два нагнулся.
Руки в стороны развел,
Видно ключик не нашел.
Чтобы ключик нам достать,
На носочки надо встать.
6. Работа над пройденным материалом.
Продолжаем путь. Мы на аллее Плюсов и Минусов.
Запись на доске: 34 + 42= (30 +4)+ (40+2)= (30+40) +(4+2)=70+6=76
– Ответь на вопросы:
– Какими суммами заменили слагаемые?
– Как такие суммы называются?
Вывод: при сложении чисел удобно складывать десятки с десятками, а единицы с единицами.
Самостоятельная работа № 146.
Дозированная помощь учащимся на карточках:
1.Замени числа суммой разрядных слагаемых:
2.Сложи десятки:50+20
3.Сложи единицы: 6+3
4. Выполни сложение десятков и единиц
– Значение какой суммы было найти легче остальных? (56+30 )
– Почему? (не надо заменять второе слагаемое на сумму разрядных слагаемых)
В домашней работе вы запишите 5 таких сумм.
Взаимопроверка самостоятельной работы.
7.Впереди перекресток Геометрический.
1 задание: начерти отрезок 1дм 1см. Запиши его длину в см.
2 задание: по вариантам:
Проверка выполнения задания «цепочкой»
1 дм 8см = 81см
80 дм =8 см
73 см = 7дм 3см
Подумай, все ли равенства верны. Если есть ошибки, исправь.
Оценки за выполненную работу.
8. Продолжая путешествие по городу Математике, побываем на улице Неравенств.
Работа с учебником № 148
– Объясните постановку знаков сравнения:
2 строчка – самостоятельная работа
Устная проверка работы.
– Закончилось путешествие по городу.
– Что нового узнали?
Оценки за работу на уроке.
Всем спасибо!
Данные и искомое. Их выделение в тексте задачи. 2 класс
Тема: Данные и искомое. Их выделение в тексте задачи.
Цель:
• дать понятие о данных и искомом задачи, учить выделять эти компоненты в тексте;
• закрепить знания приемов сложения и вычитания однозначных и двузначных чисел;
• развивать грамотную математическую речь, умение мыслить логически грамотно.
• воспитывать познавательный интерес к математике, умение сотрудничать.
Открытый урок математики во 2 классе по теме « Данные и искомое. Их выделение в тексте задачи»
Учитель: Ефлаева Ф.Ш.
Тема: Данные и искомое. Их выделение в тексте задачи.
дать понятие о данных и искомом задачи, учить выделять эти компоненты в тексте;
закрепить знания приемов сложения и вычитания однозначных и двузначных чисел;
развивать грамотную математическую речь, умение мыслить логически грамотно.
воспитывать познавательный интерес к математике, умение сотрудничать.
Оборудование: учебник 2 класс 1 ч., рабочая тетрадь, карточки, презентация.
1. Организационная часть
Долгожданный дан звонок
Ребята, к нам на урок пришли гости, поздоровайтесь с ними. Улыбнитесь друг другу и мне.
2. Актуализация опорных знаний.
1.Работа с геометрическими фигурами (Приложение1)
Посмотрите на экран:
Какие геометрические фигуры видите? (прямоугольники, квадраты, круги, угол, треугольник)
Что можете сказать о треугольнике?
На какие 3 группы можно разделить все треугольники? (прямоугольные, остроугольные и тупоугольные)
Назовите треугольники, объясните, почему они так называются. (На доске 3 вида треугольников)
Молодцы, ребята. Вот на таком транспортном средстве мы отправляемся в путешествие по городу Математике. Пристегните ремни.
(Вагончик из геометрических фигур)
Открываем тетрадь. Записываем число, классная работа.
Я тетрадочку открою
Я, друзья, от вас не скрою
Ручку я вот так держу.
Математика пришла, занимай свои места
Найди для головы полезное занятие
Чтоб от безделья не зевать,
Полезно голову ломать.
Ребята, перед отправлением в путь, нужна разминка. Как известно, математика – это гимнастика ума.
2. Математический диктант.
Уменьшаемое 48, вычитаемое 40. Найти значение разности.
Увеличить 50 на 20.
На сколько 62 больше 60?
Найти сумму чисел 39 и 1.
За тетрадку Михаил 10 рублей заплатил
А за пенал 50 рублей отдал
Сколько денег заплатил
За покупку Михаил? (30 + 50= 80)
Привела гусыня мать
16 ребяток на луг гулять
Все гусята как клубочки
10 сыночков, а сколько дочек?(16-10=6)
Проверка : 8 80 70 2 40 60 6
На какие 2 группы можно разделить числа?
Назовите числа в порядке возрастания.
– Молодцы! Правильно владеете действиями и их компонентами.
3. Работа по теме урока.
Ворота открыты, и наш путь лежит прямо по проспекту Задач.
Мы делаем первую остановку.
1. Работа с учебником: с.69, задача 145.
Расставьте в правильном порядке составные части задачи:
Условие – то, что известно
Вопрос – то, что спрашивается
Решение – как ответить на вопрос
Ответ – сколько получится
Молодцы! Вы все правильно выполнили. Но Мудрая Сова приготовила для вас новую информацию. А вот что? Мы сейчас и узнаем.
Ученик читает задачу.
Как называются эти числа? ( данными).
Какое число в задаче нужно найти? Число, которое нужно найти, чтобы ответить на вопрос задачи, называют искомым.
Прочитайте вопрос задачи.
Какие данные нужно знать, чтобы ответить на вопрос задачи? (сколько было тигрят, сколько было львят)
Сколько было тигрят? (6)
Сколько было львят? (9)
Зная данные, мы можем ответить на вопрос задачи? (да)
Сделайте схематичный рисунок к задаче.
Решение задачи с комментированием.
Вы ответили на вопрос задачи? Подчеркните искомое.
В какой части задачи содержится данные?
Какую новую информацию приготовила для вас Сова? (Данные и искомое.)
Это и есть тема нашего урока. Мы должны научиться выделять данные и искомое в тексте задачи
2. Самостоятельная работа.
по карточкам – по вариантам (Приложение 2)
Групповая работа. Составление задачи по данным.
– Молодцы! Вы отлично справились с заданием, а теперь пора отдохнуть.
Раз нагнулся, два нагнулся.
Руки в стороны развел,
Видно ключик не нашел.
Чтобы ключик нам достать,
На носочки надо встать.
Физминутка для глаз.
4. Работа над пройденным материалом.
Продолжаем путь. Мы на аллее Плюсов и Минусов.
1. Запись на экране: 42 + 16= (40 +2)+ (10+6)= (40+10) +(2+6)=50+6=56
Какими суммами заменили слагаемые?
Как такие суммы называются?
Как удобно выполнить счет?
Какой вывод можно сделать?
Вывод: при сложении чисел удобно складывать десятки с десятками, а единицы с единицами.
2. Работа с № 146 с. 70 (комментирование)
Самостоятельно № 146 (3). Взаимопроверка.
Значение какой суммы было найти легче остальных? (56+30 )
Почему? (не надо заменять второе слагаемое суммой разрядных слагаемых)
Назовите несколько таких сумм.
Продолжая путешествие по городу Математике, побываем на улицеНеравенств.
3. Работа с учебником № 148
Найдите сходство в выражениях.
Не выполняя вычисления поставьте знак сравнения.
5.Впереди перекресток Геометрический.
1 задание: начерти отрезок 1дм 1см. Запиши его длину в см.
2 задание: по вариантам:
Проверка выполнения задания «цепочкой»
Подумай, все ли равенства верны. Если есть ошибки, исправь.
Данные и искомое
Конспект урока по теме “Данные и искомое”, цели которого: ввести эти понятия, совершенствовать умения составлять задачу, развивать логическое мышление.
Просмотр содержимого документа
«Данные и искомое»
Цели: ввести понятия «данные» и «искомые»; совершенствовать умение составлять задачу; формировать умение решать задачи; развивать логическое мышление.
I. Организационный момент.
II. Введение в тему урока.
– Прочитайте задачу. Назовите данные из условия.
– Что является искомым в этой задаче?
– Вычислите искомое по двум данным.
62 – 55 = 7 (лет) – старше.
О т в е т: на 7 лет старше.
– Прочитайте задачу. Назовите данные из условия.
– Что является искомым в этой задаче?
– Вычислите искомое по двум данным.
55 + 7 = 62 (года) – дедушке.
Ответ: дедушке 62 года.
– Составьте две задачи так, чтобы данное из первой задачи стало искомым во второй.
III. Поупражняемся в вычислениях.
Учащиеся составляют задачи.
1-й покупатель – 12 м.
2-й покупатель – 15 м.
– Прочитайте задачу. Назовите данные. Все ли данные нужны для того, чтобы ответить на требование?
– Данное о том, что в третьем мешке 33 кг моркови, нам не потребовалось. Это лишнее данное.
Урок 19 Бесплатно Нахождение числа по его дроби
В этом уроке мы научимся, зная дробь от числа, находить все число.
Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.
Потом применим полученные навыки для решения задач.
Нахождение числа по его дроби
Сформулируем, в чем состоит задача нахождения числа по его дроби.
Имеется дробь; она говорит о том, какая часть от числа нам дана.
Имеется число, равное данной дробной части от искомого числа.
Мы уже умеем находить дробь от числа. Вспомним как это делать.
Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.
В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.
В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.
Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.
Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.
Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.
Итак, вы получили выражение для неизвестного числа.
Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.
Пример 1
\(\mathbf<\frac<3><4>>\) от числа равны 21-му, найдите исходное число.
Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на \(\mathbf<\frac<3><4>>\)
Пример 2
\(\mathbf<\frac<2><7>>\) от числа равны 12, найдите исходное число.
Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на \(\mathbf<\frac<2><7>>\)
Пример 3
Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.
\(\mathbf<\frac<2><3>>\) от числа равны 11, найдите исходное число.
Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную \(\mathbf<\frac<2><3>>\), на величину дроби, равную 11 и получим результат.
Для получения ответа нам понадобилось выделить целую часть.
Важен еще один случай.
Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.
Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.
Пример 4
\(\mathbf<\frac<5><6>>\) от числа равны \(\mathbf<\frac<2><3>>\), найдите все число.
Для решения этого примера разделим \(\mathbf<\frac<2><3>>\)- часть числа, на \(\mathbf<\frac<5><6>>\)- дробь.
Все исходное число равняется \(\mathbf<\frac<4><5>>\)
Пройти тест и получить оценку можно после входа или регистрации
Нахождение числа по проценту
Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.
Вспомним, что процент- это способ записи десятичной дроби.
То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.
Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.
Пример 1
Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?
Решение:
Переведем проценты в дроби: \(\mathbf<25\%=25\div100=0.25>\)
Разделим число на дробь: \(\mathbf<2000\div0.25=8000>\)
Ответ: изначально зарплата работника была 8000 рублей.
Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.
Пример 2
Сказано, что 9% от числа равны 81. Необходимо найти все число.
Решение:
Первым действием переводим проценты в десятичную дробь.
Вторым действием делим данное число на эту дробь.
Ответ: искомое число 900
Пройти тест и получить оценку можно после входа или регистрации
Решение задач на дроби от числа и проценты
Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.
Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.
Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.
Пример:
Айсберг возвышается над водой на \(\mathbf<\frac<1><11>>\) своей высоты.
Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.
Какова общая высота айсберга?
Решение:
В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- \(\mathbf<\frac<1><11>>\).
Соответственно, по правилу, для получения ответа мы делим 16 на \(\mathbf<\frac<1><11>>\) и получаем результат.
\(\mathbf<16\div\frac<1><11>=16\cdot11=176>\) (метр)- общая высота айсберга
Ответ: 176 (метров).
Некоторые задачи для своего решения требуют более глубокого анализа.
Пример:
Магазин продал \(\mathbf<\frac<2><3>>\) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.
Какого размера была специальная партия?
Решение:
В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на \(\mathbf<\frac<2><3>>\) и получить ответ, но ответ не будет правильным.
Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь \(\mathbf<\frac<2><3>>\) описывает проданную часть.
Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует \(\mathbf<\frac<2><3>>\)
Зато мы можем вычислить размер оставшейся части.
Эта дробь соответствует 56 оставшимся парам.
Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.
Теперь оформим решение:
1) \(\mathbf<1-\frac<2><3>=\frac<1><3>>\) составляет оставшаяся часть от всего размера партии
2) \(\mathbf<56\div\frac<1><3>=56\cdot3=168>\) (пар) кроссовок всего было в партии
Ответ: 168 (пар).
Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Задачи математики часто диктуются другими науками, в том числе экономикой.
Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.
Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.
В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.
Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.
К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.
В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.
К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.
Именно в этот период математика начала активно применяться в экономике.
В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.
Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации