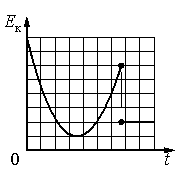
Используя данные рисунка и учитывая что представленный график имеет вид параболы
Тест №5 ЕГЭ по физике
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
Алгоритм решения
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
а) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.
б) Тело брошено под углом к горизонту с поверхности Земли и упало на Землю.
в) Тело брошено под углом к горизонту с поверхности Земли и упало на балкон.
г) Тело брошено вертикально вверх с балкона и упало на Землю.
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=”671″ src=”https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=”602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Используя данные рисунка и учитывая что представленный график имеет вид параболы
По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)
Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале времени от 0 до 2 с автомобиль прошёл путь
Примечание. В принципе, интересующий нас участок (от 0 до 2 с) не обязательно разбивать на два, площадь под графиком можно посчитать, как площадь трапеции:
В принципе, можно использовать стандартные кинематические формулы для изменения координаты, скорости, ускорения, а все необходимые данные снимать с графика. Но так получается значительно дольше.
Почему же не через площадь дольше?
S= So + vt + (at^2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;
Правильно. Так тоже можно.
В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.
В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂
Утверждение “в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)” не совсем верно, правильно тогда уж говорить так: “за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с”.
Однако такое утверждение в свою очередь требует разъяснений.
так путь же нужно найти почему нельзя воспользоваться формулой S=Vt
Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется
В задании не сказано, но тело двигалось прямолинейно
Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.
На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)
Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь
Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.
Задания ОГЭ на анализ графиков
Часть I
Узнайте, как можно поддержать сайт и помочь его развитию.
Изученные функции и их графики.
К концу учебного года в 9-ом классе вы успели изучить следующие функции:
Ещё подробнее повторить графики функций вы сможете, если перейдёте к сводной таблице и воспользуетесь помещенными там ссылками на другие статьи сайта и видео на youtube-канале Mathematichka.
Задания на соответствие графика и формулы функции.
Задачи, в которых приведены графики функций разных типов, я считаю самыми лёгкими в этом задании. Давайте рассмотрим несколько примеров, и вы в этом убедитесь.
Задача 1. Установите соответствие между графиками функций и формулами, которые их задают
На рисунке всего один график прямая линия. Ищем среди формул ту, которая содержит \(x\) только в первой степени. Смотрим, чтобы в этой формуле не было квадрата и переменной в знаменателе. Такая формула только одна, это формула \(3)\; y=-2x\). Делаем вывод: графику Б) соответствует формула 3).
Среди формул только одна содержит \(x^2\) (формула 4), и только один график непрерывная кривая линия симметричная относительно вертикальной прямой, проведенной через её вершину. Это парабола – график В). Вывод: графику В) соответствует формула 4).
Ответ:
| А | Б | В |
| 1 | 3 | 4 |
Ответы и решения некоторых задач временно скрыты. Это задачи для самостоятельного решения. Чтобы посмотреть ответы, воспользуйтесь соответствующими кнопками. Но предварительно попробуйте решить задачу самостоятельно.
Задача 2. Установите соответствие между функциями и их графиками.
На графике 1) линия с разрывом, следовательно в формуле есть \(x\) в знаменателе. Вывод: графику 1) соответствует формула А).
На графике 2) изображена прямая линия. Осталась только одна формула, где \(x\) в первой степени умножен на число \(\dfrac<3x> <2>= \dfrac<3><2>\cdot x\). Вывод: графику 2) соответствует формула В).
Два оставшихся графика нелинейны, т.е. кривые линии. Формула Б) представляет собой квадратный трёхчлен. Следовательно, график должен быть параболой. Мы знаем, что парабола симметрична относительно линии, проходящей через вершину. График 3) обладает этим свойством, а на графике 4) такую линию провести невозможно. Вывод: формула Б) соответствует графику 3).
Замечение. Проверку ответа можно сделать “по единичке”, т.е. задать какое-либо значение \(x\), подставить его в формулы, вычислить значения \(y\) и найти соответствующие точки на графике. Но решить задание в буквальном смысле по единичке, т.е. подставить \(x = 1\) в формулу Б), а затем найти на графиках 3) и 4) ординаты точек с абсциссой 1, не получится. Потому что во всех случаях будет \(y = 2\). Выбор не состоится.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Задача 3. Установите соответствие между графиками функций и формулами, которые их задают.
Координатные плоскости здесь представлены без клеточек. Проверить принадлежность точек не получится, выбираем только по внешнему виду графиков.
Прямая линия олна – А). Её формула 1) содержит просто \(x\).
Симметричная кривая на графике В) – парабола. Формула 2) содержит \(x^2\).
На среднем графике кривая линия похожа на перевёрнутую половинку параболы. Это график функции 3) квадратный корень.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Линейная функция. Прямая линия.
Задача 4. Установите соответствие между графиками функций и формулами, которые их задают.
Все графики – прямые линии и все формулы имеют вид \(y = kx + b\). Выбираем по наклону к оси \(Ox\) и точке пересечения с осью \(Oy\).
На графике В) прямая никак не наклонена к оси \(Ox\), она ей параллельна. Следовательно, угол наклона равен 0, тангенс угла наклона равен 0, угловой коэффициент \(k=0\), и \(y = kx + b = 0\cdot x + b = 0 + b = b.\) Таким образом, формула, которая задаёт прямую, параллельную оси абсцисс, не должна содержать \(x\). Здесь такая формула под номером 3.
В двух оставшихся графиках наклон на глаз кажется примерно одинаковым. Поэтому начнём с точки пересечения с с осью \(Oy\). Вспомним, что для точек, расположенных на этой оси, \(x=0\), поэтому \(y = kx + b = k\cdot0 + b = 0 + b = b.\) Таким образом, высота точки пересечения графика с этой осью показывает значение коэффициента \(b\) в формуле функции. На первом графике пересечение при \(y=2\), подходит формула \(2)\; y = x+2.\) На втором – при \(y=0\), подходит формула \(1)\; y = 2x,\) так как \(2x = 2x+0.\)
Сделаем проверку по единичке для графиков А) и Б).
При \(x=1\) по формуле 2) получим \(y = 1 + 2 = 3\). Если мы правильно установили соответствие, то точка с координатами (1;3) должна лежать на графике А).
При \(x=1\) по формуле 1) получим \(y = 2\cdot1 =2\). Если мы правильно установили соответствие, то точка с координатами (1;2) должна лежать на графике Б).
Отметим эти точки на указанных графиках. Точки “не промахнулись”, значит задача решена верно.
Ответ:
| А | Б | В |
| 2 | 1 | 3 |
Итак, все графики, которые задаются формулой \(y = b\), т.е. формулой, содержащей \(y\) и число, но не содержащей \(x\), представляют собой прямые линии, параллельные оси \(Ox\). Все графики, которые задаются формулой \(y = kx\), т.е. формулой, содержащей \(x\) в виде одночлена первой степени, представляют собой прямые линии, проходящие через начало координат. Эти выводы нужно запомнить на будущее не только, чтобы быстрее решать это задание ОГЭ, но и для задания на графики во второй части экзаменационного варианта.
Задача 5. Установите соответствие между функциями и их графиками.
Прямые на графиках 1) и 2) имеют одинаковый наклон. Одинаковый угловой коэффициент \(k = 2\) мы видим в формулах Б) и В). Методом исключения делаем вывод, что для графика 3) остаётся формула А).
Ответ:
| А | Б | В |
| 3 | 1 | 2 |
Задача 6. На рисунке изображены графики функций вида \(y = kx+b.\) Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
Угловой коэффициент равен тангенсу угла наклона прямой к оси \(Ox.\) На данный момент мы знаем, что тангенс определён в прямоугольном треугольнике, как отношение противолежащего катета к прилежащему. Поэтому, прежде всего, надо начертить прямоугольные треугольники такие, что их гипотенузы лежат на заданных прямых, а катеты проходят по клеточкам. Вершины этих треугольников обязательно должны находиться в узлах клеточек, иначе будет трудно определить длины катетов. Размер треугольника может быть произвольным, “приклеить” его к прямой можно в любом удобном месте.
Угол наклона прямой по определению отсчитывается от положительного направления оси абсцисс (оси \(Ox\)), поэтому в наших треугольниках противолежащий катет всегда параллелен оси \(Oy\) (считаем клеточки по вертикали), а прилежащий – оси \(Ox\) (считаем клеточки по горизонтали).
Если прямая образует с положительным направлением оси абсцисс тупой угол, то угловой коэффициент будет со знаком минус. Поскольку линии клеток параллельны, то можно смотреть угол между прямой и правой частью горизонтальных линий сетки, как показано на рисунке.
Итак, вычисляем угловые коэффициенты по чертежу
Ответ:
| А | Б | В | Г |
| 4 | 2 | 3 | 1 |
На эту тему также можно посмотреть видеоуроки на странице Линейная функция или на youtube-канале Mathematichka.
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:


















































