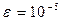Итерационные циклы что это

Итерационные циклы.

Если число повторений заранее не известно и решение о завершении цикла принимается на основе анализа некоторого условия, то такой повторяющийся вычислительный процесс называется итерационным циклом.

Синтаксическая структура оператора цикла с предусловием имеет вид:

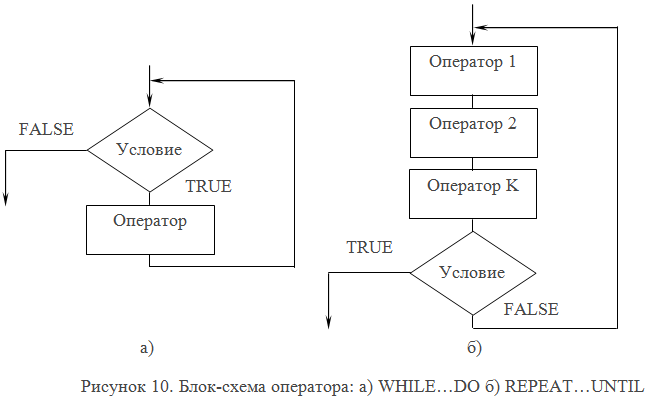
Как видно из блок-схемы (рисунок 10.а), перед каждым выполнением цикла анализируется логическое выражение или переменная. При значении TRUE выполняется оператор, составляющий тело цикла. При значении FALSE управление передается следующему за циклом оператору. Если условие ложно с самого начала, то оператор не выполняется ни разу.

Цикл с постусловием. Оператор REPEAT. UNTIL.

Break, Continue.

В циклах FOR, REPEAT, WHILE можно использовать процедуры BREAK и CONTINUE. Первая процедура позволяет досрочно выйти из цикла, не дожидаясь выполнения условий выхода. Вторая процедура позволяет начать новую итерацию цикла даже в том случае, если предыдущая итерация не завершена. Использование этих процедур ускоряет работу программы в рамках принципа структурного программирования.

Обозначение циклов на блок-схемах согласно ГОСТу.

ГОСТом предусмотрен единый блок для обозначения различных циклов (Рисунок 11). В блоке, соответствующем началу цикла указывается имя цикла (Как правило, это одна буква латинского алфавита) и начальное значение переменной цикла. В зависимости от оператора цикла, условие окончания записывается либо в блоке, соответствующем началу цикла (для операторов FOR…DO и WHILE…DO), либо в блоке, соответствующем концу цикла (для оператора REPEAT…UNTIL). Аналогично записывается и шаг изменения переменной цикла.

Источник

Итерационные циклы

Итерационными называют такие циклы, у которых заранее неизвестно количество шагов. С помощью итерационных циклов решаются задачи, использующие метод последовательных приближений.

Примером, использующим итерационный цикл, может быть следующая задача.

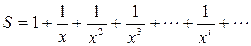
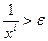
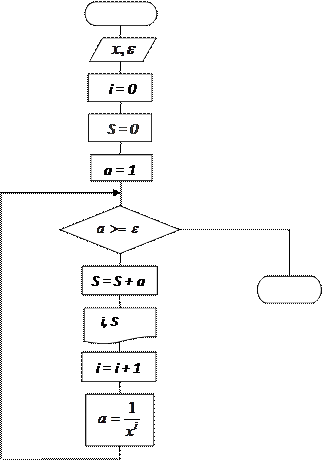Вычислить: сумму , для любых х > 1. Вычисление производить, пока .

Рис.8.6. Блок – схема итерационного цикла с предусловием

В итерационных циклах основанием для завершения их работы является некое условие. Если оно выполняется, то цикл работает, в противном случае цикл прекращает работу. В представленной задаче цикл работает до тех пор, пока условие 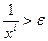выполняется. Итерационные циклы могут быть представлены с предусловием или с послеусловием. Циклы с предусловием предусматривают вначале проверку условия выполнения цикла, а затем, если условие выполняется, осуществляется выполнение тела цикла.

В циклах с послеусловием эта процедура производится в обратном порядке – сначала выполняется тело цикла, а после этого проверяется условие выполнения цикла. В этих циклах возможно выполнение один раз тела цикла даже тогда, когдаэто не должно происходить.Об этом становится известно уже после выполнения тела цикла. Казалось бы, что циклы с послеусловием бессмысленны, но существуют области задач, где их применение более предпочтительно.

На рис. 8.6 и 8.7 приведены блок – схемы вычислений с использованием циклов соответственно с предусловием и послеусловием.

+ –

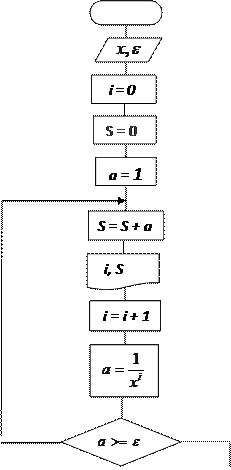Рис.8.7. Блок – схема итерационного цикла с послеусловием

Источник

Итерационные циклы что это

Итак, любой цикл как процесс можно охарактеризовать четырьмя составляющими:

· ограничение цикла (условие продолжения или завершения):

· переход к следующему шагу :

· повторяющееся действие – тело цикла.

В большинстве циклов действия, производимые в теле цикла, не влияют на параметры его протекания: количество шагов, характеристики шага. В таких «хороших» циклах параметры заголовка цикла не зависят от значений переменных, вычисляемых в теле цикла, и цикл имеет постоянное количество повторений, например:

Если же поведение программы на некотором шаге цикла может зависеть от результатов выполнения тела цикла на предыдуших шагах, либо число повторений цикла зависит от результатов выполнения шага, такие циклы и программируемые ими процессы называются итерационными. Наиболее широко они применяются в вычислительной математике, когда для получения численного результата используется итерационный цикл последовательных приближений к нему.

Если в итерационном цикле гарантируется выполнение одного шага, тo может быть использован цикл do. while.

x=. ; x1=. ; // Начальное значение текущего шага

x2 = x1; x1 = x; // Следующий шаг

x = …x1…x2…; // Результат текущего шага

> while (условие(x2,x1,x)); // Условие завершения

Если использовать результат только текущего шага, который зависит от результата предыдущего, то схему цикла можно упростить.

Рекуррентные последовательности

При прямом вычислении элементов последовательности необходимы три переменные для хранения текущего, предыдущего и «позавчерашнего» значений.

Fn2=Fn1; // Переход к следующему шагу:

Fn1=Fn; // текущий становится предыдущим

sin(nx) = sin((n-1)x)cos(x) + cos((n-1)x)sin(x)

//— sin, cos кратных углов

double Cn,Cn1,C0,Sn,Sn1,S0; // S0=sin(x), Sn1=sin((n-1)x), Sn=sin(nx)

Cn1=C0=cos(FI*pi/180); // при n=2 sin((n-1)x)=sin(x)

Sn = Sn 1* C 0 + Cn 1* S 0; // Рекуррентная формула

Cn1=Cn; // Переход к следующему шагу

Sn1=Sn; // текущий становится предыдущим

Приближенные вычисления

Пока что итерационные циклы давали нам «экономию вычислений», избавляя от повторения одних и тех же действий. В вычислительной математике работает другая идея. В методе последовательных приближений координаты очередной точки в пространстве поиска вычисляются через координаты предыдущих точек, а сама последовательность бесконечно приближается (сходится) к некоторой точке с заданным свойством. Число шагов цикла определяется точностью приближения к предельной точке, а оно, в свою очередь, оценивается расстоянием между текущей и предыдущей.

Сама идея, на каких принципах организовать движение от точки к точке, к программированию, как таковому, не относится. Она лежит в предметной области, откуда и ведутся все доказательства работоспособности метода. Для практического программирования важно следующее :

· число шагов цикла (скорость сходимости) определяется самим методом (функцией, вычисляющей следующую точку), а также начальной точкой;

· возможны случаи, когда процесс, наоборот, расходится, т.е. «уходит» от исходной точки, увеличивая значения координат до бесконечности (в программе – переполнение).

Рассмотрим простейший способ нахождения корня функции методом последовательных приближений Для того, чтобы найти корень функции f(x)=0, решается эквивалентное уравнение x = f(x) + x. Если в него подставить точное значение корня, то правая и левая части совпадут. Если же поставить в правую часть любое «постороннее» значение x 1, то в левой части получим значение, отличающееся от x 1, например x : x = f ( x 1)+ x 1.

рис. 43-1. Итерационный цикл приближенного решения уравнения

Источник

Программирование итерационного цикла

Вы будете перенаправлены на Автор24

Итерационный цикл — это цикл, количество повторов в котором определяется результатами вычислений в теле цикла, и оно заранее неизвестно.

Введение

Итерационным циклом является циклическая процедура, количество повторов в которой определяется результатами расчётов в теле цикла, и до конца расчётов его нельзя определить.

Итерационным циклом с точным решением является процесс вычислений, который позволяет достичь (или превысить) значение функции, подлежащее определению.

Итерационным циклом, дающим приближённое решение, является процесс вычислений, при котором достижение искомого значения функции не представляется возможным, а возможно лишь приближение с некоторой погрешностью.

Программирование итерационного цикла

Существуют следующие методы определения значения функции итерационного цикла:

При вычислении значения функции с применением аргумента, осуществляется вычисление текущего значения функции по формуле, равнозначной применяемой в арифметических циклах:

Принципиальным отличием является интервал значений, в котором меняется аргумент ($x_i$). Перед началом вычислений задаётся только его начальное значение:

Готовые работы на аналогичную тему

Стандартное правило, по которому изменяется аргумент, остаётся прежним, то есть

следует предписание, требующее определять последующие величины функции через предыдущие.

Возможны следующие варианты выполнения этого процесса вычислений:

Для первого варианта процесс движется к известной заранее (то есть достижимой) итоговой величине функции (yгр). То есть интервал изменений циклического параметра i определяется зависимостью:

Это означает, что процесс рекуррентных вычисления является точным.

В дополнение к приведённой классификации, возможно деление итерационных циклов по характеру результатов на:

Сходящимся итерационным циклом является процесс, в котором величины текущих компонентов, формирующих функцию, становятся меньше по модулю.

Расходящимся итерационным циклом является процесс, в котором величины текущих компонентов, формирующих функцию, возрастают по модулю. Следует заметить, что такие процессы считаются допустимыми только для итерационных циклов, имеющих точное решение.

Обязательным условием итерационных циклов, имеющих приближённое решение, является сходящийся вычислительный процесс.

Количество повторных выполнений итерационного цикла подчиняется выражению:

Рассмотрим пример формирования алгоритма, позволяющего вычислить бесконечную сумму:

Рисунок 1. Пример формирования алгоритма, позволяющего вычислить бесконечную сумму. Автор24 — интернет-биржа студенческих работ

Определение суммы является стандартной циклической задачей. Но данная задача отличается тем, что количество сложений, то есть количество повторных выполнений тела цикла, заранее не определено. По этой причине циклический процесс должен быть завершён при достижении необходимой точности. При формировании алгоритма следует учитывать чередование знаков слагаемых, и что степень символа x в числителе слагаемого непрерывно растёт.

Рисунок 2. Блок-схема алгоритма. Автор24 — интернет-биржа студенческих работ

Источник

Итерационные циклы что это

В большинстве задач, встречающихся на практике, необходимо производить многократное выполнение некоторого действия. Такой многократно повторяющийся участок вычислительного процесса называется циклом.

Если заранее известно количество необходимых повторений, то цикл называется арифметическим. Если же количество повторений заранее неизвестно, то говорят об итерационном цикле.

В итерационных циклах производится проверка некоторого условия, и в зависимости от результата этой проверки происходит либо выход из цикла, либо повторение выполнения тела цикла. Если проверка условия производится перед выполнением блока операторов, то такой итерационный цикл называется циклом с предусловием (цикл «пока»), а если проверка производится после выполнения тела цикла, то это цикл с постусловием (цикл «до»).

Особенность этих циклов заключается в том, что тело цикла с постусловием всегда выполняется хотя бы один раз, а тело цикла с предусловием может ни разу не выполниться. В зависимости от решаемой задачи необходимо использовать тот или иной вид итерационных циклов.

Арифметические циклы

Оператор for вызывает оператор, находящийся после слова do, по одному разу для каждого значения в диапазоне от значения 1 до значения 2.

Переменная цикла, начальное и конечное значения должны иметь порядковый тип. Со словом to, значение переменной цикла увеличивается на 1 при каждой итерации цикла. Со словом downto, значение переменной цикла уменьшается на 1 при каждой итерации цикла. Не следует самостоятельно изменять значение управляющей переменной внутри цикла.

Пример 1. Квадраты чисел от 2-х до 10-и.

Пример 2. Латинский алфавит.

Пример 3. Использование цикла с downto.

Пример 4. Использование составного оператора.

Итерационные циклы с предусловием

Оператор после do будет выполняться до тех пор, пока логическое выражение принимает истинное значение (True). Логическое выражение является условием возобновления цикла. Его истинность проверяется каждый раз перед очередным повторением оператора цикла, который будет выполняться лишь до тех пор, пока логическое выражение истинно. Как только логическое выражение принимает значение ложь (False), осуществляется переход к оператору, следующему за while.

Выражение оценивается до выполнения оператора, так что если оно с самого начала было ложным (False), то оператор не будет выполнен ни разу.

Здесь также следует помнить, что позволяется использовать только один оператор после ключевого слова do. Если необходимо выполнить группу операторов, то стоит использовать составной оператор.

Итерационные циклы с постусловием

Операторы между словами repeat и until повторяются, пока логическое выражение является ложным (False). Как только логическое выражение становится истинным (True), происходит выход из цикла.

Так как выражение оценивается после выполнения операторов, то в любом случае операторы выполнятся хотя бы один раз.

Операторы завершения цикла

Для всех операторов цикла выход из цикла осуществляется как вследствие естественного окончания оператора цикла, так и с помощью операторов перехода и выхода.

В версии Турбо Паскаль 7.0 определены стандартные процедуры: Процедура Break выполняет безусловный выход из цикла. Процедура Continue обеспечивает переход к началу новой итерации цикла.

Заметим, что хотя и существует возможность выхода из цикла с помощью оператора безусловного перехода goto, делать этого не желательно. Во всех случаях можно воспользоваться специально предназначенными для этого процедурами Break и Continue.

Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики

Источник