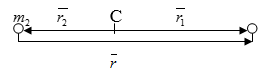Известно что траектории двух материальных точек пересекаются столкнутся
Механическое движение. Система отсчёта
Третий уровень
1.31. Траектории движения двух материальных точек пересекаются. Обязательно ли эти тела сталкиваются? Приведите пример, подтверждающий ваш ответ.
1.32. Самолет взлетает с движущегося в том же направлении авианосца. Одинаковы ли скорости самолета относительно авианосца и Земли?
1.33. Два автомобиля движутся навстречу друг другу (рис. 17). В каком случае скорость первого автомобиля больше: когда его движение рассматривается относительно земли или относительно второго автомобиля?
1.34. Спортсмены пробежали несколько полных кругов по дорожке стадиона. Является ли их траектория замкнутой:
а) относительно Земли;
б) относительно Солнца?
1.35. Начертите траекторию движения, при котором путь превышает модуль перемещения:
б) в 
раз;
1.36. Во время смены караула в Ватикане швейцарский гвардеец прошел по коридору 10 м, повернул направо и прошел 20 м, повернул налево и прошел 10 м, повернул еще раз налево и прошел 50 м, повернул направо и прошел 20 м. Лишь после этого он взял алебарду на караул и замер (рис. 18). Начертите в удобном масштабе траекторию движения гвардейца. Какой путь он прошел? Каков модуль его перемещения?
1.37. Теплоход, двигаясь по Ладожскому озеру, прошел на восток 30 км, затем свернул под углом 45° на северо-восток и прошел еще 20 км, последние 20 км он двигался строго на север. Найдите путь, пройденный теплоходом, и модуль перемещения. Начертите в удобном масштабе траекторию движения.
1.38. Велосипедист движется равномерно по круговой трассе радиусом 1 км, затрачивая на каждый круг 8 мин. Найдите путь и перемещение велосипедиста:
а) за 2 мин; в) за 8 мин;
б) за 4 мин; г) за 12 мин.
1.39. По секундной стрелке больших часов ползет жук. Нарисуйте примерный вид траектории движения жука относительно циферблата, если он дополз от центра часов до конца стрелки за полторы минуты.
1.40. Посмотрите на фотографии (рис. 19) и ответьте:
а) какой путь может пройти конец минутной стрелки за время, прошедшее между двумя снимками;
б) каким может быть модуль перемещения конца минутной стрелки за это время?
1.41. След реактивного самолета (рис. 20) имеет форму окружности (как для стоящего на земле наблюдателя, так и для пилота пассажирского самолета, пролетающего мимо). Значит ли это, что траектория движения реактивного самолета представляет собой окружность и в системе отсчета «пассажирский самолет»?
1.42. Нарисуйте траекторию движения произвольной точки на ободе колеса железнодорожного вагона (рис. 21):
а) относительно вагона;
б) относительно земли.
Известно что траектории двух материальных точек пересекаются столкнутся
1. Система сходящихся сил, действующих на твердое тело, имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.
2. Для равновесия тела под действием системы сходящихся сил необходимо и достаточно, чтобы были равны нулю суммы моментов всех сил данной системы на каждую из координатных осей.
3. Укажите количество независимых уравнений равновесия при действии пространственной системы параллельных сил: 3.
4. Система двух равных по модулю параллельных сил, направленных в противоположные стороны, называется парой сил.
22. Алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки приложения другой силы или, то же самое, равен взятому со знаком плюс или минус произведению модуля одной из сил пары на плечо.
23. Силы, с которыми связи действуют на данное тело, называются реакциями связей.
24. Укажите количество независимых уравнений равновесия при действии на тело произвольной плоской системы сил: 3.
25. Реакция опорной точки перпендикулярна опирающейся поверхности.
26. Теорема о трех силах: Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
27. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен геометрической сумме моментов составляющих пар.
28. Реакция идеальной нити направлена по нити от закрепленного тела.
29. Сумма моментов сил пары относительно произвольной точки равна моменту пары.
30. Для равновесия твердого тела под действием системы сходящихся сил, необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.
31. Задачей статики является изучение методов преобразования систем сил в другие эквивалентные данным.
32. Реакция жесткой заделки состоит из одной силы и пары сил. Момент этой пары называется моментом заделки.
33. Моментом силы относительно оси называется алгебраическая величина, равная проекции вектора момента силы относительно произвольной точки оси на эту ось.
34. Реакция цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, может быть представлена двумя взаимно-перпендикулярными составляющими.
61.Количество независимых уравнений равновесия при действии на ферму произвольной плоской системы сил.
3
62.Центром тяжести твердого тела называется центр параллельных сил тяжести частиц данного тела.
63. Количество независимых уравнений равновесия узла фермы, находящегося под действием плоской системы сходящихся сил:
2
2)Fmaxтр=fN – Закон трения скольжения
70. Центр тяжести треугольника совпадает с точкой пересечения его медиан.
a⃗ =a⃗ r+a⃗ e+a⃗ c, a⃗ c=2ω⃗ e×v⃗ r – Теорема Кориолиса
104. Теорема о сложении скоростей: При сложном движении точки абсолютная скорость равна сумме ее относительной и переносной скоростей.
105. Переносное ускорение точки − это ускорение того места подвижной системы координат, с которым в данный момент совпадает движущаяся точка.
106. Угловая скорость тела при его плоском движении, скорость его произвольной точки A и расстояние от этой точки до мгновенного центра скоростей P связаны соотношением:
ω=vAAP
Да
114. Зависит ли угловая скорость твердого тела, совершающего плоское движение, от выбора полюса?
Не зависти
115. Правило Жуковского: Для определения направления ускорения Кориолиса надо вектор относительной скорости спроецировать на плоскость, перпендикулярную оси вращения в переносном движении, и повернуть в сторону вращения на угол 90 град.
116. Модуль ускорения Кориолиса:
ac=2∣ω⃗ e∣∣v⃗ r∣sinα
Верно
Задача двух тел
Вы будете перенаправлены на Автор24
Приведенная масса
Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.
Рассмотрим замкнутую систему двух материальных точек, взаимодействующих между собой. Как известно центр масс такой системы движется равномерно и прямолинейно (или покоится). Задача просто решается в системе с началом в центре масс, движущейся поступательно (такая система называется Ц-системой).
Непосредственно из рисунка следует соотношение между радиус-векторами:
$\overline
Запишем основные уравнения для движения обеих точек в Ц-системе:
Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.
Готовые работы на аналогичную тему
Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:
Движение двух материальных точек в системе центра масс
В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:
Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:
Задача двух тел решена.
Момент импульса системы двух точек:
\[\overline
\[\overline
задача о движении двух тел сводится к задаче о движении одной точки под действием заданной силы;
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 04 2021
Траектории движения двух материальных точек пересекаются. Означает ли ето что тела сталкиваются?
нет. не означает. через точку пересечения тела могли пройти в разное время
Другие вопросы из категории
электрического взаимодействия между ними после того, как их разместили на расстоянии 4 см друг от друга.
Читайте также
высоты h=2,5м на горизонтальную плиту. Не учитывая силу сопротивления воздуха найти время движения до удара о плиту. 3.Диск радиусом R вращается согласно уравнению зависимости угла поворота от времени w=4+2t+3t3. Определить угловую скорость диска для момента времени t=10с. 4.Скорость материальной точки задана уравнениями vx=8t3+4, vу=6t-3. Определить модуль ускорения точки в произвольный момент времени. 5.Движение материальной точки задано уравнением x=7t^3+4-5t. Определить модуль скорости и ускорения точки в произвольный момент времени. Помогите пожалуйста важен ход решения а не только ответ.
какой момент времени ускорения этих точек одинаковы?
В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v1 и v2 и ускорения а1 и а2 точек в этот момент.
Требуется подробное решение, иначе в курсовую препод не принимает.
скорости и ускорения этой материальной точки и проанализируйте вид движения
вид: х = А+Bt +Ct2, где А = 5,00 м, В = 10,0 м/с, С = 4,00 м/c2. Запишите
уравнение зависимости проекции скорости движения материальной точки на
ось Ох от времени. Определите координату точки и проекцию скорости ее
движения через промежуток времени Δt = 4,00 с от начала движения.
Известно что траектории двух материальных точек пересекаются столкнутся
Тема. Решение задач по теме «Кинематика материальной точки».
Последовательность действий при решении кинематических задач определяется необходимостью записать основные уравнения теории применительно к условиям конкретной задачи. Для этого следует:
Примеры решения расчетных задач
Задача 1. Две машины А и В идут пересекающимися курсами (рис. 1) с заданными скоростями 
и 
. Определите графически наименьшее расстояние, на которое сближаются машины.
Скорости и заданы относительно системы отсчета, связанной с Землей (рис. 1). Задача легко решается, если одна из машин покоится. В этом случае минимальное расстояние будет равно длине перпендикуляра, опущенного из точки, где находится покоящаяся машина, на направление движения другой машины.
Машина будет неподвижна в системе отсчета, связанной с этой машиной. Пусть система отсчета связана с машиной В. Тогда, согласно закону сложения скоростей, скорость машины А в системе отсчета, связанной с машиной В, будет складываться из скорости машины А относительно Земли и скорости 
, с которой Земля движется относительно машины В (рис. 2). Скорость машины А в системе отсчета, связанной с машиной В, находим по правилу сложения векторов. Искомое минимальное расстояние равно ВС.
Ответ: наименьшее расстояние, на которое сближаются машины, равно BC.
Задача 2. Жесткий стержень движется в плоскости так, что скорость точки А стержня равна и направлена под углом α к оси стержня, а скорость точки В направлена под углом β (рис. 3) Найдите скорость точки В.
В системе отсчета, связанной с плоскостью, в которой движется стержень, его движение выглядит очень сложно: оно складывается из поступательного и вращательного движения. Задача сильно упростится, если систему отсчета связать с точкой А. В этой системе отсчета точка В будет двигаться по окружности, а значит скорость этой точки 
будет перпендикулярна стержню (рис. 4). Согласно закону сложения скоростей
, (1)
где 
— скорость, с которой плоскость движения стержня движется относительно точки А, 
.
Векторное равенство (1) целесообразно спроецировать на ось X, направленную вдоль стержня. Тогда получим 
, откуда 
.
Ответ: 
.
Задача 3. Концы стержня А и В скользят по сторонам прямого угла (рис. 5). Как зависит от угла α ускорение середины стержня С, если конец В движется с постоянной скоростью ? Длина стержня l.
Так как 
, то ускорение точки А будет одинаковым в обеих системах отсчета. Спроецируем векторное равенство (2) на ось X. Тогда получим
Ответ: 
.
Задача 4. Скорость монеты , соскальзывающей с клина, стоящего на гладкой горизонтальной поверхности, изображена на рис. 7. Графическим построением найдите скорость клина.
Ответ: шары вернутся к борту, от которого начиналось их движение, одновременно.
Ответ: 
.
Задача 7. Два тела движутся по прямой навстречу друг другу с начальными скоростями v1 и v2 и постоянными ускорениями a1 и a2, направленными противоположно соответствующим скоростям в начальный момент времени. При каком максимальном расстоянии между телами они встретятся в процессе движения?
В системе отсчета, связанной с Землей, встреча двух тел может произойти либо при их движении навстречу друг другу, либо, если одно из тел изменило направление движения раньше, чем произойдет встреча, а другое тело его догонит.
Задачу удобно решать в системе отсчета, связанной с одним из движущихся тел. Тогда в момент встречи скорость второго тела должна обратиться в нуль. Скорость в начальный момент времени и ускорение движущегося тела будут соответственно равны v1 + v2 и a1 + a2. Момент времени, когда произошла встреча, определится из условия, что скорость движущегося тела в этот момент обращается в нуль:
Так как ускорение постоянно, то максимальное расстояние будет равно
Решая совместно (4) и (5), получим
Ответ: 
.
Задача 8. С башни высотой Н под углом α к горизонту (вниз) бросают тело. Одновременно с поверхности Земли под углом α к горизонту бросают второе тело навстречу первому. Определите, на каком расстоянии от подножия башни находится место бросания второго тела, если оба тела столкнулись в воздухе.
Поскольку оба тела движутся в одной плоскости, то движение каждого из них можно представить в виде суммы независимых движений по горизонтали и вертикали. Выберем в качестве тела отсчета Землю. И с телом отсчета свяжем систему координат, имеющую две оси X и Y, начало которой находится у подножия башни (рис. 11).
В момент столкновения координаты этих тел совпадут:
Отсюда получим два уравнения:
которые можно переписать следующим образом:
Поделив первое уравнение на второе, получим 
Ответ:
Задача 9. Мальчик держит один конец доски, а другой ее конец лежит на цилиндре (рис. 12). 
Доска при этом горизонтальна. Затем мальчик двигает доску вперед, вследствие чего цилиндр катится без скольжения по горизонтальной плоскости, отсутствует также скольжение доски по цилиндру. Какой путь должен пройти мальчик, чтобы достичь цилиндра, если длина доски равна L?
Если тело одновременно участвует во вращательном и поступательном движении, то для описания его движения удобно ввести мгновенную ось. Тогда тело в каждый момент времени будет поворачиваться относительно мгновенной оси как целое. Для цилиндра такой мгновенной осью является его образующая О, касающаяся плоскости, по которой он катится (рис. 13). 
Угловая скорость всех точек колеса относительно оси О будет одинаковой. Следовательно, линейная скорость точки, в которой доска соприкасается с цилиндром, будет в 2 раза больше линейной скорости, с которой движется ось цилиндра. Поэтому к тому времени, когда мальчик пройдет расстояние L, ось цилиндра переместится на расстояние L/2. Таким образом, чтобы дойти до цилиндра, мальчик должен пройти расстояние 2L.
Ответ: мальчик должен пройти расстояние 2L.
Задачи для самостоятельной работы
1. Автомобиль и мотоцикл движутся навстречу друг другу со скоростями соответственно равными 12 м/с и 24 м/с. Расстояние между ними в начальный момент времени равно 500 м. Считая, что автомобиль и мотоцикл движутся вдоль оси Х, направленной в сторону движения автомобиля, запишите закон движения х(t) для автомобиля и мотоцикла. В начальный момент времени положение автомобиля совпадает с началом отсчета, и он движется в положительном направлении оси Х.
Ответ: встреча произошла в 10 ч. 30 мин. на середине пути.
3. Пассажир поезда, идущего со скоростью 40 км/ч, видит в течение 3 с встречный поезд длиной 75 м. С какой скоростью идет встречный поезд?
5. Тело бросают вертикально вверх. Промежуток времени между двумя моментами, когда тело проходит точку, находящуюся на высоте Н, равен 
. Найдите начальную скорость 
и время движения.
Ответ: 
7. Камень бросают горизонтально с вершины горы, имеющей угол наклона, равный α. С какой скоростью v должен быть брошен камень, чтобы он упал на расстоянии l (вдоль наклонной плоскости) от вершины? Сопротивлением воздуха можно пренебречь.
Ответ: 
8. Радиус рукоятки колодезного ворота в три раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки при поднятии ведра с глубины 10 метров за 20 секунд?
9. Мальчик вращает камень, привязанный к веревке длиной l=0.55м в вертикальной плоскости, делая число оборотов n=3об/с. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх?
Ответ: 
10. Колесо радиусом 50 см равномерно катится со скоростью 18 км/ч. Какова величина скорости v верхней точки колеса?
11. Обруч бросают на шероховатую горизонтальную плоскость с линейной скоростью v. Одновременно ему сообщают вращательное движение в таком направлении, что он должен катиться по плоскости в ту же сторону (рис. 14). При какой угловой скорости ω обруч покатится по плоскости без скольжения, если радиус обруча R?
Ответ: 