Как решать уравнения с параметром 7 класс
Решение линейных уравнений с параметром аналитическим и графическим способами (7-й класс)
Разделы: Математика
Класс: 7
Цель урока: научиться решать уравнения с параметром линейного вида.
Выполненные на отдельных листах упражнения из домашнего задания, вывешиваются перед уроком на специальной доске для самопроверки.
На конференции 85% делегатов знают английский язык и 75 % испанский. Какая часть делегатов знают оба языка?
в) 3х + 1 = 3х + 1. (х принадлежит R)
с параметром а будем понимать систему значений х и а из области определения уравнения, обращающую его в верное числовое равенство)
а) 
б) 
в) 
Сегодня мы посвятим урок решению задач с параметром аналитическим и графическим способами.
№1. Решите уравнение:
Если а не равно 0, преобразуем уравнение: а+х = а 2 + ах,
а = 1, тогда
Для удобства записи ответа сделаем рисунок решений
Ответ: если а = 0, то решений нет, если а = 1, то х– любое число, если а? 0, а? 1, то х=- а.
Дадим геометрическую интерпретацию уравнения

Назовите пары решения уравнения
Например: а = 1, х = 2,
№ 2 Отцу 40 лет. Через сколько лет отец будет в два раза старше сына?
Пусть сыну а лет. Пусть через х лет отец будет в два раза старше сына.
х + 40 (лет) будет отцу, а + х (лет) будет сыну. Т.к. по условию задачи отец будет в два раза старше сына, то 40 + х = 2 (а + х),
2 способ. Графический
Построим в одной системе координат графики функций у = | х + 2| и у = а.
№ 4 Самостоятельно с последующей проверкой на доске.
При каком значении а уравнение имеет один корень?
Ответ: при любом а корней нет, т.к. сумма двух неотрицательных чисел есть число неотрицательное.
Ответ: при а = 0, единственный корень х = 0.
Это уравнение решить аналитически трудно. Попробуем решить его графически.
Ответ: при а = 1 уравнение имеет единственный корень х = 0.
№ 749 (4) Повторение действий с многочленами. № 737 Текстовая задача.
Необязательное задание: найти натуральное число А, если известно, что из трех данных утверждений два верно, а одно – нет. 1) А + 7 – точный квадрат,
Решение уравнений с параметрами 7 класс
в данной публикации содержатся примеры решения линейных уравнений с параметрами для учащихся 7 класса.
Просмотр содержимого документа
«Решение уравнений с параметрами 7 класс»Примеры решения линейных уравнений, содержащие параметры.
Линейные уравнения с одним неизвестным могут содержать и другие буквы. Такие уравнения называют уравнениями с параметрами. Уравнения, содержащие параметры, решаются также, как и обычные линейные уравнения, но корни уравнения зависят от значений параметров и выражаются через них.
Пример 1. Решим уравнение относительно переменной x:
Перенесем члены уравнения, содержащие x, в левую часть, а все остальные – в правую часть уравнения:
Вынесем x в левой части за скобки:
При p = 5 получаем 0 x = 22, т.е. уравнение корней не имеет.
Если же p ≠ 5, то разделим обе части уравнения на 5 – p.
x =
– уравнение имеет единственный корень.
Ответ: при р ≠ 5 x =
; при р = 5 корней нет.
Мы нашли зависимость решения уравнения от параметра. Если решаем уравнения, содержащие параметры, мы можем сказать, при каких значениях параметра уравнение имеет единственное решение, когда решений бесконечное множество, а в каких случаях их нет вообще.
Пример 2. Решим уравнение относительно переменной x:
x =
Это выражение имеет смысл при любых значениях c и b поэтому уравнение имеет единственное решение.
Ответ: x =
Пример 3. Решим уравнение относительно переменной y:
Если b = 3 и 2 – 2a ≠ 0 (a ≠ 1), то корней нет, т.к. получим равенство, которое не выполняется ни при каких значениях переменной.
Если b = 3 и a = 1, то получим 0 y = 0. Уравнение имеет бесконечное множество решений.
Если b ≠ 3, то y =
– единственный корень.
Ответ: при b ≠ 3 y =
; при b = 3 и a = 1 – бесконечно много решений; при b = 3 и a ≠ 1 – корней нет.
Линейные уравнения с параметрами в 7-м классе (методические рекомендации)
Разделы: Математика
а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если а=10; а=-2;а=0.
Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра аКак было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
Решение.1) (а2-1)=0, а=±1.
При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.
Задачи для самостоятельного решения.
Для всех значений параметров а и в решите уравнения:
Используемая литература.
Урок по алгебре в 7,8 классе «Линейное уравнение с параметром и его решение в общем виде»
Новые аудиокурсы повышения квалификации для педагогов
Слушайте учебный материал в удобное для Вас время в любом месте
откроется в новом окне
Выдаем Удостоверение установленного образца:
Тема: Линейное уравнение с параметром и его решение в общем виде.
Образовательные: дать определение линейного уравнения с параметром, рассмотреть способы его решения, схему исследования линейных уравнений с параметрами. Формировать навыки решения линейных уравнений с параметрами.
Развивающие: развивать уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.
Воспитательные: формирование волевые качества, формирование коммуникабельность, выработка объективной оценки своих достижений, формирование ответственности.
Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.
ученики записывают на доске решения уравнений;
обсуждение, замечания, уточнения к решениям на доске.
Если m = 0, то уравнение примет вид 0 • m = 6 и не имеет решений;
Если m ≠ 0, то уравнение примет вид х =
и имеет единственное решение.
Ответ: при m = 0 нет решений; при m ≠ 0 х =
.
№ 2. При каком значении b уравнение |х| + b = 0 не будет иметь корней?
Если b = 0, то уравнение примет вид |х| = 0, т.е. х = 0 и имеет ед. решение;
Если b > 0, то уравнение не имеет решений;
1. Определение линейного уравнения с параметром.
Уравнение вида Ах = В, (1)
называется линейным уравнением с параметрами.
2. что значит решить уравнение с параметрами?
в) способы решения линейного уравнения.
Линейные уравнения с параметром решаются двумя способами: аналитическим и графическим.
Графический способ решения линейного уравнений с параметром удобен тогда, когда нужно определить количество корней уравнения.
Аналитический способ решения линейного уравнения с параметром удобен тогда, когда требуется найти решение уравнения при каждом значении параметра.
г) схема исследования линейного уравнения (1).
Замечание. Если линейное уравнение не представлено в виде (1), то сначала нужно привести его к виду (1) и только после этого проводить исследование.
№ 1. Решить уравнение: а) (а + 3)х =5.
Ответ: при а = 6 нет решений; при а ≠ 6 х =
.
№ 2. Решить уравнение: а) (а + 4)х = 2а +1.
№ 3. Решить уравнение: а) (а + 1)х = а + 1.
Если а – 4 = 0, т.е. а = 4, то уравнение примет вид 0 • х = 0 и имеет бесконечное
№ 4. Решить уравнение: а) (а – 7)х = а(а – 7).
Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное
№ 5. Решить уравнение (а – 7)х = а 2 – 14а + 49.
Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное
Что нового сегодня Вы узнали на уроке? Дайте определение линейного уравнения с параметрами. Что значит решить уравнение с параметром? Назовите способы решения и схему исследования линейного уравнения с параметром.
Решить уравнения: а) (а – 9)х = 4; б) (а – 6)х = а + 8; в) (а + 3)х = а + 3;
г) (а + 2)х = (а + 2)(а – 3); г) (а + 3)х = а 2 + 6а + 9.
Класс: 7
Презентация к уроку
Тип урока: введение нового материала.
Учебник: «Алгебра-7» авт. Ю.Н.Макарычев, Н.Г. Миндюк и др. издательство «Мнемозина», 2008 год.
I. Проверка домашнего задания (работа выполнялась на двойных листах и сдаётся на проверку).
Готовые решения проецируются на доску и разбирается (проговаривается) алгоритм решения.
№ 624. Решите уравнение:
а) 0,3(2x – 1) – 0,4 (x + 8) = 1,2x – 1;
0,6x – 0,3 – 0,4x – 3,2 = 1,2x – 1;
0,6x – 0,4x –1,2x = 0,3 + 3,2– 1;
– x = 2,5;
x = –2,5. Ответ: – 2,5.в) – 6(2 – 0,2x) + 11 = – 4(3 – 0,3x) – 1;
– 12 + 1,2x + 11 = – 12 + 1,2x – 1;
1,2x – 1,2x = 12 – 11 + 1;
0x = 2. Ответ: решений нет.№ 625. Решите уравнение
а) (2x – 1)(3x + 7) – (1 + 6x)(x + 2) = 4;
6x 2 + 14x – 3x – 7 – (x + 2 + 6×2 + 12x) = 4;
6x 2 + 14x – 3x – 7 – x – 2 – 6×2 – 12x = 4;
6x 2 + 14x – 3x – x – 6x 2 – 12x = 4 + 7 + 2;
– 2x = 13;
x = – 6,5. Ответ: – 6,5.№ 626. Решите уравнение
№ 622. При каких значениях a уравнение ax = 2a – 1:
а) имеет единственный корень; (при a
0)
б) имеет бесконечно много корней; (таких значений a нет)
в) не имеет корней? (при a = 0).II. Устная работа (задания проецируются на доску)
1. Найдите корни уравнения:
а) 14 + 3x = 5 – x ; (– 2,25)
б) 105y – 28 = 105y + 7;
в) 34x + 2 = 34x + 2. (x – любое число)2. При каких значениях a число 3 является корнем уравнения?
3. Укажите контрольные значения, при которых уравнение не имеет решений или решением является любое число?
а) (5 – a) x = 0; б) (b + 4) x = 5; в) ax = x.
III. Изучение нового материала
Учитель. Сегодня на уроке мы с вами будем учиться решать линейные уравнения с параметрами.
Задание 1
Рассмотрим уравнение mx + 3 = 4m – 2x. Оно содержит две переменные: m и x.
1. Вопрос. Чем же они отличаются? (одна из переменных, например m, принимает любые значения, тогда переменная x принимает не все значения, а только те, которые получаются при заданных значениях переменной m).
2. Задание. Решите данное уравнение при m = 2, – 1, 0.
если m = 2, то уравнение примет вид 2x + 3 = 8 – 2x. Ответ:
;
если m = – 1, то уравнение примет вид – x + 3 = – 4 – 2x. Ответ: – 7;
если m = 0, то уравнение примет вид 3 = – 2x. Ответ: – 1,5 )3. Задание. Решите данное уравнение, задав свое значение для переменной m.
Переменную m, значения которой мы задаём, называют параметром (фиксированным числом).
Определение: решить уравнение с параметром – значит, для любых допустимых значений параметра найти значения неизвестной переменной.4. Вопрос. Можем ли мы перебрать все значения параметра m, чтобы найти значения x? (нет)
5. Возникла проблемная ситуация. Как же решить данное уравнение mx + 3 = 4m – 2x?
Нет ли другого подхода к решению уравнения?
Оказывается существует. Для решения линейного уравнения с параметром применяется тот же
алгоритм решения, как и для линейного уравнения без параметра, т.е.перенос слагаемых и
приведение подобных слагаемых. Всегда ли эти операции выполняются? (да).
Выполним указанные операции:6. Вопрос. Всегда ли можно выполнить деление? (нет).
7. Задание. Найдите контрольные значения, при которых уравнение не имеет решений.
Запишем решение уравнения далее так:
Задание 2 (разобрать так же подробно на доске)
Решите уравнение n 2 x + 3nx = 5n + 15;
n 2 x + 3nx = 5n + 15;
n (n + 3) x = 5 (n + 3);
n = – 3; 0 – контрольные значения параметра1) при n = – 3 уравнение примет вид 0x = 0, x – любое число;
2) при n = 0 уравнение примет вид 0x = 15, решений нет;
Задание 3.
Самостоятельное решение уравнений с последующей проверкой на доске.
1. 2кx – 5(2 + x) = 7.
2кx – 5(2 + x) = 7;
2кx – 5x – 10 = 7;
2кx –5x = 7 + 10;
(2к –5) x = 17;
2к –5 = 0, к = 2,5 – контрольное значение параметра1) при к = 2,5 уравнение примет вид 0x = 17, решений нет;
2. a 2 x – 2a = a 2 + ax
a 2 x – 2a = a 2 + ax;
a 2 x – ax = a 2 + 2a;
a(a – 1)x = a (a + 2);
a(a – 1) = 0, a = 0; 1 – контрольные значения параметра1) при a = 0 уравнение примет вид 0x = 0, x – любое число;
2) при a = 1 уравнение примет вид 0x = 3, решений нет;

IV. Подведение итогов
1. Что мы сегодня рассматривали на уроке? (решение линейных уравнений с параметрами.)
2. В чем заключался алгоритм решения таких уравнений? Какие равносильные преобразования применяли?а) освобождение от знаменателя, умножив обе части равенства на одно и тоже отличное от нуля число;
б) раскрытие скобок;
в) перенос слагаемых из одной части равенства в другую с противоположным знаком;
г) приведение подобных слагаемых.V. Выставление оценок
VI. Домашнее задание
1) № 631; № 632; № 633.
2) Дополнительное задание










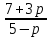 – уравнение имеет единственный корень.
– уравнение имеет единственный корень.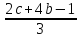
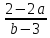 – единственный корень.
– единственный корень.
 и имеет единственное решение.
и имеет единственное решение. .
.
 0)
0) 
 ;
; 




