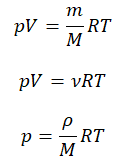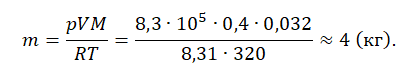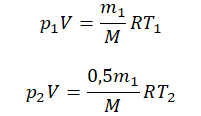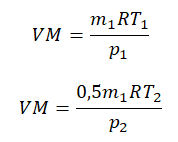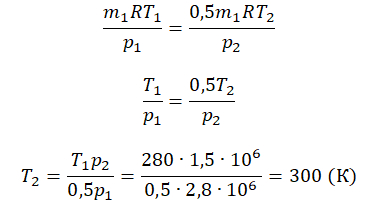Какие макроскопические параметры связывает уравнение клапейрона менделеева
Физика. 10 класс
§ 5. Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Если при переходе идеального газа из одного состояния в другое число его молекул остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений и следует:
где — постоянная Больцмана; — параметры начального состояния газа, а — конечного. Из соотношений (5.1) следует, что
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799–1864), поэтому его называют уравнением Клапейрона.
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
1) не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
2) не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
На рисунке 19 представлен график процесса перехода идеального газа данной массы из состояния 1 в состояние 2. Как изменился объём газа в результате этого процесса?
С учётом выражения (5.4) уравнение (5.3) примет вид:
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834–1907) в 1874 г., поэтому его называют уравнением Клапейрона–Менделеева.
Отметим, что уравнение Клапейрона–Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона–Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Физика. 10 класс
Конспект урока
Урок 20. Уравнение состояния идеального газа. Газовые законы
Перечень вопросов, рассматриваемых на уроке:
2) закон Дальтона, парциальное давление, закон Авогадро;
3) газовые законы и границы их применимости;
4) графики изохорного, изобарного и изотермического процесса;
5) определение по графикам характера процессов и макропараметров идеального газа;
6) применение модели идеального газа для описания поведения реальных газов.
Уравнение, связывающее три макроскопических параметра давление, объём и температура, называют уравнением состояния идеального газа.
Парциальное давление – давление отдельно взятого компонента газовой смеси, равно давлению, которое он будет оказывать, если занимает весь объем при той же температуре.
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами (изопроцессами).
Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.
Процесс изменения состояния термодинамической системы макроскопических тел при постоянном давлении называют изобарным.
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 209 – 218.
Открытые электронные ресурсы по теме урока:
Теоретический материал для самостоятельного изучения
Уравнение Клапейрона при m = const: отношение произведения давления и объёма к температуре есть величина постоянная для постоянной массы газа:
Если изменяется какой-либо макроскопический параметр газа постоянной массы, то два других параметра изменятся таким образом, чтобы указанное соотношение осталось постоянным.
Отношение произведения давления и объёма к температуре равно универсальной газовой постоянной для одного моля идеального газа.
Уравнение Менделеева при v = 1 моль
Произведение постоянной Больцмана и постоянной Авогадро называется универсальной газовой постоянной.

Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона».
Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.
где pi– парциальное давление i-й компоненты смеси.
Парциальное давление – давление отдельно взятого компонента газовой смеси, равное давлению, которое он будет оказывать, если занимает весь объём при той же температуре.
Один моль любого газа при нормальных условиях занимает один и тот же объём равный:
V0=0,0224м 3 /моль=22,4дм 3 /моль.
Это утверждение называется законом Авогадро
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами (изопроцессами).
Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.
Изотерма соответствующая более высокой температуре T1, лежит на графике выше изотермы, соответствующей более низкой температуре T2.
Если значения давления и температуры в различных точках объёма разные, то в этом случае газ находится в неравновесном состоянии.
Процесс изменения состояния термодинамической системы макроскопических тел при постоянном давлении называют изобарным.
Для газа данной массы отношение объема к температуре постоянно, если давление не изменяется — закон Гей-Люссака.
Изобара соответствующая более высокому давлению p2 лежит на графике ниже изобары соответствующей более низкому давлению p1.
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.
Изохора соответствующая большему объему V2 лежит ниже изохоры, соответствующей меньшему объему V1.
Примеры и разбор решения заданий
1. Установите соответствие между физическими величинами и приборами для их измерения. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Какие макроскопические параметры связывает уравнение клапейрона менделеева
где NА — число Авогадро, k — постоянная Больцмана.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
V= const => p/T = const — закон Шарля
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/NA. Отсюда:
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | 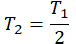 |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | 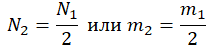 |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | 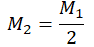 |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
Преобразим уравнения и получим:
Приравняем правые части и выразим искомую величину:

Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Урок-открытие с элементами исследования. Уравнение состояния идеального газа.
Разделы: Физика
Урок проводится в 10 классе, после изучения темы основное уравнение МКТ. (рассчитан на профильный уровень, слайд 0)
Цели урока:
Тип урока: изучение нового материала, с использованием элементов беседы.
Эпиграф к уроку:
«Посев научный взойдет для жатвы народной!»
(Дмитрий Иванович Менделеев) (слайд 1)
Демонстрации: зависимость между объемом, давлением и температурой.
Оборудование: мульдимедийный проектор, компьютер, экран, презентация PowerPoint.
Ход урока
I. Проверка домашнего задания. Повторение ранее изученного. (фронтальный опрос)
Учитель. Здравствуйте ребята. Добрый день. Выполним с вами экспериментальную задачу. Определим атмосферное давление в нашем кабинете. Оборудование: термометр, линейка (рассуждения учащихся).
Ученик. Термометром можно измерить температуру, линейкой измерить размеры комнаты и вычислить объем. А как установить зависимость между давлением, объемом и температурой?
Учитель. И это будет целью нашего урока, вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; научиться использовать закон при решении задач.
Учитель. Что такое идеальный газ? (слайд 2)
Ученик. Идеальным газом называется модель реального газа. Молекулярно-кинетическая теория рассматривает идеальный газ как множество частиц (молекул), расстояние между которыми намного превышает размеры самих частиц, находящихся в состоянии непрерывного хаотичного движения.
Учитель. Назовите условия, при которых газ можно считать идеальным?
Ученик. Газ, удовлетворяющий следующим условиям:
Учитель. Что называется концентрацией?
Ученик. Концентрация – это число молекул в единице объема.
Учитель. Запишите и объясните физический смысл основного уравнения молекулярно-кинетической теории.
II. Постановка проблемного вопроса и решение его
Учитель. Какие параметры, характеризующие газ и процессы, проходящие в нем, называются микроскопическими параметрами (микропараметрами).
Ученик. Состояние идеального газа и процессы, проходящие в нем, будут определяться количеством частиц (молекул), из которых состоит газ, и их параметрами, такими как масса, диаметр, скорость, энергия и пр. (слайд 4) Такие параметры называются микроскопическими или микропараметрами.
Учитель. Какие параметры, характеризующие газ, и процессы, проходящие в нем, называются макроскопическими параметрами (макропараметрами)? (слайд 5)
Ученик. Параметры, характеризующие свойства газа как целого называются макроскопическими или макропараметрами.
Учитель. Если состояние газа не меняется, то не меняются и эти параметры. Назовите макропараметры, характеризующие газ?
Ученик. p – давление, V – объем, T – температура.
Учитель. Температуру, объем, давление и некоторые другие параметры принято называть параметрами состояния газа. Выведем уравнение, устанавливающее зависимость между этими параметрами. (слайд 6)
III. Изучение нового материала
1. Постоянная Лошмидта. Из основного уравнения МКТ идеального газа можно получить уравнение состояния идеального газа, связывающее между собой параметры состояния p, V и Т.
p=nkT (1)
Это соотношение позволяет по двум известным макроскопическим параметрам (давлению и температуре газа) оценить микроскопический параметр (концентрацию).
Найдем концентрацию молекул любого идеального газа при нормальных условиях (н.у.):
Это значение концентрации молекул идеального газа при нормальных условиях называется постоянной Лошмидта.
2. Уравнение Клапейрона.
Получим теперь с помощью равенства (1) новое уравнение. Если известно полное число частиц газа N, занимающего объем V, то число частиц в единице объема
С учетом этого выражение (1) приводится к виду
Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.
Выведенное нами уравнение связывает давление, объем и температуру, которые определяют состояние идеального газа, называется уравнением состояния идеального газа. – уравнение Клапейрона (слайд 7)
Историческая справка. (сообщение ученика, Приложение 1) В 1834 г. Французский физик Б. Клапейрон, работавший длительное время в России (Петербурге), вывел уравнение состояние идеального газа при постоянной массе газа (m=const).(слайд 8)
3. Уравнение Менделеева – Клапейрона.
Рассмотрим случай для произвольной массы газа
R=kNA = 8,31Дж/( моль·К) — универсальная газовая постоянная.
pV=m/M R T — уравнение Менделеева – Клапейрона- уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем и температуру) газа данной массы. (слайд 9)
Историческая справка. (сообщение ученика, Приложение 2) Обобщив уравнение Клапейрона и введя понятие универсальной газовой постоянной, русский ученый Д. И. Менделеев в 1874 г.вывел общее уравнение для состояния идеального газа. (уравнение Менделеева – Клапейрона) (слайд 10)
С помощью данного уравнения можно описывать процессы сжатия и расширения, нагревания и охлаждения идеального газа.
IV.Закрепление изученного материала
1. Беседа с учащимися по вопросам. (слайд 11)
Учитель. Каковы нормальные условия для идеального газа?
Ученик. Нормальные условия для идеального газа: атмосферное давление p=1,013·10 5 Па, температура t=0°С, или Т=273,15К:
Учитель: Какова концентрация молекул идеального газа при нормальных условиях?
Учитель: Какие величины характеризуют состояние газа?
Ученик: Макропараметры p, V, T.
Ученик: Уравнение состояния идеального газа для постоянной массы газа. Уравнение Менделеева – Клапейрона для переменной массы газа
Учитель. Чему равна универсальная газовая постоянная в СИ?
Ученик. R=NAk= 8,31Дж/ моль·К – универсальная газовая постоянная
2. Решение задач у доски с помощью учителя. (слайд 12)
Дополнительная задача. Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.
Вычислите отношение произведения давления на объем к данной температуре, если газ находиться при нормальных условиях
R=8,31 Дж/(моль·К) –универсальная газовая постоянная.
V. Итоги урока
Ученик. Поставленной цели мы достигли: вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; и использовали его при решении задач.
А завершить урок хотелось словами Д.И. Менделеева, обращенными к нам, его потомкам: «Посев научный взойдет для жатвы народной!». И этот год юбилейный, 175-лет со дня рождения великого русского ученого-естествоиспытателя Д.И. Менделеева (слайд 14).
VI. Домашнее задание
§ 53, задачи 2, 5 к § 53.
Презентация — Приложение 4, сообщение ученика о Клапейроне — Приложение 1, сообщение ученика о Менделееве — Приложение 2, задачи для закрепления пройденной темы — Приложение 3.