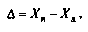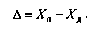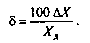какие виды функций преобразования различают в метрологии

Пределение функций преобразования средств измерений по экспериментальным данным

Страницы работы

Фрагмент текста работы

6.7. Определение функций преобразования

средств измерений по экспериментальным данным

6.7.1. Исходные данные

Определение статических характеристик преобразования средств измерений обычно выполняется при их калибровке в метрологических подразделениях с помощью образцовых средств, характеристики погрешности которых и методы выполняемых при этом измерений должны обеспечивать точность результатов измерений, превышающую ожидаемую (декларированную) точность испытуемого средства измерений не менее, чем в 3 ¸ 5 раз.

Пусть статическая характеристика преобразования y=f(x) аппроксимируется степенным полиномом степени p с неизвестными коэффициентами:

. (35)

, i = 1,2. k. (36)

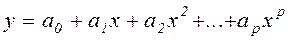
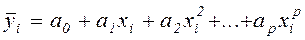
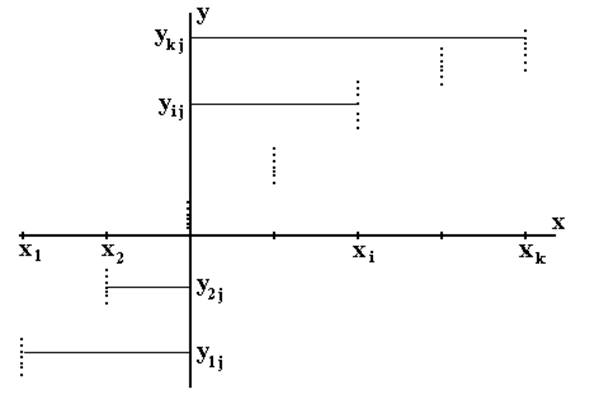
Рис. 15. Графическое представление результатов экспериментов по определению статической характеристики преобразования

6.7.2. Определение функции преобразования

, . (37)

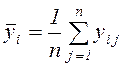
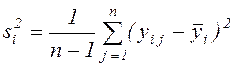
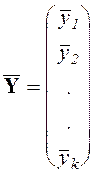
Результаты выполненной предварительной обработки исходных данных записывают в виде вектора средних значений и матрицы оценок дисперсий:

, . (38)

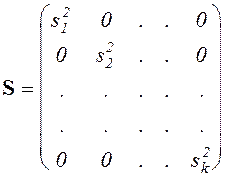
Равенства (36) образуют систему уравнений, которая может быть записана в матричном виде

, (39)

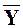
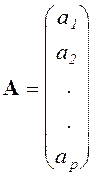
где вектор определен в (38). Матрица X и вектор A имеют вид

, . (40)

Всегда желательно, чтобы k > p + 1. Таким образом создается полезная избыточность, повышающая устойчивость оценок коэффициентов полинома. Но при этом матрица X неквадратная, и система (39) не имеет решения в обычном смысле. Для получения решения эту систему преобразуют к системе с квадратной матрицей путем умножения слева на транспонированную матрицу :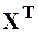

,

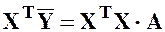
Решая эту систему, получают вектор оценок коэффициентов полинома:

. (41)

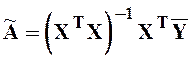
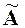
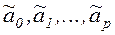
Компонентами вектора являются оценки коэффициентов полинома (35). Описанный метод их получения называется методом наименьших квадратов (МНК), поскольку полином с такими коэффициентами пройдет между экспериментальными точками так, что сумма квадратов расстояний от него до этих точек окажется минимальным.

На практике точность измерений значений выходного сигнала при разных значениях входного сигнала может быть различной. Понятно, что более точным результатам следует придавать больший вес, чем менее точным. С этой целью в уравнение (41) вводится матрица S :

. (42)

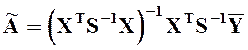
Дисперсии этих оценок суть диагональные элементы матрицы

. (43)

6.7.3. Определение коэффициента преобразования

При разработке и изготовлении средств измерений обычно стремятся к тому, чтобы их функции преобразования были линейными по отношению к информативному параметру измеряемого или преобразуемого сигнала измеряемой величины. Мало того, обычно добиваются, чтобы эти функции обязательно проходили через начало координат.

Незначительная нелинейность и ненулевое значение выходного сигнала при нуле входного учитываются в составе систематической составляющей погрешности средства измерений. Значение этой погрешности зависит от входной величины и является

Источник

Измерительные преобразования физических величин

Измерительные преобразования физических величин

Измерительное преобразование – однозначное преобразование одной физической величины в другую физическую величину или сигнал, функционально с ней связанные, удобные для обработки, хранения и дальнейшего преобразования. Любое измерение, по существу, сводится к совокупности отдельных измерительных преобразований.

Измерительный преобразователь – техническое устройство, построенное на определённом физическом явлении и выполняющее одно частое преобразование.

Понятие “измерительное преобразование” существенно шире, чем “измерительный преобразователь”, поскольку одно измерительное преобразование можно осуществить множеством различных преобразователей.

Пример. Преобразование изменения температуры Т в перемещение Δх:

Классификация измерительных преобразователей

По виду ФВ на входе ИП и ФВ на выходе:

По виду зависимости ФВ величин от времени на входе и на выходе:

По наличию или отсутствию энергии в измеряемом сигнале:

По виду модуляции сигнала на выходе ИП:

По виду динамических процессов, протекающих в ИП в процессе преобразования:

Примеры статических преобразователей.

Акселерометр – прибор, измеряющий ускорение объекта. В данном случае постоянное ускорение преобразуется в постоянный угол отклонения маятника от положения равновесия.

Аналогичное преобразование имеет место в пружинных весах, где постоянная сила тяжести преобразуется в постоянное смещение пружины.

В пьезоэлектрических весах вес груза преобразуется в деформацию пьезокристалла, в котором возникает разность потенциалов, измеряемая вольтметром.

Примеры динамических преобразователей

Гравиметры измеряют статическую величину – ускорение свободного падения g. В обоих примерах эта статическая величина преобразуется в сигнал, выражаемый через динамические параметры гравиметра (период колебаний в первом случае и время движения вверх-вниз тела, брошенного вверх, – во втором). В обоих случаях процессе преобразования сопровождается превращением потенциальной энергии в кинетическую и наоборот.

В модуляционном преобразователе Ф – постоянный световой поток электрической лампочки (статический сигнал) превращается в периодический сигнал – переменный ток I.

Статические характеристики и статические погрешности СИ

Основная статическая характеристика СИ – функция преобразования. Функция преобразования – функциональная зависимость выходной величины от входной. Эта зависимость может описываться аналитически, графически или в виде таблицы. В случае аналитического описания будем писатьy=F(x).

Вводят также понятие чувствительности СИ, как производной y по x: . В общем (нелинейном) случае S зависит от x. В СИ стремятся иметь линейную функцию преобразования. Как будет показано в дальнейшем, это позволяет уменьшить погрешность, связанную с наличием шумов. В этом случае , и тогда вводят обозначение . Коэффициент K называют коэффициентом преобразования или масштабным коэффициентом. Очевидно, что K равен тангенсу угла наклона прямой y(x) к оси x (см. рис.).

Различают три вида функции преобразования:

Номинальная – указывается в документации на CИ.

Индивидуальная – устанавливается путём экспериментальных исследований данного экземпляра СИ при определённых значениях влияющих величин.

Действительная (реальная) – реализуется в данных условиях, в данное время, в данном месте.

Источник

Основные понятия, связанные со средствами измерений

Средством измерения (СИ) называется техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и хранящее единицу физической величины, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Средства измерения классифицируют по следующим признакам:

по конструктивному исполнению;

По конструктивному исполнению СИ подразделяются на: меры, измерительные приборы, измерительные преобразователи, измерительные установки, измерительные системы.

Мера — это средство измерения, предназначенное для воспроизведения физической величины заданного размера. Например: гиря — мера массы, резистор — мера электрического сопротивления.

Измерительный преобразователь — это средство измерения, предназначенное для выработки измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки или хранения, но недоступной для непосредственного восприятия наблюдателем (термопара, частотный преобразовател ь).

Измерительные преобразователи могут быть первичными, к которым подведена измеряемая величина, и промежуточными, которые располагаются в измерительной цепи за первичными. Примерами первичных измерительных преобразователей являются термопары, датчики.

Измерительный прибор — средство измерения, предназначенное для получения значений измеряемой физической величины в установленном диапазоне (рН-метры, весы, фото-электроколориметры и т.д.).

Под измерительной установкой понимают совокупность средств измерений (мер, измерительных приборов, преобразователей) и вспомогательных устройств для выработки сигналов информации в форме, удобной для восприятия и расположенных в одном месте (испытательный стенд).

Измерительная система — это совокупность средств измере-ний и вспомогательных устройств, соединенных между собой каналами связи, размещенных в разных точках контролируемого пространства с целью измерения одной или нескольких физических величин, свойственных этому пространству (контролирующие, управляющие системы с ЭВМ).

По метрологическому назначению СИ подразделяются на рабочие и метрологические. Рабочие средства измерения предназначены непосредственно для измерений в различных сферах деятельности, а именно в науке, технике, в производстве, медицине, то есть там, где необходимо получить значение той или иной физической величины. Метрологическое средство измерения предназначено для метрологических целей: воспроизведения единицы и ее хранения или передачи размера единицы рабочим СИ. К ним относятся эталоны, образцовые СИ, поверочные установки, стандартные образцы.

По уровню стандартизации различают стандартизованные и нестандартизованнные средства измерения. Стандартизованными считаются средства измерения, изготовленные в соответствии с требованиями государственного стандарта и соответствующие техническим характеристикам установленного типа средств измерения, полученным на основании государственных испытаний, и внесенные в Государственный реестр СИ. Нестандартизованные — уникальные средства измерения, предназначенные для специальной измерительной задачи, в стандартизации требований к которым нет необходимости. Они не подвергаются государственным испытаниям, а подлежат метрологической аттестации.

Метрологическое средство измерения чаще именуется «эталон».

Чтобы обеспечить единство измерений, необходима тождественность единиц, в которых проградуированы все средства измерений одной и той же физической величины. Для этого применяют средства измерений, хранящие и воспроизводящие установленные единицы физических величин и передающие их соответствующим средствам измерений. Высшим звеном в метрологической передаче размеров единиц являются эталоны.

Эталон единицы — средство измерений (или комплекс средств), обеспечивающее воспроизведение и (или) хранение единицы с целью передачи ее размера нижестоящим по поверочной схеме средствам измерений, выполненное по особой спецификации и официально утвержденное в установленном порядке в качестве эталона.

Эталон, обеспечивающий воспроизведение единицы с наивысшей в стране (по сравнению с другими эталонами той же единицы) точностью, называется первичным.

Специальный эталон воспроизводит единицу в особых условиях и заменяет при этих условия первичный эталон.

Первичный или специальный эталон, официально утвержденный в качестве исходного для страны, называется государственным.

В метрологической практике широко используют вторичные эталоны, значения которых устанавливается по первичным эталонам. Вторичные эталоны являются частью подчиненных средств хранения единиц и передачи их размера. Они создаются и утверждаются в тех случаях, когда это необходимо для обеспечения наименьшего износа государственного эталона.

Вторичные эталоны по своему назначению делятся на эталоны-копии, эталоны сравнения, эталоны-свидетели и рабочие эталоны.

Эталон-копия предназначен для передачи размеров единиц рабочим эталонам. Он не всегда является физической копией государственного эталона.

Эталон-свидетель предназначен для проверки сохранности государственного эталона и для замены его в случае порчи или утраты.

Эталон сравнения применяют для сличения эталонов, которые по тем или иным причинам не могут быть непосредственно сличаемы друге другом (например, так называемый нормальный элемент, используемый для сличения государственного эталона Вольта с эталоном Вольта Международного бюро мер и весов).

Рабочий эталон применяют для передачи размера единицы образцовым средствам измерений высшей точности, а в отдельных случаях — наиболее точным средствам измерений.

Образцовое средство измерения — мера, измерительный прибор или измерительный преобразователь, служащие для поверки по ним других средств измерений и утвержденные в качестве образцовых.

Поверка средств измерений — определение метрологическим органом погрешности средств измерений и установления его пригодности к применению.

Образцовые средства измерений могут иметь разные разряды. Между ними существует соподчиненность: образцовые средства измерений первого разряда поверяют, как правило, непосредственно по рабочим эталонам, образцовые средства измерений второго и последующих разрядов подлежат поверке по образцовым средствам измерений непосредственно предшествующих разрядов. Для разных видов измерений устанавливается, исходя из требований практики, различное число разрядов образцовых средств измерений.

Рабочее средство измерений применяют для измерений, не связанных с передачей размеров единиц.

Средство измерений — техническое средство, имеющее нормированные метрологические характеристики. Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками. Перечень важнейших из них регламентируется ГОСТ «Нормируемые метрологические характеристики средств измерений». Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации, посредством отдельных средств измерений или совокупности средств измерений, например, автоматических измерительных систем.

Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования (иначе называемая функцией преобразования или градуировочной характеристикой). Она устанавливает зависимость y = f(x) информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала. Если статическая характеристика преобразования линейна, т.е. у= Кх, то коэффициент К называется чувствительностью измерительного прибора (преобразователя).

Важной характеристикой шкальных измерительных приборов является цена деления, т.е. то изменение измеряемой величины, которому соответствует перемещение указателя

на одно деление шкалы. Если чувствительность постоянна в каждой точке диапазона измерения, то шкала называется равномерной. При неравномерной шкале нормируется наименьшая цена деления шкалы измерительных приборов. У цифровых приборов шкалы в явном виде нет, и на них вместо цены деления указывается цена единицы младшего разряда числа в показании прибора.

Важнейшей метрологической характеристикой средств измерений является погрешность.

Под абсолютной погрешностью меры понимается алгебраическая разность между ее номинальным Х_н и действительным Х_Д значениями:

а под абсолютной погрешностью измерительного прибора — разность между его показанием Х_П и действительным значением Х_п измеряемой величины:

Однако в большей степени точность средства измерений характеризует относительная погрешность, т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины:

Обычно лямда регистрирующих приборах, как правило, осуществляется печатание показаний с помощью алфавитно-цифровых печатающих устройств со скоростью до 10 3 знаков в секунду. Для долговременного хранения информации используются также различные виды запоминающих устройств.

Цифровое отсчетное или регистрирующее устройство никак не ограничивает точность цифрового прибора, так как цифровой код без какой-либо погрешности может быть изображен на цифровом отсчетном устройстве.

Однако не всегда цифровое отсчетное или регистрирующее устройство лучше аналогового. При большом числе одновременно измеряемых величин (контроль сложного объекта) показания аналоговых приборов воспринимаются легче, так как независимо от цифр на шкале пространственное положение указателя и характер его перемещения или осциллограмма регистрируемого процесса позволяет более оперативно проводить анализ контролируемого процесса.

Для показывающих приборов обычно не требуется высокого быстродействия в силу ограниченности возможностей оператора при приеме информации.

По структурному принципу различают измерительные устройства прямого действия (преобразования), в которых реализуется метод непосредственной оценки; измерительные устройства, работа которых основана на методе сравнения. В измерительных приборах прямого действия преобразование сигнала происходит в одном направлении последовательно. Операция сравнения осуществляется с помощью сравнивающего устройства (СУ), в котором обычно одна величина вычитается из другой. Используя выходной сигнал СУ, с помощью преобразователя можно управлять мерой и реализовать нулевой метод сравнения. В связи с тем что в измерительных устройствах, основанных на методе сравнения, измеряемая

величина уравновешивается (компенсируется) величиной, воспроизводимой мерой, их также называют измерительными устройствами с уравновешивающим (компенсационным) преобразователем. Измерительные устройства в общем случае имеют более высокую точность за счет использования меры. Отмечают также различие требований к отдельным преобразователям измерительных устройств с точки зрения обеспечения измерительных устройств. Так, в ИУ непосредственной оценки общий коэффициент передачи К = К1 К2 и его точность определяются соответствующей точностью всех преобразователей.

По структурным признакам ИУ также можно классифицировать по числу каналов и по временной последовательности преобразований входных сигналов. В зависимости от числа входных сигналов, несущих информацию об измеряемой величине, ИУ бывают с одним (например, вольтметр), двумя (фазометр) и более входами, т.е. соответственно одно-, двух- и многоканальными. В зависимости от временной последовательности преобразований входных сигналов (если их более двух) различают ИУ с одновременным (параллельным) и последовательным преобразованием. При последовательном преобразовании сигналы обрабатываются поочередно, причем за цикл измерения каждый сигнал через входное переключающее устройство (коммутатор) подается на вход преобразователя один раз. Разновидностью последовательного преобразователя является периодическое устройство, когда за время одного цикла измерения сигналы переключаются многократно. Последовательное преобразование позволяет уменьшить аппаратурные затраты за счет перехода от многоканальной структуры к одноканальной с входным коммутатором.

Источник

Мокров Ю. Метрология, стандартизация, сертификация

ОГЛАВЛЕНИЕ

Глава 3. Cредства измерений и их свойства

Измерения выполняются с помощью технических средств, которые называются средствами измерений (СИ). Разработка СИ является задачей приборостроения. В метрологии СИ рассмат-риваются с точки зрения их единой классификации и выявления параметров, которые обеспечивают получение результата измерений с заданной точностью. Здесь же рассматриваются методы и средства передачи размеров единиц от эталонов к рабочим средствам измерений.

Оценка пригодности средств измерений для решения тех или иных измерительных задач проводится путем рассмотрения их метрологических характеристик.
Метрологическая характеристика (МХ) – характеристика одного из свойств средства измерений, влияющая на результат измерений и его погрешность. Метрологические характеристики позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью. Метрологические характеристики, устанавливаемые нормативными документами на средства измерений, называют нормируемыми метрологическими характеристиками, а определяемые экспериментально – действи-тельными.
Для каждого типа СИ устанавливаются свои метрологические характеристики. Ниже рассматриваются наиболее распространенные на практике метрологические характеристики.
Диапазон измерений СИ – область значений величины, в пределах которой нормированы его допускаемые пределы погрешности. Для мер это их номинальное значение, для преобразователей — диапазон преобразования. Различают нижний и верхний пределы измерений, которые выражаются значениями величины, ограничивающими диапазон измерений снизу и сверху.
Погрешность СИ — разность между показанием средства измерений – Хп и истинным (действительным) значением измеряемой величины – Х д.
Существует распространенная классификация погрешностей средств измерений. Ниже приводятся примеры их наиболее часто используемых видов.
Абсолютная погрешность СИ – погрешность средства измерений, выраженная в единицах измеряемой величины: DХ = Хп – Хд. Абсолютная погрешность удобна для практического применения, т.к. дает значение погрешности в единицах измеряемой величины. Но при ее использовании трудно сравнивать по точности приборы с разными диапазонами измерений. Эта проблема снимается при использовании относительных погрешностей.
Если абсолютная погрешность не изменяется во всем диапазоне измерения, то она называется аддитивной, если она изменяется пропорционально измеряемой величине (увеличивается с ее увеличением), то она называется мультипликативной
Относительная погрешность СИ – погрешность средства измерений, выраженная отношением абсолютной погрешности СИ к результату измерений или к действительному значению измеренной величины: d = DХ / Хд. Относительная погрешность дает наилучшее из всех видов погрешностей представление об уровне точности измерений, который может быть достигнут при использовании данного средства измерений. Однако она обычно существенно изменяется вдоль шкалы прибора, например, увеличивается с уменьшением значения измеряемой величины. В связи с этим часто используют приведенную погрешность.
Приведенная погрешность СИ – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины ХN, которое называют нормирующим: g = DХ / ХN..
Относительные и приведенные погрешности обычно выражают либо в процентах, либо в относительных единицах (долях единицы).
Для показывающих приборов нормирующее значение устанавливается в зависимости от особенностей и характера шкалы. Приведенные погрешности позволяют сравнивать по точности средства измерений, имеющие разные пределы измерений, если абсолютные погрешности каждого из них не зависят от значения измеряемой величины.
По условиям проведения измерений погрешности средств измерений подразделяются на основные и дополнительные.
Основная погрешность СИ – погрешность средства измерений, применяемого в нормальных условиях, т.е. в условиях, которые определены в НТД не него как нормальные. Нормальные значения влияющих величин указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями. Наиболее типичными нормальными условиями являются:

— относительная влажность (65±15) %;

Иногда вместо номинальных значений влияющих величин указывается нормальная область их значений. Например, влажность (30 – 80) %.
Дополнительная погрешность СИ – составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения. Деление погрешностей на основные и дополнительные обусловлено тем, что свойства средств измерений зависят от внешних условий.
Погрешности по своему происхождению разделяются на систематические и случайные.
Систематическая погрешность СИ – составляющая погрешности средства измерений, принимаемая за постоянную или закономерно изменяющуюся. Систематические погрешности являются в общем случае функциями измеряемой величины и влияющих величин (температуры, влажности, давления, напряжения питания и т.п.).
Случайная погрешность СИ – составляющая погрешности средства измерений, изменяющаяся случайным образом. Случайные погрешности средств измерений обусловлены случайными изменениями параметров составляющих эти СИ элементов и случайными погрешностями отсчета показаний приборов.
При конструировании прибора его случайную погрешность стараются сделать незначительной в сравнении с другими погрешностями. У хорошо сконструированного и выполненного прибора случайная погрешность незначительна. Однако при увеличении чувствительности средств измерений обычно наблюдается увеличение случайной погрешности. Тогда при повторных измерениях одной и той же величины в одних и тех же условиях результаты будут различными. В таком случае приходится прибегать многократным измерениям и к статистической обработке получаемых результатов. Как правило, случайную погрешность приборов снижается до такого уровня, что проводить многократные измерений нет необходимости.
Стабильность СИ — качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик.
Градуировочная характеристика СИ – зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. Может быть выражена в виде формулы, графика или таблицы.

3.3 Использование СИ

Средства измерений можно использовать только тогда, когда известны их метрологические характеристики. Обычно указываются номинальные значения параметров средств измерений и допускаемые отклонения от них. Сведения о метрологических характеристиках приводятся в технической документации на средства измерений или указываются на них самих. Как правило, реальные метрологические характеристики имеют отклонения от их номинальных значений. Поэтому устанавливают границы для отклонений реальных метрологических характеристик от номинальных значений – нормируют их. Нормирование метрологических характеристик средств измерений позволяет избежать произвольного установления их характеристик разработчиками.
C помощью нормируемых метрологических характеристик решаются следующие основные задачи:

Нормирование характеристик СИ проводится в соответствии с положениями стандартов. Например, ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений». Соответствие средств измерений установленным для них нормам делает эти средства взаимозаменяемыми.
Одной из важнейших метрологических характеристик СИ является их погрешность, знание которой необходимо для оценивания погрешности измерения.
Необходимо отметить, что погрешность СИ является только одной из составляющих погрешности результата измерений, получаемого с использованием данного СИ. Другими составляющими являются погрешность метода измерений и погрешность оператора, проводящего измерения.
Погрешности средств измерений могут быть обусловлены различными причинами:

3.5 Класс точности СИ и его обозначение

Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точности СИ.
Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей (они рассмотрены выше), а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах.
При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответ-ствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.
Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе
В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров.
Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице.

Обозначение классов точности

___________________________________________________________
Пределы допускаемой Обозначения Форма выраже-
основной погрешности ния погрешности
в документации на приборе
g = ± 1,5 Класс точности 1,5 1,5 Приведенная
погрешность

d = ± 0,5 Класс точности 0,5 0,5 Относительная
погрешность,
постоянная

d = ± [ 0,02 + 0,01( xk/x –1)] Класс точности 0,02/0,01 Относительная
0,02/0,01 погрешность,
возрастает с
уменьшением х

Результаты калибровки удостоверяются калибровочным знаком, наносимым на СИ, или сертификатом о калибровке. Калибровке присущ ряд особенностей по сравнению с поверкой. Это добровольная процедура и она может выполняться любой метрологической службой. При этом аккредитация на право калибровки также является добровольной (не обязательной) процедурой.
Отмеченные особенности калибровки являются следствием разгосударствления процессов контроля за метрологической исправностью средств измерений – отказом от их всеобщей обязательности поверки.
Хотя калибровка может проводиться любой метрологической службой и является добровольной процедурой, для ее проведения необходимы определенные условия. Основное из них – прослеживание измерений, т.е. обязательная передача размера единицы от эталона к калибруемому рабочему средству измерений.
Для организации работ по калибровке в РФ создана Российская система калибровки (РСК), в которую входят государственные научные метрологические центры, органы ГМС, метрологические службы юридических лиц, объединенные целью ОЕИ в сферах, не подлежащих государственному метрологическому контролю и надзору.
Российская система калибровки базируется на следующих принципах:

Источник