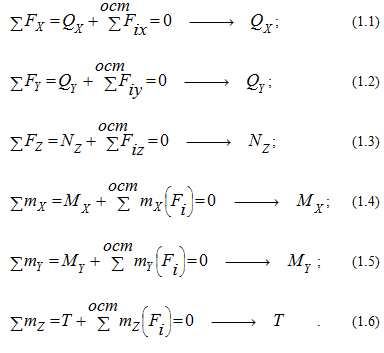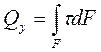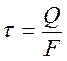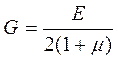какие внутренние силовые факторы возникают при сдвиге и смятии
Внутренние силовые факторы — справочник
Привет! Этот справочник, на портале – SoproMats, будет по внутренним силовым факторам при различных видах деформаций: растяжении и сжатии, кручении и изгибе. По каждому фактору будет написана специальная статья, где расскажем, как обозначается, в чем измеряется и как рассчитывается. Для подробного изучения каждого силового фактора, перемещайтесь по указанным гиперссылкам.
ВСФ при растяжении и сжатии
Как известно, при растяжении и сжатии (центральном) возникает один единственный внутренний силовой фактор – продольная сила. В указанной статье рассказывается, что это за сила, в чем измеряется и т.д.
Если вкратце рассказывать, то продольная сила рассчитывается методом сечений, который предполагает, что если вся конструкций находится в равновесии, то и отдельные ее части также будут находится в равновесии, если действие частей друг на друга заменить силовыми факторами.
ВСФ при кручении
При кручении, также как при растяжении и сжатие, в поперечных сечениях действует один силовой фактор – крутящий момент. В статье рассказывается об данном факторе, как он рассчитывается, в каких расчетах используется и как обозначается.
ВСФ при поперечном изгибе
При поперечном изгибе, чаще всего, в сечениях возникают два силовых фактора – поперечная сила и изгибающий момент. Поперечная сила, как правило, используется в проверочном расчете на прочность по касательным напряжениям, а также служит вспомогательным инструментов для определения экстремумов на эпюре изгибающих моментов.
Изгибающий момент используется при проведения прочностных расчетов по нормальным напряжениям. Подробнее об данных величинах можете узнать, перейдя по указанным ссылочкам.
iSopromat.ru
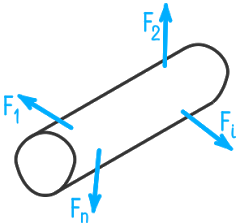
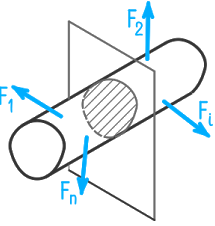
Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.
По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:
надо мысленно рассечь брус, находящийся в равновесии, на две части
и рассмотреть равновесие одной из них.
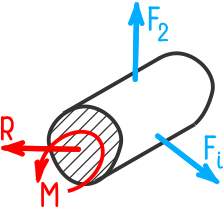
Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.
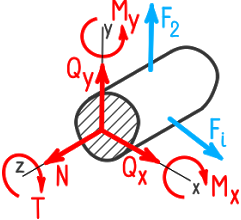
Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Правила знаков для внутренних силовых факторов
Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:
Эпюры внутренних силовых факторов
В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 2.2. Растяжение и сжатие
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
В случаях, когда рабочее напряжения значительно ниже допускаемых σ
Тема 2.3. Практические расчеты на срез и смятие. Основные предпосылку расчетов и расчетные формулы
Иметь представление об основных предпосылках и условностях расчетов о деталях, работающих на срез и смятие.
Знать внутренние силовые факторы, напряжения и деформации при сдвиге и смятии, условия прочности.
Уметь определять площади среза и смятия.
Детали соединений (болты, штифты, шпонки, заклепки) работают так, что можно учитывать только один внутренний силовой фактор — поперечную силу. Такие детали рассчитываются на сдвиг.
Сдвиг (срез)

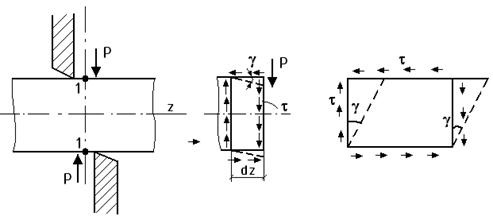
Рассмотрим брус, на который действуют равные по величине, противоположно направленные, перпендикулярные продольной оси силы (рис. 23.1).
Применим метод сечений и определим внутренние силы упругости из условия равновесия каждой из частей бруса:
где Q — поперечная сила. Естественно считать, что она вызовет появление только касательных напряжений τ.
Рассмотрим напряженное состояние в точке В поперечного сечения.
Выделим элемент в виде бесконечно малого параллелепипеда, к граням которого приложены напряжения (рис. 23.2).
Исходя из условия равновесия точки В, внутри бруса при возникновении касательного напряжения τ на правой вертикальной площадке такое же напряжение должно возникнуть и на левой площадке. Они образуют пару сил. На горизонтальных площадках возникнут такие же напряжения, образующие такую же пару обратного направления (рис. 23.3).
Такое напряженное состояние называется чистым сдвигом. Здесь действует закон парности касательных напряжений:
При сдвиге в окрестностях точки на взаимно перпендикулярных площадках возникают равные по величине касательные напряжения, направленные на соседних площадках либо от ребра, либо к ребру (рис. 23.3а).
В результате площадки сдвигаются на угол γ, называемый углом сдвига.
При сдвиге выполняется закон Гука, который в данном случае записывается следующим образом:
Здесь τ — напряжение; G — модуль упругости сдвига; γ — угол сдвига.
При отсутствии специальных испытаний G можно рассчитать по формуле
Е — модуль упругости при растяжении.
Расчет деталей на сдвиг носит условный характер.
Для упрощения расчетов принимается ряд допущений:
— при расчете на сдвиг изгиб деталей не учитывается, хотя силы, действующие на деталь, образуют пару;
— при расчете считаем, что силы упругости распределены по сечению равномерно;
— если для передачи нагрузки используют несколько деталей, считаем, что внешняя сила распределяется между ними равномерно.
 |
Откуда формула для расчета напряжений имеет вид:
где τс — касательное напряжение; Q — поперечная сила; Ас — площадь сдвига; F — внешняя сдвигающая сила; z — количество деталей.
 |
Условие прочности при сдвиге (срезе)
 |
[τс] — допускаемое напряжение сдвига, обычно его определяют по формуле
При разрушении деталь перерезается поперек. Разрушение детали под действием поперечной силы называют срезом.
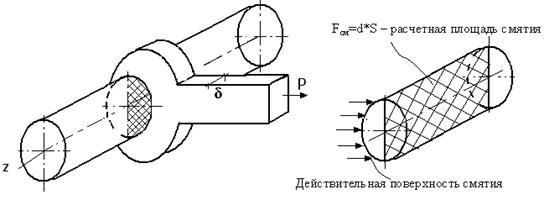
Смятие
Довольно часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта в результате передачи нагрузки от одной поверхности к другой. При этом на поверхности возникают сжимающие напряжения, называемые напряжениями смятия, σсм.

Таким образом, условие прочности при смятии можно выразить соотношением
где d — диаметр окружности сечения; δ — наименьшая высота соединяемых пластин; Асм — расчетная площадь смятия; F — сила взаимодействия между деталями, допускаемое напряжение смятия:
Сдвиг и смятие



Расчеты на прочность и жесткость при кручении.
| Расчеты на прочность | Расчеты на жесткость |
| 1. Проверочный расчет | |
| Условие прочности | Условие жесткости |
 |  |
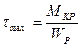 |  |
  %- погрешность %- погрешность | 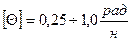 |
| а) определение d вала | |
 |  |
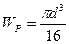 | 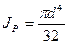 |
 |  |
| б) определение крутящего момента | |
 |  |
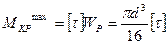 |  |
Смятие – такой вид деформации бруса, при которой в любом его поперечном сечении возникает только поперечная сила.
При изгибе возникают только касательные напряжения, они всегда парные.
Условие прочности при сдвиге:
Плоское напряженное состояние, при котором в окрестности точки можно выделить элементарный параллелепипед, на боковых гранях которого действуют только касательные напряжения, называется чистым сдвигом.
G – модуль сдвига – модуль упругости II рода.
| Упругие константы любого материала: | –  (коэффициент Пуассона; (коэффициент Пуассона; |
| – E(модуль Юнга); | |
 | – G(модуль упругости II рода) |
Сдвиг, приводящий к разрушению материала, называется срезом для пластических материалов и скалыванием для хрупких материалов.

Смятие – деформация, обусловленная местным сжатием материала в соприкасающихся деталях по площадкам передачи давления.
Условие прочности на смятие: