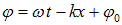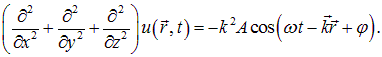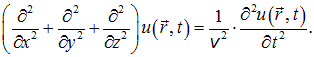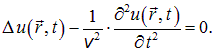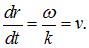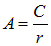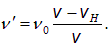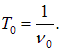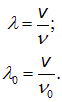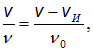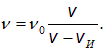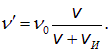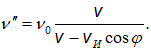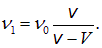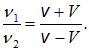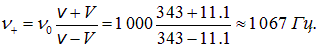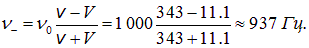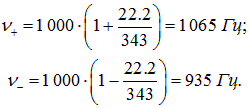какие волны называются сферическими

СФЕРИЧЕСКАЯ ВОЛНА

— волна, радиально расходящаяся от нек-рой точки (источника) или сходящаяся к ней (к стоку) и имеющая сферич. волновые фронты (поверхности равных фаз). Простейшим примером является сферически симметричная скалярная волна вида

Существуют и несимметричные С. в., амплитуды к-рых зависят от полярной q и азимутальной j угл. координат, но фазовые фронты по-прежнему остаются сферическими:

где U(r, t )отвечает симметричной С. в., напр. в форме (1) или (2), a D(q,j) описывает угл. зависимость поля (эту ф-цию можно представить в виде суперпозиции т. н. сферич. гармоник). В однородных изотропных средах волновое поле на больших расстояниях от центра почти всегда имеет вид (3). Подбором D можно концентрировать поле около заданных направлений, поэтому ф-ция D(q, j) наз. диаграммой направленности излучения источника (см. Антенна).

Лит. см. при ст. Волны. М. А. Миллер, Л. А. Островский.

Полезное

Смотреть что такое «СФЕРИЧЕСКАЯ ВОЛНА» в других словарях:

Сферическая волна — 73. Сферическая волна Волна, фронт которой представляет собой сферическую поверхность, радиусы которой совпадают с направлениями распространения волны Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа 2.2.7 сферическая… … Словарь-справочник терминов нормативно-технической документации

сферическая волна — sferinė banga statusas T sritis fizika atitikmenys: angl. spherical wave vok. Kugelwelle, f rus. сферическая волна, f; шаровая волна, f pranc. onde sphérique, f … Fizikos terminų žodynas

Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия

Сферическая радиоволна — 50. Сферическая радиоволна Сферическая волна Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

ВОЛНА — возмущение среды или поля, распространяющееся в этой среде или в этом поле; (1) В. акустическая упругая В., распространяющаяся в твёрдой, жидкой или газообразной среде; (2) В. обратная В., движущаяся в сторону её источника; (3) В. падающая В.,… … Большая политехническая энциклопедия

шаровая волна — sferinė banga statusas T sritis fizika atitikmenys: angl. spherical wave vok. Kugelwelle, f rus. сферическая волна, f; шаровая волна, f pranc. onde sphérique, f … Fizikos terminų žodynas

Волны — Волна изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой… … Википедия

ГОСТ 24375-80: Радиосвязь. Термины и определения — Терминология ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа: 304. Абсолютная нестабильность частоты радиопередатчика Нестабильность частоты передатчика Определения термина из разных документов: Абсолютная нестабильность… … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р ИСО 5577-2009: Контроль неразрушающий. Ультразвуковой контроль. Словарь — Терминология ГОСТ Р ИСО 5577 2009: Контроль неразрушающий. Ультразвуковой контроль. Словарь оригинал документа: 2.8.2 автоматическое сканирование: Перемещение преобразователя по поверхности ввода, реализованное механическими средствами.… … Словарь-справочник терминов нормативно-технической документации

ГОСТ 24346-80: Вибрация. Термины и определения — Терминология ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа: 112. Автоколебания Колебания системы, возникающие в результате самовозбуждения Определения термина из разных документов: Автоколебания 137. Активная виброзащита… … Словарь-справочник терминов нормативно-технической документации

Источник

Упругие волны (механические волны).

Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.

Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.

Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.

Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.

Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д. Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.

Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.

В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.

Продольная волна.

Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.

В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).

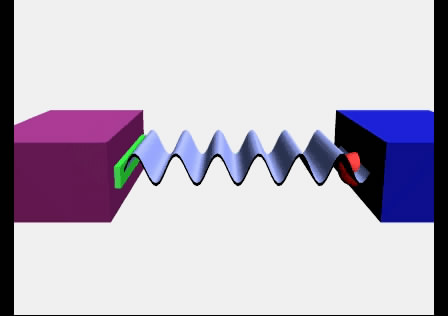
Пример распространения продольной упругой волны изображен на рисунке а и б выше. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближа­ются, возникает сила упругости, под действием которой эти витки начинают расходиться. Про­должая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение (рисунок б). При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положе­ния равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.

Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными. В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других.

Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.

Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.

В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде воли в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одина­ковыми фазами.

Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называ­ется волновой поверхностью, или фронтом волны.

С этой точки зрения плоской волне можно дать и следующее определение:

Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.

Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.

Уравнение плоской синусоидальной волны имеет вид:

где s — смещение колеблющейся точки, s_m — амплитуда колебаний, ω — циклическая частота, t — время, х — текущая координата, v — скорость распространения колебаний или скорость волны, φ₀ — начальная фаза колебаний.

Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.

Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.

Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:

.

Источник

Сферические и плоские волны

Научитесь различать сферические и плоские волны. Читайте, какую волну называют плоской или сферической, источник, роль волнового фронта, характеристика.

Сферические волны возникают из точечного источника в сферическом узоре, а плоские – бесконечные параллельные плоскости, нормальные к вектору фазовой скорости.

Задача обучения

Основные пункты

Термины

Сферические волны

Какую волну называют сферической? Разработать метод по определению способа и места распространения волн удалось Кристиану Гюйгенсу. В 1678 году он выдвинул предположение, что каждая точка, с которой сталкивается световая помеха, превращается в источник сферической волны. Суммирование вторичных волн вычисляет вид в любом времени. Этот принцип показал, что при контакте волны создают деструктивные или конструктивные помехи.

Конструктивные формируются, если волны полностью пребывают в фазе друг друга, а финальная усиливается. В деструктивных волны не соответствуют по фазам и финальная просто сокращается. Волны возникают из одного точечного источника, поэтому формируются в сферическом узоре.

Если волны генерируются из точечного источника, то выступают сферическими

Этот принцип применяет закон преломления. Каждая точка на волне создает волны, мешающие друг другу конструктивно или деструктивно

Плоские волны

Теперь давайте поймем, какую волну называют плоской. Плоская отображает частотную волну, фронты которой выступают бесконечными параллельными плоскостями со стабильной амплитудой, расположенной перпендикулярно вектору фазовой скорости. В реальности нельзя добыть истинную плоскую волну. Только плоская с бесконечной протяжностью сможет ей соответствовать. Правда, многие волны приближаются к такому состоянию. Например, антенна формирует поле, выступающее примерно плоским.

Плоские отображают бесконечное число волновых фронтов, нормальных к стороне распространения

Источник

2.5. Сферические волны

В предыдущих разделах мы рассматривали специальный тип волн: фаза

зависела только от координаты х.

Волновой фронт — это нестационарная поверхность, во всех точках которой фаза волны имеет одно и то же постоянное во времени значение.

Для изученных нами волн колебания среды одинаковы во всех точках плоскости, ортогональной направлению распространения волны (мы выбрали его в качестве оси х). Иными словами, фронт волны является плоскостью, параллельной плоскости, содержащей оси у, z. Фронт бегущей волны перемещается с течением времени вдоль оси х с фазовой скоростью v. Такие волны называются плоскими.

Трехмерное волновое уравнение

Пусть мы по-прежнему имеем дело с плоской волной. Повернем координатные оси так, чтобы направление распространения волны задавалось каким-то единичным вектором n. Решение, очевидно, имеет вид:

Соотношения между , k и остаются прежними.

Волновой вектор — это вектор, модуль которого равен волновому числу, а направление совпадает с направлением распространения волны:

Фронт волны – плоскость, ортогональная волновому вектору k, – движется со скоростью v, оставаясь параллельным самому себе.

Найдем уравнение, которому удовлетворяет решение (2.65). Дважды дифференцируем выражение (2.65) по координатам х, у, z:

Складывая эти три уравнения, находим:

Вторая производная решения по времени имеет вид:

получаем из (2.67), (2.68):

Выражение в скобках в левой части уравнения является дифференциальным оператором, который называется лапласианом (или оператором Лапласа) и имеет специальное обозначение .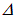

Записываем волновое уравнение для волн в трехмерном пространстве в окончательной форме:

Если волновая функция и зависит только от одной координаты (скажем, х), то лапласиан превращается во вторую производную по x, и мы возвращаемся к прежней форме волнового уравнения.

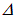
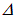
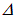
Подчеркнем, что не есть греческая буква («дельта»), а u не есть приращение величины u, но сумма вторых ее производных по координатам.

Но волновое уравнение (2.70) имеет и другие решения, нежели плоские волны. Простым дифференцированием можно убедиться, что сферическая волна

удовлетворяет волновому уравнению. Фронт волны является сферой с центром в месте расположения источника колебаний (r = 0), причем радиус сферы увеличивается со скоростью v.

Действительно, поверхность постоянной фазы дается уравнением

дифференцируя которое, находим

Амплитуда сферической волны

убывает с увеличением расстояния до точки наблюдения. Интенсивность волны

Стоя у полотна железной дороги, можно наблюдать следующее явление: сигнал приближающейся электрички резко меняет свой тон (частоту) в момент прохождения электрички мимо наблюдателя. Это же явление может заметить наблюдатель, сидящий в поезде и проезжающий мимо сигналящего автомобиля, стоящего на переезде.

На рис. 2.18 демонстрируется аналогичное явление при движении вертолета мимо наблюдателя.

Рис. 2.18. Изменение тона звука при движении вертолета мимо наблюдателя

Эффект Доплера — это изменение наблюдаемой частоты волны при относительном движении источника и/или наблюдателя.

Эффект назван по имени австрийского физика X. Доплера, предсказавшего его теоретически в 1842 г.

Движущийся наблюдатель, покоящийся источник звука. Пусть имеется источник звука, испускающий сферические звуковые волны. На рис. 2.19 показано расположение в пространстве четырех последовательных гребней (максимумов) звуковых волн. Пусть волна имеет частоту , тогда расстояние между гребнями равно длине волны

Рис. 2.19. Эффект Доплера при движении наблюдателя

Наблюдатель А движется прямо на источник звука со скоростью . Поэтому гребни волн приближаются к нему с увеличенной скоростью . С каждым последовательным гребнем волны наблюдатель встретится через время

после предыдущего. Следовательно, для него изменяется период колебаний. Наблюдаемая частота волны равна

Наблюдатель В удаляется по прямой линии от источника с той же скоростью (предполагаем, что , наблюдатель, удаляющийся от источника со сверхзвуковой скоростью, «убежит» от волны и вообще не услышит звука). Значит, гребни волн приближаются к нему со скоростью , и период колебаний равен

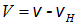
Отсюда получаем для наблюдаемой частоты:

Наконец, пусть наблюдатель Р движется со скоростью v_H, составляющей угол 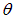с направлением на источник. На сдвиг частоты влияет только компонента скорости вдоль линии, соединяющей наблюдателя и источник:

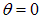
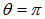
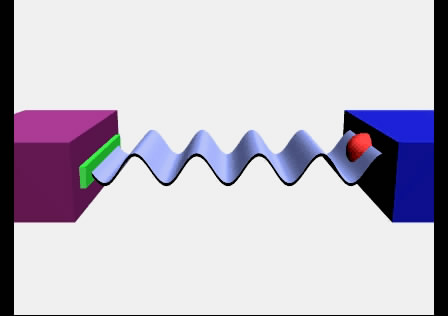
Предыдущие формулы (2.72) и (2.73) для частных случаев получаются отсюда при и , соответственно.

На рис. 2.20 с помощью модели демонстрируется эффект Доплера для случая покоящегося источника звука и движущегося наблюдателя.

Рис. 2.20. Моделирование эффекта Доплера при движении наблюдателя

Движущийся источник звука, покоящийся наблюдатель. Пусть теперь наблюдатель неподвижен, а звуковые волны испускаются источником, движущимся со скоростью 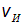. На рис. 3.21 показано расположение в пространстве четырех последовательных гребней звуковой волны, отмеченных цифрами черного цвета 1, 2, 3, 4.

Рис. 2.21. Эффект Доплера при движении источника

Эти гребни были испущены, когда источник звука находился в точках, отмеченных цифрами красного цвета 1, 2, 3, 4, соответственно. Иначе, точка 1 является центром сферы 1, точка 2 — центром сферы 2 и т. д. Видно, что центры соседних сфер смещаются на расстояние, проходимое источником за период колебаний

Это приводит к изменению расстояния между гребнями волн, приходящих к наблюдателю. Следовательно, наблюдатель регистрирует иную длину волны.

Наблюдатель А расположен так, что источник движется прямо на него. Для этого наблюдателя расстояние между гребнями волн уменьшается и равно

Скорость волны не зависит от движения источника, поскольку определяется свойствами среды. Следовательно, имеем обычную связь между длиной волны и ее фазовой скоростью:

Подставляя эти соотношения в (2.75), получаем

откуда находим частоту n звука, воспринимаемого наблюдателем А:

Для наблюдателя В расстояние между гребнями волн увеличивается и равно

Аналогичные рассуждения приводят к следующему выражению для частоты звуковой волны:

Наконец, для наблюдателя Р, направление на которого составляет угол со скоростью источника, выражение для частоты имеет вид:

Предыдущие выражения получаются отсюда при и , соответственно.

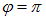
Пример 1. Наблюдатель, стоящий на платформе железной дороги, слышит гудок проходящего мимо поезда. Когда поезд приближается, частота звуковых колебаний гудка равна , а когда поезд удаляется — . Определим скорость поезда V и собственную частоту гудка . Скорость звука v предполагается известной.

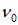
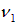
При скорости поезда V, скорости звука v и собственной частоте колебаний частота , воспринимаемая при приближении поезда, равна

При удалении поезда воспринимаемая частота звука равна

Разделив первое соотношение на второе, получаем:

Отсюда находим скорость поезда:

Подставляя скорость поезда в выражение (2.79), получаем оттуда:

На рис. 2.22 с помощью модели демонстрируется эффект Доплера в случае движущегося источника звука и покоящегося наблюдателя.

Рис. 2.22. Моделирование эффекта Доплера при движении источника

Движущийся источник звука, движущийся наблюдатель. Из полученных формул можно сделать общие выводы:

Выражение (2.84) явным образом нарушает принцип относительности Галилея. В самом деле, скорость сближения источника и наблюдателя есть сумма соответствующих проекций скоростей:

Согласно принципу относительности, все наблюдаемые эффекты должны зависеть только от 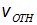. Формула же (2.84) позволяет отделить движение наблюдателя от движения источника. Для иллюстрации рассмотрим три примера. Спешим успокоить читателя: это кажущееся недоразумение, его разъяснение приведено ниже в конце рассмотрения примера 4. С принципом Галилея всё в порядке.

Пример 2. Сирена полицейской машины, стоящей на обочине дороги, издает сигнал на частоте 1 000 Гц. Определим, какой частоты звук услышит водитель, проезжающий мимо со скоростью 80 км/час.

В данном случае скорость автомобиля V = 80 км/час = 22.2 м/с — это скорость наблюдателя. Скорость звука . При сближении с полицейской машиной водитель воспринимает звук частотой

После того как водитель миновал полицейскую машину, воспринимаемая частота становится равной

Пример 3. Водитель стоящей на обочине дороги машины замечает проезжающий мимо полицейский автомобиль с включенной сиреной. Найдем частоту звука, который слышит водитель, если скорость полицейского автомобиля равна 80 км/час. Полицейская сирена – та же самая, что и в предыдущем примере.

Здесь скорость V = 22.2 м/с — это скорость движения источника. При приближении полиции водитель слышит сигнал частотой

При удалении частота воспринимаемого сигнала равна

Пример 4. Те же машины едут навстречу друг другу с равными скоростями 40 км/час = 11.1 м/с. Найдем частоты звукового сигнала при сближении и при удалении машин.

Применяем формулу (2.84). При сближении воспринимается звук частотой

При удалении машин сирена для водителя звучит на частоте

Во всех трех случаях получились разные результаты, хотя каждый раз скорости сближения (удаления) наблюдателя и источника были теми же самыми. В то же время численные результаты близки друг к другу. Это объясняется тем, что скорости автомобилей в задаче малы по сравнению со скоростью звука. В этом случае в формуле (2.84) можно пренебречь членами

и более высоких степеней. Преобразуем (2.84):

Пренебрегая теперь слагаемыми, содержащими отношения квадратов скоростей, находим приближенное выражение:

В (2.85) частота зависит только от относительной скорости источника и наблюдателя. Если бы формула была точна, во всех трех задачах мы получили бы один и тот же ответ:

Формула (2.85) удовлетворяет принципу относительности Галилея, но она верна, строго говоря, только при бесконечно большой скорости сигнала. Нарушение принципа относительности Галилея связано с наличием среды. Действительно, при движении тел в среде можно отличить состояние покоя от прямолинейного равномерного движения хотя бы по возникающему при движении ветру. Поэтому системы отсчета при наличии среды не равноправны: из них выделена та, в которой среда как целое покоится.

Рассмотрим теперь случай, когда источник звуковых волн движется со скоростью, превышающей скорость звука: . Пусть в момент времени t = 0 источник был в точке S₀, а в момент t он находится в точке S_t (рис. 2.23). Расстояние между этими точками равно .

Рис. 2.23. Образование конуса Маха при сверхзвуковом движении источника

В каждой точке своей траектории (для простоты мы рассматриваем прямолинейное равномерное движение) источник испускал сферические звуковые волны. Волна, испущенная в момент t = 0, к текущему моменту времени t достигла точки А. Волны, испущенные на пути от S₀ до S_t ,успели пройти меньшие расстояния. Как видно из рис. 2.23, в данный момент времени имеется коническая поверхность (ее называют конусом Маха), касательная к фронтам всех испущенных сферических волн. Эта коническая поверхность начинается от источника звука, а ее ось совпадает с направлением движения источника. Конус Маха отделяет области пространства, куда дошел звук от источника, от тех областей, куда звук не успел еще дойти. В следующий момент времени источник переместится в точку . Соответственно переместится и конус Маха, захватив новые области пространства (показано пунктирной линией).

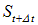
Синус угла раствора конуса определяется как отношение расстояния , пройденного звуковой волной за время t, к расстоянию , пройденного источником за то же время:

Коническую поверхность можно воспринимать как фронт волны (ее называют ударной). Направление распространения волны — это нормаль к фронту. Следовательно, ударная волна распространяется под углом

к направлению движения источника. Соответственно, (2.86) можно записать в виде:

Число Маха — это отношение , то есть скорости источника к скорости звука в данной среде.

Пример 5. Самолет летит горизонтально на высоте 5 000 м с постоянной скоростью. Наблюдатель заметил его у себя над головой, и засек время. Звук от самолета появился через 11 с после этого. Найдем скорость самолета и определим, на каком расстоянии по горизонтали находится самолет от наблюдателя в момент, когда последний зарегистрировал приход звука от него?

За время t самолет удалился от наблюдателя на расстояние 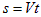. Так как в этот момент звук достиг наблюдателя, то точка наблюдения оказалась на конусе Маха (рис. 2.24).

Рис. 2.24. К примеру 5. О пролете сверхзвукового самолета. Пунктирная линия – положение конуса Маха
в момент пролета самолета над головой, сплошная – конус Маха в момент,
когда звук дошел до наблюдателя

Источник