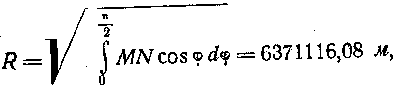Какими элементами параметрами определяется земной эллипсоид

Геодезия

Для студентов аспирантов и преподавателей

Разделы

Общий земной эллипсоид

При изучении фигуры Земли с давних пор поступают следующим образом. Сначала определяют форму и размеры некоторой модели Земли, поверхность которой сравнительно проста, хорошо изучена в геометрическом отношении, удобна для решения на ней разнообразных задач геодезии и картографии и наиболее полно характеризует в первом приближении форму и размеры реальной Земли. Затем, приняв поверхность этой модели Земли за отсчетную, определяют относительно нее высоты точек поверхности изучаемой фигуры — геоида (квазигеоида) или реальной Земли — и таким образом получают данные, характеризующие форму и размеры конкретной фигуры.

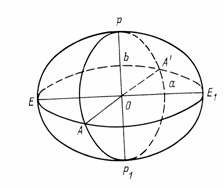
При решении задач высшей геодезии за такую модель Земли принимают эллипсоид вращения с малым полярным сжатием, называемый общим земным эллипсоидом (рис. 4). Его поверхность может быть получена вращением полуэллипса РЕР₁ вокруг его малой оси РР₁.

Форма и размеры земного эллипсоида характеризуются большой а и малой bполуосями, а чаще большой полуосью а и полярным сжатием а,

(1.10)

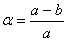
или большой полуосью а и первым эксцентриситетом е меридианного эллипса:

(1.11)

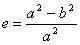
Для того чтобы общий земной эллипсоид возможно точнее характеризовал форму и размеры всей Земли, его параметры а, а определяют с учетом следующих условий:

1) центр общего земного эллипсоида должен совпадать с центром масс Земли, а его малая ось — с осью вращения Земли;

Рис. 4. Земной эллипсоид

2) объем эллипсоида должен быть равен объему геоида (квазигеоида);

3) сумма квадратов отклонений по высоте поверхности эллипсоида от поверхности геоида (квазигеоида) должна быть наименьшей.

До недавнего времени, т. е. до начала освоения человеком космического пространства, параметры земного эллипсоида получали, выполняя так называемые градусные измерения. С этой целью прокладывали ряды триангуляции по направлению меридианов и параллелей на разных широтах, на конечных пунктах которых определяли астрономические широты, долготы, а также азимуты сторон. Для вывода надежных значений параметров общего земного эллипсоида градусные измерения, в принципе, необходимо было выполнить на всей поверхности Земли, включая Мировой океан. Кроме того, астрономические широты, долготы и азимуты следовало исправить поправками за влияние уклонений отвесных линий, которые, как правило, были неизвестны.

В прошлом градусные измерения велись только на материках, т. е. на незначительной части земной поверхности. Градусные измерения разных стран не имели общих связей, выполнялись по разным программам с разной точностью, обрабатывались в разных системах координат. Все это затрудняло их совместное использование и отрицательно сказывалось на точности выводов размеров земного эллипсоида.

В течение полутора веков ученые многих стран занимались определением размеров земного эллипсоида, используя имеющиеся в разном объеме разной точности и содержания градусные измерения. Приведем некоторые результаты таких определений (табл.” 1).

Эллипсоид Деламбра имеет только лишь историческое значение как основа для установления метрической системы мер. На поверхности эллипсоида Деламбра расстояние от полюса до экватора точно составляет 10000 км, так как в то время 1 м

Источник

ЗЕМНОЙ ЭЛЛИПСОИД

§ 1. Фигура и размеры Земли

При выводе размеров референц-эллипсоида группой ученых, геодезистов, топографов и вычислителей под руководством профессора Ф. Н. Красовского были использованы обширнейшие материалы астрономических, геодезических и гравиметрических измерений, производившихся в СССР на протяжении многих лет, а также результаты аналогичных работ, выполненных в других странах. Размеры референц-эллипсоида Красовского подтверждаются также результатами обработки наблюдений за искусственными спутниками Земли, произведенных в последние годы.
Ориентирование в теле Земли земного эллипсоида с соответствующими размерами полуосей и сжатия характеризуется так называемыми исходными геодезическими датами. Исходными геодезическими датами называют координаты начального пункта триангуляции, определяющие его Широту В₀, долготу L₀, азимут A₀ на какой-либо смежный пункт и высоту h₀ поверхности геоида относительно поверхности референц-эллипсоида.
Эти даты принимаются за начальные при расчете координат всех других пунктов земной поверхности.
При- пользовании иностранными. картами следует помнить, что в разных странах приняты различные исходные геодезические даты. Поэтому одни и те же пункты на картах, изданных в разных странах, могут иметь различные координаты. Хотя это различие может быть и небольшим, но с ним в кораблевождении нужно считаться и перенос места корабля с одной карты на другую при плавании вблизи берегов следует производить не по географическим координатам, а по направлению и расстоянию до ближайшего опорного пункта, помещенного на обеих картах.
Принятие Земли за эллипсоид вращения является, по существу, вторым приближением при определении фигуры Земли. При решении некоторых задач практической навигации, не требующих высокой точности, оказывается возможным ограничиваться первым приближением в определении формы Земли — принимать Землю за шар. К таким задачам относятся вычисления дальности видимости ориентиров в море, расчеты для плавания по кратчайшему расстоянию, аналитические расчеты при определении места по радиопеленгам, расчеты по формулам аналитического счисления и некоторые другие.
Для определения величины радиуса Земли — шара обычно исходят из некоторых дополнительных условий.
Одним из них является условие, чтобы длина одной минуты дуги меридиана (или любого большого круга на шаре) была равна 1852 м, т. е. длине стандартной морской мили. В этом случае радиус шара, отвечающего поставленному условию, получится равным
R = 1852 * 60 * 360 / 2 π = 6 366 707 м.
При решении ряда задач картографии ставится условие, чтобы объем земного шара был равен объему земного эллипсоида или чтобы поверхность шара была равна поверхности эллипсоида. Длина радиуса R шара, одинакового с земным эллипсоидом объема, равна
R = кубический корень √ (a 2 * b) = 6371109,7 м.
Если ставится условие, чтобы поверхность шара была равна поверхности эллипсоида, то радиус такого шара принимается равным

где М— радиус кривизны меридиана; N — радиус кривизны первого вертикала в данной точке.

§ 2. Географическая система координат

§ 3. Разность широт и разность долгот

Источник

Понятие о земном эллипсоиде и сфере

Известно, что Земля шарообразна, т.е. не обладает формой идеального шара. Фигура ее неправильна, и, как всякое вращающееся тело, она немного сплюснута у полюсов. Кроме того, из-за неравномерного распределения масс земного вещества и тектонических деформаций Земля имеет обширные выпуклости и вогнутости. В силу этого земную поверхность заменяют некоторой правильной поверхностью, которая носит название поверхности относимости.

В самом точном приближении такой поверхностью является поверхность геоида (фигура, ограниченная уровенной поверхностью океана). Точно определить его форму практически невозможно. Поэтому в теории и практике картографии за поверхность относимости принимают земной эллипсоид, либо сферу определенного радиуса (при создании мелкомасштабных карт (когда можно пренебречь полярным сжатием).

Земной эллипсоид – это эллипсоид вращения с малым сжатием, размеры которого выбраны таким образом, чтобы для заданной территории он наименее уклонялся от геоида. При этом полагают, что плоскость экватора и центр эллипсоида вращения совпадают с плоскостью экватора и центром масс Земли. Такой земной эллипсоид иначе называют референц-эллипсоидом.

Постановлением Совета Министров от 7 апреля 1946 г. за такой референц-эллипсоид у нас в стране принят референц-эллипсоид Красовского. Он имеет следующие параметры:

a = 6 378 245 км – большая полуось;

b = 6 356 863 км – малая полуось;

с = 1 : 298,3 – полярное сжатие.

Рис.1. Эллипсоид вращения и его элементы

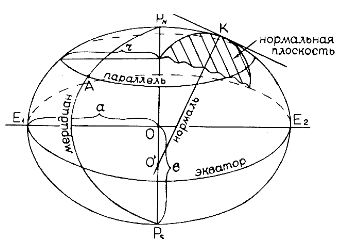
Эллипсоид вращения образуется вращением эллипса P_NE₁P_SE₂ вокруг полярной оси P_NP_S (рис. 1). Точки P_N, P_S являются, соответственно, северным и южным полюсами эллипсоида. Они получаются сечением оси P_NP_S поверхности эллипсоида.

Сечения поверхности эллипсоида вращения плоскостями, параллельными плоскости экватора, образуют окружности – параллели. Сечения поверхности эллипсоида вращения плоскостями, проходящими через ось вращения, образуют эллипсы – меридианы.

Пусть О’К’ – нормаль к поверхности эллипсоида в точке К (рис. 1). Плоскости, проходящие через нормаль, называются нормальными плоскостями. Сечения этих плоскостей с поверхностью эллипсоида дают нормальные сечения, или вертикалы. Тогда меридиан – это нормальное сечение, плоскость которого проходит через полярную ось. Нормальное сечение, перпендикулярное плоскости меридиана P_NЕ₁P_SЕ₂, дает сечение 1-го вертикала.

Радиусы кривизны этих сечений определяются следующими формулами:

– радиус кривизны меридиана;

– радиус кривизны 1-го вертикала;

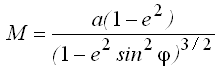
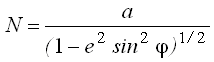
где 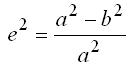– 1-й эксцентриситет;

a и b – большая и малая полуоси эллипсоида вращения.

Радиус параллели (r) вычисляется через радиус кривизны первого вертикала

Источник

Земной эллипсоид, его основные параметры и соотношения между ними.

Основной задачей геодезии является изучение реально существующей физической поверхности Земли и ее внешнего гравитационного поля. Эта задача решается на основе математической обработки результатов спутниковых, астрономических, геодезических и гравиметрических измерений. По измеренным на земной поверхности углам и расстояниям вычислить с высокой точностью координаты точек не возможно, т.к. неизвестен вид сложной физической поверхности Земли. Целью измерений является определение поверхности. Поэтому в геодезии при решении задач, связанных с математической обработкой наземных измерений, вводится вспомогательная координатная поверхность, которая должна быть наиболее близкой по форме и размерам к действительной поверхности Земли и иметь достаточно простой математический вид, чтобы без затруднений выполнять на ней математическую обработку измерений. В качестве такой поверхности принята поверхность эллипсоида вращения, которая называется общим земным эллипсоидом.

Эллипсоид вращения получен путем вращения эллипса вокруг малой оси. Два основных параметра эллипса: большая полуось а=ОЕ, малая полуось в=ОР.

Полярное сжатие Квадрат первого эксцентриситета Квадрат второго эксцентриситета

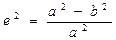
Связь ; ; Параметры эллипсоида: а=6378245м, =1/298.9, 1/150.

Геодезическая параллель – линия пересечения поверхности эллипсоида вращения и плоскости перпендикулярной оси вращения. Если плоскость сечения проходит через центр эллипсоида, то геодезическая параллель называется экватором. Геодезический меридиан – часть линии пересечения поверхности эллипсоида вращения и плоскости, содержащей ось вращения, заключенной между полюсами. Все меридианы одинаковы и являются половинками эллипсов. Для того чтобы задать эллипсоид, нужно задать 2 параметра, один из которых должен быть линейным, а остальные можно вычислить.

Система прямоугольных пространственных координат

За начало координат в этой системе принимается центр эллипсоида – О. Ось OZ направлена по полярной оси, ось ОХ расположена по линии пересечения плоскости Гринвичского меридиана и плоскости экватора

Ось OY дополняет систему до правой. Тогда положение точки Q на поверхности эллип­соида будет определено однозначно координатами:

Достоинства: 1. Координаты XYZ однозначно определяют положение точки в пространстве. 2. Для ее применения не нужен эллипсоид вращения.

Недостатки: 1. Нельзя разделить XYZ. 2. Основная система координат – система плоских прямоугольных координат, но прямого перехода от XYZ к XY – нет.

Данная система применяется в выводах формул для обработки спутниковых наблюдений.

Система геодезических координат.

В этой системе координат положение точки в пространстве определяется тремя координатами:

Геодезическая долгота – это двугранный угол, составленный плоскостью начального геодезического меридиана и плоскостью геодезического меридиана проходящего через заданную точку.

Долгота измеряется от 0 до 360 0 или от 0 до 180 0 на восток и запад от гринвичского меридиана. Но долгота определяет положение меридиана, проходящего через точку, а не саму точку.

Для определения положения точки на меридиане используется широта.

Геодезическая широта – это острый угол составленный плоскостью экватора и нормалью к поверхности эллипсоида, проходящей через заданную точку.

Геодезическая высота – отрезок нормали от эллипсоида до точки.

Достоинства:1. Координаты BLH однозначно определяют положение точки в пространстве. 2. Эта с.к. позволяет общую задачу по вычислению координат пунктов разделить на 2 подзадачи меньшей размерности. Отдельно определяют BL, отдельно Н. 3. эта система координат связана с системой плоских прямоугольных координат, которая является основной.

Билет 22

Преобразование плоских прямоугольных координат Гаусса-Крюгера из одной зоны в другую

Задача по преобразованию координат Гаусса-Крюгера возникает в двух случаях:

1.Когда геодезические работы выполняются на границе двух зон.

Когда возникает необходимость перехода от 6º к 3º зонам или к зонам с частным началом координат.

Существует 3 способа преобразования координат:

Исходные данные: х (1) ; у (2) ; L₀ (1) (n (1) ); L₀ (2) (n (2) )

1.Аналитический способ: путем последовательного перехода.

1. Способ универсальный

2. Способ точный, если использовать соответствующие формулы

3. Вычисления можно автоматизировать

Недостаток:Если нет компьютера.

2.Табличный способ: основан на применение специальных таблиц для преобразования прямоугольных координат.

Этим способом можно решить 3 задачи (при использовании таблиц):

1.Из 6º зоны преобразовать координаты в 3º

2.Из 3 зоны преобразовать координаты в 6º

3.Из 6º зоны преобразовать координаты в 6º

Недостаток: Невозможна автоматизация Выполняются преобразования координат из государственной в государственную систему.

3.Графический способ: можно применять в зонах взаимного перекрытия (30′ в каждой зоне).

Недостатки:Применяются в зонах взаимного перекрытия. Низкая точность способа, которая зависит от масштаба.

Источник

Учебник по навигации

Глава 1

§ 1. Фигура и размеры Земли

При выводе размеров референц-эллипсоида группой ученых, геодезистов, топографов и вычислителей под руководством профессора Ф. Н. Красовского были использованы обширнейшие материалы астрономических, геодезических и гравиметрических измерений, производившихся в СССР на протяжении многих лет, а также результаты аналогичных работ, выполненных в других странах. Размеры референц-эллипсоида Красовского подтверждаются также результатами обработки наблюдений за искусственными спутниками Земли, произведенных в последние годы.
Ориентирование в теле Земли земного эллипсоида с соответствующими размерами полуосей и сжатия характеризуется так называемыми исходными геодезическими датами. Исходными геодезическими датами называют координаты начального пункта триангуляции, определяющие его Широту В₀, долготу L₀, азимут A₀ на какой-либо смежный пункт и высоту h₀ поверхности геоида относительно поверхности референц-эллипсоида.
Эти даты принимаются за начальные при расчете координат всех других пунктов земной поверхности.
При- пользовании иностранными. картами следует помнить, что в разных странах приняты различные исходные геодезические даты. Поэтому одни и те же пункты на картах, изданных в разных странах, могут иметь различные координаты. Хотя это различие может быть и небольшим, но с ним в кораблевождении нужно считаться и перенос места корабля с одной карты на другую при плавании вблизи берегов следует производить не по географическим координатам, а по направлению и расстоянию до ближайшего опорного пункта, помещенного на обеих картах.
Принятие Земли за эллипсоид вращения является, по существу, вторым приближением при определении фигуры Земли. При решении некоторых задач практической навигации, не требующих высокой точности, оказывается возможным ограничиваться первым приближением в определении формы Земли — принимать Землю за шар. К таким задачам относятся вычисления дальности видимости ориентиров в море, расчеты для плавания по кратчайшему расстоянию, аналитические расчеты при определении места по радиопеленгам, расчеты по формулам аналитического счисления и некоторые другие.
Для определения величины радиуса Земли — шара обычно исходят из некоторых дополнительных условий.
Одним из них является условие, чтобы длина одной минуты дуги меридиана (или любого большого круга на шаре) была равна 1852 м, т. е. длине стандартной морской мили. В этом случае радиус шара, отвечающего поставленному условию, получится равным
R = 1852 * 60 * 360 / 2 &#960 = 6 366 707 м.
При решении ряда задач картографии ставится условие, чтобы объем земного шара был равен объему земного эллипсоида или чтобы поверхность шара была равна поверхности эллипсоида. Длина радиуса R шара, одинакового с земным эллипсоидом объема, равна
R = кубический корень &#8730 (a 2 * b) = 6371109,7 м.
Если ставится условие, чтобы поверхность шара была равна поверхности эллипсоида, то радиус такого шара принимается равным

Источник