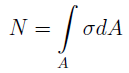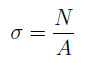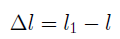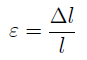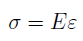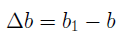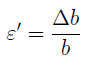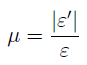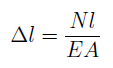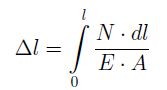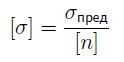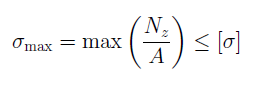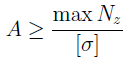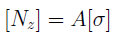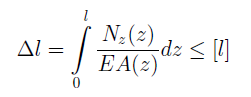Какими параметрами может характеризоваться растяжение и сжатие
Сопротивление материалов. Шпаргалка для студентов
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов предоставлен нашим книжным партнёром — компанией ЛитРес.
5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации
Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот — длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения — поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε’ — деформации, приходящиеся на единицу длины или пощади сечения стержня.
где Δl — изменение длины стержня;
Δa — изменение площади сечения.
Продольную деформацию растяжения обычно считают положительной, деформацию сжатия — отрицательной. Продольная и поперечная деформации связаны соотношением
μ — коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.
В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.
Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости — это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.
Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:
Произведение EA называется жесткостью сечения.
При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.
Растяжение и сжатие
Растяжением (сжатием) называется такой вид деформации, при котором в любом поперечном сечении стержня возникает только продольная растягивающая (сжимающая) сила.
При такой деформации вводятся следующие допущения: поперечные сечения стержня плоские и нормальные к его оси до деформации остаются плоскими и нормальными после деформации — гипотеза плоских сечений, или гипотеза Бернулли.
В соответствии с этой гипотезой в поперечном сечении возникают только нормальные напряжения, равномерно распределенные по сечению:
где N— продольная сила; F— площадь поперечного сечения.
Для нахождения нормальных напряжений и продольных сил удобно пользоваться графиками (эпюрами).
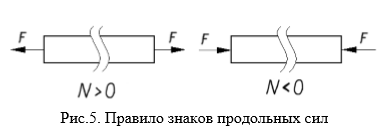
При этом считают, что продольная сила при растяжении имеет знак «плюс», а при сжатии — знак «минус».
Рассмотрим деформации стержня.
Под действием осевых растягивающих сил стержень удлиняется на
где /, /0 — длины стержня соответственно в деформированном и не- деформированном состояниях. Это приращение длины называется абсолютным или полным удлинением.
Более удобно деформации определять при помощи относительного удлинения, т.е. удлинения, отнесенного к длине стержня:
Это выражение называется линейной деформацией и обычно выражается в процентах начальной длины.
При деформации возникает не только продольная деформация, но и поперечная. Отношение поперечной деформации к продольной называется коэффициентом Пуассона
Закон Гука при растяжении и сжатии. Нормальное напряжение пропорционально относительному удлинению или укорочению
где Е— модуль упругости, характеризующий жесткость материала.
Абсолютное удлинение или сжатие пропорционально продольной силе, длине и обратно пропорционально жесткости сечения:
При нагружении конструкций определяют предельные напряжения, при которых происходит нарушение работы конструкции или ее разрушение.
Предельным напряжением для пластичных материалов является предел текучести, для хрупких — предел прочности.
Отношение предельного напряжения к напряжению, возникающему в процессе работы, называется коэффициентом запаса прочности:
Сечение, для которого коэффициент запаса прочности наименьший, является опасным.
Минимально необходимый коэффициент запаса прочности называется допускаемым [п]. Так, для пластичных материалов [п] = 1,4 — 2,5; для хрупких [п] = 2,5 — 5; для дерева [лг] = 8 — 12.
Отношение предельного напряжения к допускаемому коэффициенту запаса прочности называется допускаемым напряжением:
Оценка прочности стержня проводится по условию прочности:
Основные типы задач на растяжение (сжатие):
3) определение допускаемой продольной силы — проводится по заданным поперечным размерам и известному допускаемому напряжению
Техническая механика
Сопротивление материалов
Растяжение и сжатие
Напряжения и характер деформаций при растяжении и сжатии
При определении величины продольной силы алгебраическим сложением внешних сил следует обращать внимание на знаки (векторные значения) этих сил. При расчетах в сопромате обычно принимают растягивающие нагрузки (направленные от сечения) положительными, а сжимающие – отрицательными.
Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:
Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:
где N – продольная сила, А – площадь поперечного сечения бруса.
По эпюрам, представленным на рис. 2 можно заметить, что в местах приложения внешних нагрузок и реакций внутренние силовые факторы изменяются скачкообразно (принцип Сен-Венана).
Визуальное исследование эпюры позволяет определить критические участки бруса, находящиеся в наиболее напряженном состоянии. Так, по представленным на рис. 2 эпюрам напряжений, возникающих в брусе, можно определить, что критическим является 2-й участок, поскольку здесь возникает наибольшее напряжение (по эпюре видно, что это напряжение сжатия, т. к. оно имеет отрицательное значение).
Кроме того, эпюра любого силового фактора позволяет (без применения лишних расчетов) определить силу или момент, действующие на брус со стороны, например, заделки, поскольку после построения эпюры со стороны свободного конца бруса эти силовые факторы отобразятся графически, без вычислений.
Ниже размещен видеоролик, в котором подробно объясняется порядок построения эпюр продольных сил и напряжений, возникающих в брусе при растяжении и сжатии, а также выводы, которые можно сделать на основе визуального анализа графиков.
Видеоурок ведет преподаватель ГОУ СПО «Нижнетагильский горно-металлургический колледж» Чирков А. С.
Материалы раздела «Растяжение и сжатие»:
Растяжение-сжатие.
Внутренние усилия при растяжении-сжатии.
Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
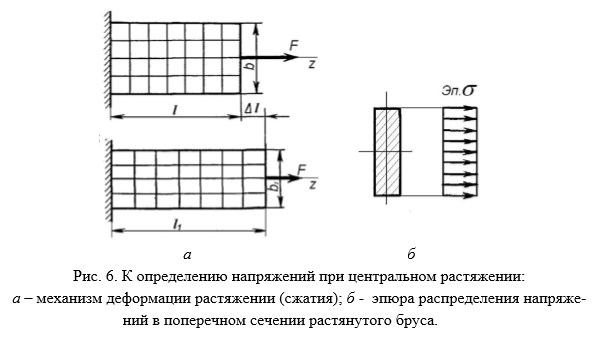
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.
Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
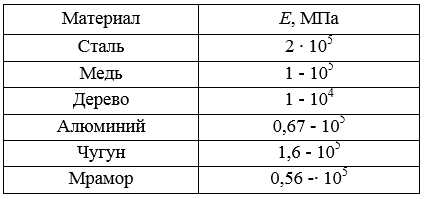
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Модуль продольной упругости для различных материалов
Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε ‘ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε ‘ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
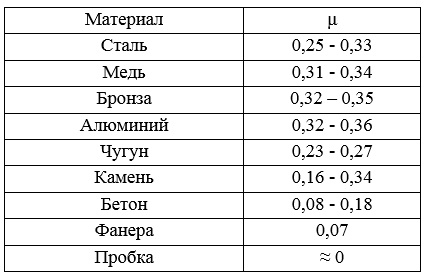
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
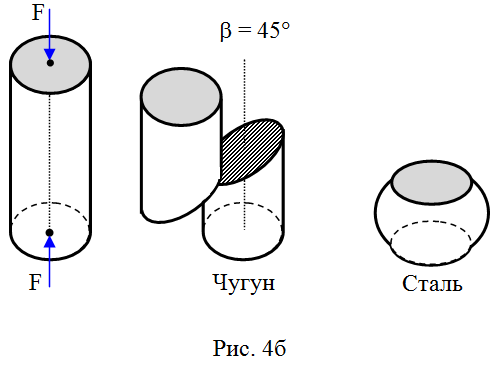
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
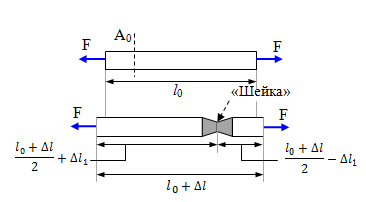
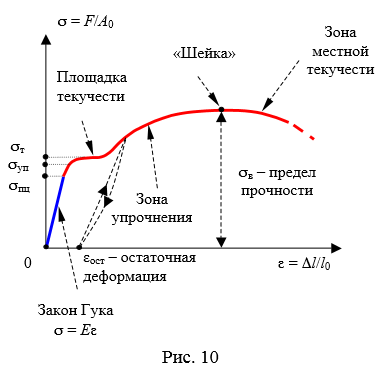
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.
Диаграмма сжатия стержня имеет вид (рис. 10, а)
Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Тема 2.2. Растяжение и сжатие
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
В случаях, когда рабочее напряжения значительно ниже допускаемых σ