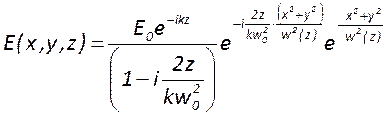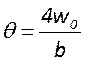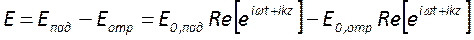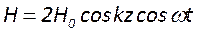Конфокальный параметр гауссова пучка

В таблице приведены конфигурации наиболее известных типов резонаторов и их названия.

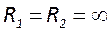
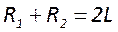
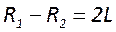
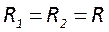
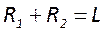
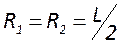
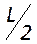
Наиболее распространены 3 конфигурации – плоскопараллельная, конфокальная и концентрическая. Для плоскопараллельной конфигурации и она всегда симметрична. Для конфокальной и она образуется совмещением фокусов зеркал. Если одно из зеркал, например второе, является выпуклым, то условие конфокальности принимает вид и общий фокус выносится за пределы резонатора, который тогда называется телескопическим. При конфокальный резонатор становится симметричным. Если одно из зеркал заменить на плоское и поместить его фокусе другого, то такой резонатор будет называться полуконфокальным. При совмещении центров кривизны зеркал выполняется условие и резонатор становится концентрическим. При концентрический резонатор превращается в симметричный и называется сферическим, так как в этом случае поверхности его зеркал лежат на одной и той же сфере радиуса. Все другие конфигурации следует считать произвольными

2. Гауссов пучок и его характеристики

Гауссовым называется такой лазерный пучок, который описывается функцией Гаусса. К таким пучкам относятся все, работающие на основной моде. Их особенностью является то, что гауссов пучок преобразуется идеальной тонкой линзой в гауссов же пучок, но с другими параметрами.

Описываются же гауссовы пучки следующими параметрами

Распределение поля гауссова пучка описывается формулой

А распределение интенсивности – формулой

, где , и значения соответствующих величин в точке , а — значение в плоскости . Проведем в некоторой точке плоскость, перпендикулярную оси пучка. Тогда — радиус пятна пучка в этой плоскости. На расстоянии от оси пучка напряженность падает в а интенсивность в раз. Поверхность одинаковых значений интенсивности, проведенная на расстоянии от пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности однополосного гиперболоида вращения. Наиболее узкий участок каустики называется её перетяжкой, а — радиусом перетяжки. Для описания гауссовых пучков также вводят параметр — конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов которого в 2 раза больше площади его перетяжки. Другие характеристики, определяемые для всех видов пучков – радиус кривизны волнового фронта и расходимость луча

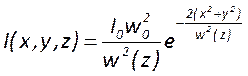
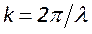
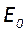
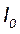
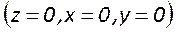
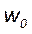
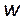
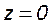
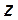
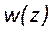
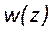
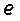
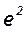
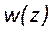
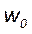
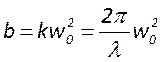
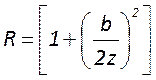
1. Устойчивость работы резонаторов. Условие устойчивости и его анализ

Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. Это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствие потерь, излучение могло бы существовать бесконечно долго. В неустойчивом резонаторе световые пучки в результате последовательных отражений от зеркал перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.

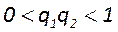
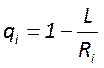
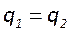
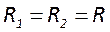
Условие устойчивости работы резонатора может быть записано в виде, где — обобщенные параметры резонатора. На рисунке это условие представлено в графическом виде в q-координатах, что позволило наглядно представить область устойчивой и неустойчиво работы резонатора. График позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов. Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной плоскости и рассматривают те типы резонаторов, параметры которых соответствуют точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение равенства , из которого следует равенство , то соответствующие резонаторы называются симметричными. При анализе графика можно сделать следующие выводы

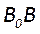
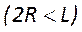
1. В области отрезка диаметр кривизны зеркал резонатора всегда меньше его длины , поэтому такой тип резонатора всегда будет неустойчивым, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

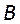
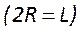
2. В точке диаметр кривизны поверхности равен длине резонатора . Здесь резонатор становится устойчивым концентрическим

3. В точке 0 мы имеем устойчивый симметричный конфокальный резонатор

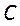
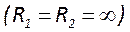
4. В точке зеркала становятся плоскими, что соответствует устойчивому плоскопараллельному резонатору.

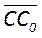
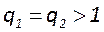
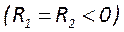
5. Точки, лежащие на отрезке , соответствуют симметричным резонаторам с выпуклыми зеркалами, так как в этой области что соответствует . Это область неустойчивой работы, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

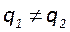
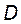
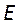
6. Для несимметричных резонаторов и соответствующие им точки лежат вне биссектрисы. При этом каждому несимметричному резонатору соответствуют две точки, которые расположенные симметрично относительно биссектрисы, и которые переходят друг в друга при перестановке зеркал. Например, точки соответствуют полуконфокальным резонаторам, а точки — полуконцентрическим

Таким образом за исключением конфокального телескопического резонатора все основные типы конфигураций относятся к устойчивым резонаторам.

2. Формирование стоячих волн в резонаторе. Моды резонатора

Рассмотрим условие, при котором в резонаторе возможно формирование стоячей волны.

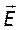
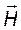
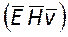
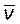
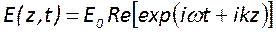
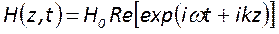
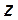
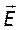
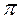
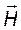
Как известно в бегущей волне векторы и совпадает по фазе, причем для нее, всегда выполняется правило правого винта , где — вектор скорости волны. Представим изменение амплитуд векторов полей это волны в виде ; . Пусть эта волна распространяется внутри резонатора таким образом, что вектор её скорости совпадает с осью . Поскольку показатель преломления отражающих поверхностей зеркал всегда больше показателя преломления граничащей с ним внутрирезонаторной среды, то, как известно при отражении от таких поверхностей вектор меняет фазу на , а вектор не меняет совсем. Тогда чтобы выполнялось правило правого винта, эти вектора при отражении от зеркал должны быть направлены так, как показано на рисунке.

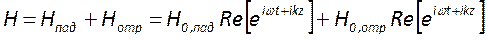
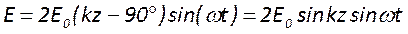
Таким образом, внутри резонатора поле в каждой точке определяется суммой прямой и обратной волн . Преобразование этих выражений приводит к следующим формулам: ,

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Распространение Гауссова пучка: понятие перетяжки пучка, глубины фокусировки, качества пучка, расходимости

Гауссов пучок

Гауссово распределение симметрично убывает по мере удаления от центра пятна (центра интенсивности, проиллюстрировано на рис. 1). Формула распределения:

(1)

Рисунок 1. Вид пятна сфокусированного пучка лазерного пучка,перетяжкой пучка называется минимальный диаметр пучка, интенсивность в пределах которого составляет не ниже 13.5% максимального значения

Профиль интенсивности не остается постоянным при распространении пучка в пространстве, следовательно, есть зависимость перетяжки (минимального диаметра) w(z) от траектории распространения z. Из-за дифракции Гауссов пучок будет уменьшаться и увеличиваться в диаметре.

Пучок сходится и расходится одинаково по обе стороны от диаметра перетяжки пучка на угол расходимости θ (рис. 2). Диаметр перетяжки пучка и угол расходимости отсчитываются от основной оси z, их связь показана уравнениями (2) и (3):

(2)

(3)

Рисунок 2. Гауссов пучок и основные параметры, применяемые для его описания: диаметр перетяжки пучка w ₀ , рэлеевская длина перетяжки z _R , угол расходимости θ

Изменение минимального диаметра пучка определяется как:

(4)

(5)

Рэлеевская длина перетяжки определяется как разность между координатами распространения, где площадь поперечного сечения пучка удваивается. Другими словами, когда диаметр перетяжки w(z) увеличивается в √2 раз. Используя уравнение (5), длину перетяжки z _R можно выразить как:

(6)

Тогда для диаметра перетяжки w(z) можно вывести следующее:

(7)

Волновой фронт излучения считается плоским в месте перетяжки пучка и квазиплоским в области бесконечно удаленной от перетяжки. Близ перетяжки радиус кривизны волнового фронта приближается к бесконечности, по мере удаления от перетяжки снова уменьшается до минимального значения.

Минимум радиуса кривизны приходится на длину Рэлея. Далее радиус кривизны снова увеличивается, а на бесконечности вновь считается плоским. Это верно для любого направления от перетяжки пучка.

Рисунок 3. Кривизна волнового фронта Гауссова пучка стремится к нулю как в положении, близком к области перетяжки, так и на дальнем расстоянии от нее

Манипуляции с Гауссовыми пучками

Зачастую в лазерной оптической системе требуется произвести некоторые манипуляции с излучением, отфильтровать, коллимировать или сфокусировать пучок. Конечно, для этого применяются различные оптические компоненты – линзы, пластины, призмы, зеркала, и т. д. Ниже приведены самые распространенные схемы включения оптики в оптический путь и основные формулы для расчета.

Уравнение тонкой линзы

Идеальная тонкая линза описывается известным уравнением геометрической оптики:

(8)

(9)

(10)

Рисунок 4. Тонкая линза: положение изображения легко определить при известном фокусном расстоянии и расстоянии от линзы до объекта

Как известно, Гауссовы пучки сохраняют профиль интенсивности после прохождения через идеальную линзу без аберраций. В 1983 году Сидни Селф записал уравнение тонкой линзы с учетом уравнения Гауссова пучка:

(11)

Общее расстояние от лазера до диаметра перетяжки рассчитывается путем прибавления абсолютного значения s к s‘. Уравнение (11) также можно записать в безразмерной форме, умножив обе стороны на f:

(12)

Это уравнение превращается в «привычное» уравнению тонкой линзы, когда соотношение z _R /f приближается к 0. Так, стандартное уравнение для тонких линз применимо для объективов с большим фокусным расстоянием. Уравнения (11) и (12) можно использовать для определения местоположения перетяжки пучка после того, как получено изображение (рис. 5).

|
Рисунок 5. Вид «изображения» и «объекта» при прохождении Гауссова пучка через тонкую линзу

График нормированного расстояния до изображения s‘/f в зависимости от нормированного расстояния до объекта s/f показывает возможные местоположения перетяжки выходного пучка в данном нормированном диапазоне Рэлея z _R /f) (рис. 6). График показывает, что Гауссовы пучки, сфокусированные тонкой линзой, имеют несколько ключевых отличий по сравнению с обычными изображениями в тонких линзах.

При рассмотрении графиков преломления Гауссова пучка в тонкой линзе можно заметить, что есть как минимальное, так и максимально возможное расстояние до изображения. При рассмотрении предметов и изображений в тонкой линзе такой параметр отсутствует. Максимальное расстояние до изображения Гауссова пучка (расстояние от линзы до диаметра перетяжки выходного пучка) достигается на расстоянии объекта, равном – (f + z _R ), а не на – f.

Точка на графике, где s/f равно – 1, а s‘/f равно 1, указывает на то, что перетяжка выходного пучка будет находиться в заднем фокусе линзы, если входное излучение подается в передней фокальной плоскости положительной линзы.

Рисунок 6. На графиках нормированных функций показано минимальное и максимальное расстояние до изображения, обусловленное наличием рэлеевской длины перетяжки

Чтобы определить положение перетяжки пучка и длину Рэлея после прохождения пучка через линзу, необходимо знать увеличение системы α, определяемое как:

(13)

(14)

Вышеупомянутое уравнение нарушится, если линзу расположить на координате, совпадающей с положением перетяжки пучка (s = 0).

Обратное значение квадрата постоянной увеличения можно использовать для определения соотношения размеров и координат перетяжки пучка:

(15)

Фокусировка Гауссова пучка в пятно

Во многих приложениях, например, в лазерной обработке материалов, медицине, очень важно фокусировать лазерный пучок в пятно минимально возможного радиуса, чтобы максимизировать интенсивность и минимизировать площадь нагрева. В таких приложениях цель состоит в том, чтобы минимизировать радиус перетяжки пучка на выходе w ₀ ‘ (рис. 7). Тогда несколько видоизмененное уравнение (15) можно применить для вычисления необходимого диаметра перетяжки:

(16)

Рисунок 7. Фокусировка пучка лазерного излучения в пятно минимально возможных размеров, например, в приложениях лазерной сварки и маркировки

(17)

(18)

Решение относительно диаметра перетяжки:

(19)

(20)

(21)

(22)

(23)

Рисунок 8. В случае двукратного увеличения перетяжка выходного пучка будет в два раза превышать перетяжку входного, это же верно и для угла расходимости пучка

Существуют два предельных случая, которые еще более упрощают расчеты размера и местоположения перетяжки выходного пучка:

В первом предельном случае уравнение (20) упрощается до:

(24)

Это также облегчает вычисления диаметра перетяжки выходного пучка, угла расходимости, длины Рэлея и положения перетяжки:

(25)

(26)

(27)

(28)

(29)

Диаметр перетяжки выходного пучка рассчитывается по формуле:

(30)

Аналогичные упрощения формул расчета, когда s _R :

(31)

(32)

(33)

(34)

Оба эти результата интуитивно понятны, поскольку волновой фронт принят почти плоским как на ближнем расстоянии от перетяжки, так и на бесконечном удалении от него. В этих местах пучок почти полностью коллимирован (рис. 9). В соответствии с известным уравнением для тонких линз параллельный входной пучок будет создавать изображение на расстоянии, равном фокусному расстоянию линзы.

Рисунок 9. Фокусировка лазерного пучка в пятно при прохождении через тонкую линзу: пятно находится в фокальной плоскости линзы, если линзу расположить: а) близ перетяжки пучка, б) на бесконечности от минимального диаметра

Смещение фокуса

Если перетяжка совпадает с плоскостью цели, то наблюдается совершенно обратная ситуация. В таком случае интенсивность сфокусированного пучка на цели, расположенной на фиксированном расстоянии L от линзы не растет.

Интенсивность фокального пятна на цели максимальна, когда от перетяжки до плоскости объекта есть некоторое расстояние (рис. 10). Это явление называется смещением фокуса.

Рисунок 10. Наибольшая интенсивность пятна излучения на цели достигается, когда перетяжка сфокусированного пучка находится в определенном месте перед мишенью, но не совпадает с плоскостью цели

Опуская вывод формул, радиус пятна излучения на цели можно описать следующим выражением:

(35)

Дифференцируя уравнение (35) относительно фокусного расстояния линзы f и решая дифференциальное уравнение относительно f, найдем частное решение при условии равенства производной функции w _L (f) по f нулю. Это показывает фокусное расстояние линзы, которое необходимо для достижения минимального радиуса пучка и, следовательно, максимальной интенсивности при падении на цель.

(36)

(37)

При |s|, стремящемся к нулю или бесконечности, производная по f функции w _L (f) равна 0, когда f = L. В обоих этих случаях входной пучок практически параллельный, из чего следует, что наименьший радиус пучка будет располагаться в фокусе линзы.

Коллимация Гауссова пучка

В реальности получить полностью параллельный пучок невозможно, так как невозможно добиться нулевой расходимости, поэтому на практике используют «практически параллельные» пучки лучей. Либо сводится к минимуму расхождение, либо увеличивается расстояние между точкой наблюдения и ближайшей перетяжкой пучка. Поскольку расходимость выходного пучка обратно пропорциональна константе увеличения α, выходная расходимость минимальна, когда |s| = f (рис. 11).

Рисунок 11. Чтобы преобразовать Гауссов пучок в параллельный, расстояние от перетяжки до коллимирующей линзы должно равняться фокусному расстоянию

Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Edmund Optics на территории РФ

Источник