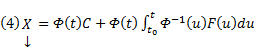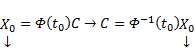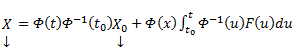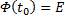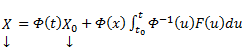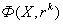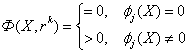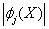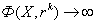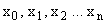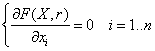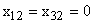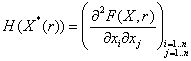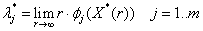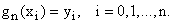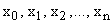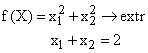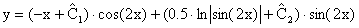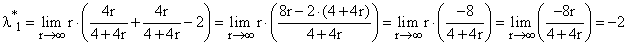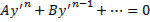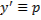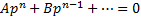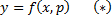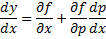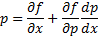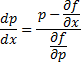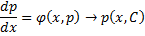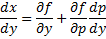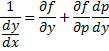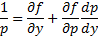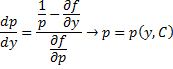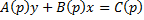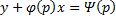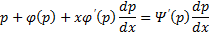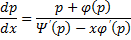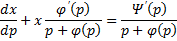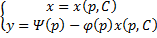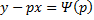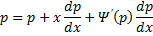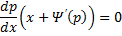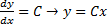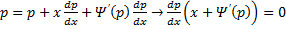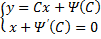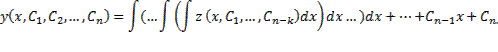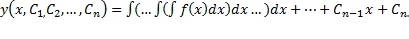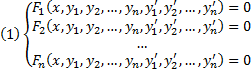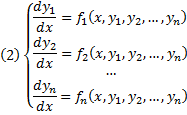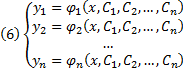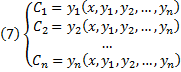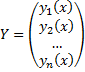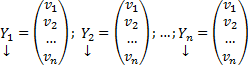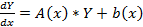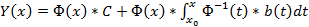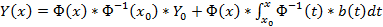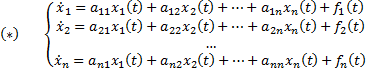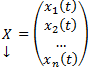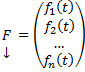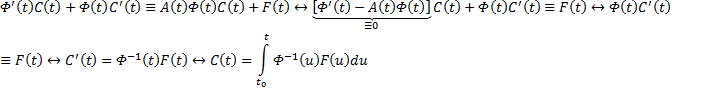Метод введения параметра дифференциальные уравнения

Метод введения параметра дифференциальные уравнения

В этом случае переменная \(x\) выражается явно через переменную \(y\) и ее производную \(y’.\) Введем параметр \(p = y’ = <\large\frac<><>\normalsize>.\) Продифференцируем уравнение \(x = f\left( \right)\) по переменной \(y.\) Получаем: \[\frac<><> = \frac<>\left[ \right)> \right] = \frac<<\partial f>><<\partial y>> + \frac<<\partial f>><<\partial p>>\frac<><>.\] Поскольку \(<\large\frac<><>\normalsize> = <\large\frac<1>

\normalsize>,\) то последнее выражение можно переписать в виде: \[\frac<1>

= \frac<<\partial f>><<\partial y>> + \frac<<\partial f>><<\partial p>>\frac<><>.\] Получаем явное дифференциальное уравнение, общее решение которого описывается функцией \[g\left( \right) = 0,\] где \(C\) − произвольная постоянная.

Таким образом, общее решение исходного дифференциального уравнения определяется в параметрической форме системой двух алгебраических уравнений: \[\left\< \begin g\left( \right) = 0\\ x = f\left( \right) \end \right..\] Если из этой системы исключить параметр \(p,\) то общее решение можно выразить в явном виде \(x = f\left( \right).\)

Уравнение такого типа не содержит переменную \(x\) и решается аналогичным образом. Используя параметр \(p = y’ = <\large\frac<><>\normalsize>,\) можно записать: \(dx = \large\frac<>

\normalsize.\) Отсюда следует, что \[dx = \frac<>

= \frac<1>

\frac<><>dp.\] Интегрируя последнее выражение, получаем общее решение исходного дифференциального уравнения в параметрической форме: \[\left\< \begin x = \int <\frac<1>

\frac<><>dp> \\ y = f\left( p \right) \end \right..\]

Это уравнение относится к типу \(x = f\left( \right)\) (Случай \(3\)). Введем параметр \(p = y’\) и запишем уравнение в виде: \[x = \frac<9><4>.\] Возьмем дифференциалы обеих частей уравнения: \[dx = \frac<9> <4>\cdot 2pdp = \frac<9><2>pdp.\] Поскольку \(dy = pdx,\) то последнее выражение можно представить как \[\frac<>

= \frac<9><2>pdp,\;\; \Rightarrow dy = \frac<9><2>dp.\] Интегрируя, находим зависимость переменной \(y\) от параметра \(p:\) \[ <2>dp> = \frac<9><2>\int <dp> > = <\frac<9> <2>\cdot \frac<<>> <3>+ C > = <\frac<3><2>+ C,> \] где \(C\) − произвольная постоянная.

Таким образом, мы получили общее решение уравнения в параметрической форме: \[\left\< \begin y = \frac<3><2>+ C\\ x = \frac<9><4>\end \right..\] Параметр \(p\) можно исключить из системы уравнений. Из второго уравнения находим: \[ <= \frac<4><9>x,>\;\; <\Rightarrow p = \pm \frac<2><3><2>\normalsize>>.> \] После подстановки в первое уравнение получаем общее решение в виде явной функции \(y = f\left( x \right):\) \[ <2><\left( < \pm \frac<2><3><2>\normalsize>>> \right)^3> + C > = < \pm \frac<3> <2>\cdot \frac<8><<27>><2>\normalsize>> + C > = < \pm \frac<4><9><2>\normalsize>> + C.> \]

Это дифференциальное уравнение относится к случаю \(1,\) поскольку оно содержит переменную \(y\) и ее производную \(y’.\) Используя параметр \(p,\) мы можем переписать это уравнение в следующем виде: \[y = \ln \left( <25 +> \right).\] Возьмем дифференциалы от обеих частей: \[dy = \frac<<2pdp>><<25 +>>.\] Поскольку \(dy = pdx,\) то получаем: \[pdx = \frac<<2pdp>><<25 +>>,\;\; \Rightarrow dx = \frac<<2dp>><<25 +>>.\] Теперь можно проинтегрировать последнее выражение и найти \(x\) как функцию \(p.\) \[ ><<25 +>>> > = <2\int <\frac<><<25 +>>> > = <2 \cdot \frac<1><5>\arctan \frac

<5>+ C > = <\frac<2><5>\arctan \frac

<5>+ C.> \] В итоге мы получаем следующее параметрическое представление решения дифференциального уравнения: \[\left\< \begin x = \frac<2><5>\arctan \frac

<5>+ C\\ y = \ln \left( <25 +> \right) \end \right.,\] где \(C\) − произвольная постоянная.

Источник

2.4.1. Метод введения параметра

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-ГО ПОРЯДКА

2.3. Дифференциальные уравнения 1-го порядка, разрешенные относительно производной

2.4. Дифференциальные уравнения 1-го порядка, неразрешенные относительно производной

ГЛАВА 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

3.2. Случаи интегрирования ДУ высших порядков

ГЛАВА 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

4.3. Линейные неоднородные ДУ с постоянными коэффициентами (ЛНДУ)

5.1. Системы линейных однородных ДУ с постоянными коэффициентами

5.2. Системы линейных неоднородных ДУ с постоянными коэффициентами (СЛНДУ)

6.1. Простейшие типы точек покоя

7.1. Приближенно-аналитические методы решения задачи Коши

7.1.1. Методы степенных рядов

7.1.2. Метод последовательных приближений

7.2. Численные методы решения задачи Коши

7.4. Численные методы решения краевых задач

2.4. Дифференциальные уравнения 1-го порядка, неразрешенные относительно производной

ДУ 1-го порядка неразрешенное относительно производной характеризуется тем, что из него не может быть легко выражена производная .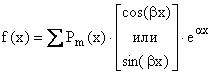

Одним из методов решения таких уравнений является применение математических преобразований, целью которых является выражение производной из ДУ. В результате получается одно или несколько ДУ вида:

Дано:

Выделим полный квадрат в левой и правой частях уравнения:

и

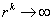
Получили два ДУ, разрешенных относительно производной:

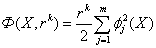
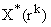
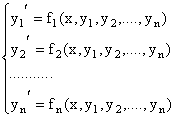
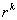
При интегрировании ДУ получаем , при интегрировании ДУ получаем .

Ответ: ,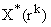

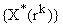
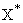
В общем случае алгоритмических методов решения ДУ, неразрешенных относительно производной, не существует, кроме случаев, когда из ДУ легко выражается или . В этом случае используют метод введения параметра.

2.4.1. Метод введения параметра

Из ДУ легко выражается :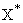

Из ДУ легко выражается :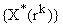

1. Разрешить ДУ относительно :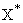

1. Разрешить ДУ относительно :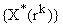

2. Ввести параметр 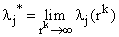, тогда получится:

3. Взять полный дифференциал правой и левой частей уравнения, получится:

4. Сделать замену в левой части ДУ:

, получится:

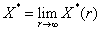
Это ДУ 1-го порядка, разрешенное относительно производной

Это ДУ 1-го порядка, разрешенное относительно производной

5. Решить полученное ДУ, записать его решение:

6. Записать решение исходного ДУ в параметрической форме:

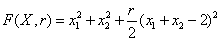
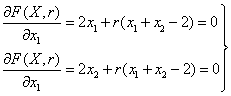
7. Проверить потерянные решения: все потерянные решения вида , подставляются в выражение из п. 2 алгоритма и принимают вид: или Затем следует проверка подстановкой в исходное ДУ

8. Записать общее решение ДУ

Дано:

1. Данное ДУ неразрешено относительно , но разрешено относительно :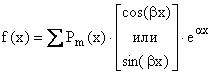

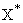
2. Введем параметр 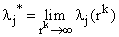, получим:

3. Возьмем полный дифференциал левой и правой части уравнения:

4. Сделаем замену 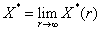, получим:

— получили ДУ с разделяющимися переменными

5. Решаем ДУ:

6. Запишем решение исходного ДУ в параметрической форме:

7. Проверяем возможно потерянные решения:

Подставляем в исходное ДУ:

8. Ответ:

В данном примере можно исключить параметр и получить решение в явном виде. Для этого выразим парметр из первого уравнения:

Затем подставим полученное выражение во второе уравнение: .

Ответ:

Источник

Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .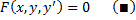

Уравнения первого порядка n-ой степени решаются так:

Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим , получим:

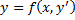
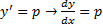
Продифференцируем по x:

Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: 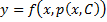. Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть . Вводим параметр , получаем . Дифференцируем по y обе части:

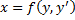
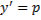
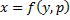
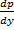
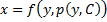
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: 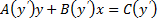. Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр 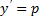, получаем:

Пусть 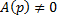, поделим всё выражение на A(p):

Продифференцируем по x:

Получили линейное уравнение первого порядка. Отсюда находим .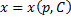

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :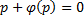

Если это тождество, то есть 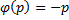, то:

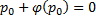
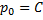
Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть , тогда – решение.

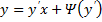
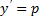
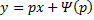
Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр , получаем . Дифференцируем по x, получаем:

Общее решение уравнения Клеро:

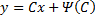
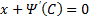
Здесь – семейство всевозможных кривых; – огибающая этого семейства, тоже является решением и называется особое решение.

Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.

Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой

Выражение для первой производной от y(x) не содержит производной от z(x):

.

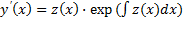
Поэтому, заменив в исходном уравнении y, y ‘. y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл.

Совокупность соотношений вида:

Где y1, y2, …, yn искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка.

Будем предполагать функции F2, F2, …, Fn такими, что система разрешима относительно производных от искомых функций:

Такие системы называются нормальными системами дифференциальных уравнений.

Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Семейство решений системы (2), зависящее от n произвольных постоянных C1, C2, …, Cn

называют обычно общим решением этой системы.

Дадим определение общего решения системы (2) в области D изменения переменных x, y1, y2, …, yn.

В качестве области D будем рассматривать область в пространстве (x, y1, y2, …, yn), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2).

Совокупность n функций (6), определённых в некоторой области изменения переменных x, C1, C2, …, Cn, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C1, C2, …, Cn в области D, так что при любых значениях x, y1, y2, …, yn, принадлежащих области D, системой (6) определяются значения C1, C2, …, Cn:

и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C1, C2, …, Cn, доставляемых формулами (7), когда точка (x, y1, y2, …, yn) пробегает область D.

Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C1, C2, …, Cn,, включая бесконечности, будет частным решением.

Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение.

1-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y1, …, yn любым частным решением этой системы она обращается в постоянную.

2-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), имеющая непрерывные частные производные по x, y2, …, yn, и такая, что в рассматриваемой области 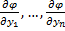не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:

.

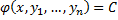
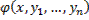
Равенство , где – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).

Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y1, y2, …, yn, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D.

Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ.

Система обыкновенных дифференциальных уравнений вида:

называется линейной системой. При система становится однородной. В векторно-матричной форме: , где
,

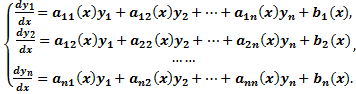
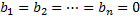
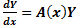
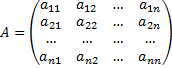
Будем искать решение . Ищем решение системы в таком виде:

Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций.

Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: .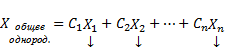

Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ.

Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка

Здесь A

Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ.

Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы 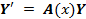, то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид:

где C — произвольный постоянный вектор-столбец, x0 — произвольная фиксированная точка из отрезка [a, b].

Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши.

Решением задачи Коши 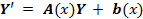, Y(x0) = Y0 является вектор-функция

Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ.

Определение системы неоднородных линейных ОДУ. Система ОДУ вида:

называется линейной неоднородной. Пусть

Система (*) в векторно-матричном виде: . — система однородная, иначе – неоднородная.

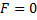
(произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x0, – любые.

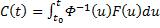
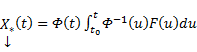
Видим, таким образом, что если в (3) в качестве C(t) брать , то вектор-функция будет решением системы (1).

Общее решение линейной неоднородной системы (1) может быть записано в виде . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию . Подстановка (4) начальных данных (5) даёт . Следовательно, решение задачи Коши (1)-(5) может быть записано в виде: . В частном случае, когда , последняя формула принимает вид: .

Источник