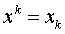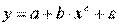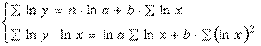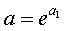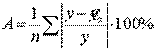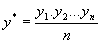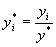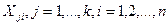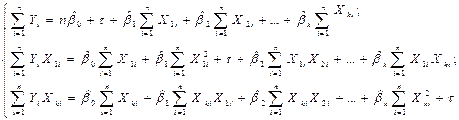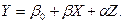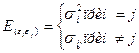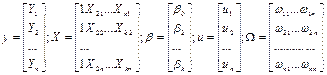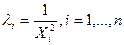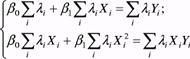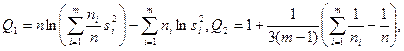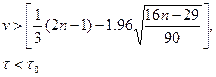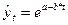Модели нелинейные по параметрам

Модели, нелинейные по параметрам

К нелинейным но параметрам моделям, оценка которых возможна методом линеаризации относятся следующие: степенная модель, показательная модель логистическая модель и некоторые мультипликативные комбинации из этих моделей.

Степенная модель

(9.10)

Степенные модели достаточно широко используются в экономике. К классу степенных функций относятся, в частности, модели спроса и предложения (кривые Эйнгеля), производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида продукции, а также зависимость валового национального дохода от уровня занятости.

Метод линеаризации степенных моделей заключается в логарифмировании обеих частей уравнения (9.10). Именно это послужило основанием к тому, чтобы случайное возмущение в модели записать не в виде слагаемого, а в виде сомножителя. Значение случайного возмущения в этом случае показывает долю случайного возмущения в значении эндогенной переменной.

В результате логарифмирования выражения (9.10) получим:

(9.11)

Далее делается замена переменных:

(9.12)

Подставив переменные (9.12) в (9.11) получим знакомое уравнение множественной линейной регрессии относительно новых переменных:

(9.13)

Для спецификации (9.13) формируется выборка наблюдений в соответствии с правилами и производится оценка и анализ модели. Чтобы получить модель в исходном виде (9.10) достаточно вычислить значение параметра и подставить оценки всех параметров в выражение (9.10).

Замечание. Остается открытым вопрос: по какому основанию логарифмировать уравнение (9.10)? В общем случае, по любому. На практике используют либо натуральное основание, либо десятичное.

Интерес представляет экономическая интерпретация параметров степенной модели. Рассмотрим для примера производственную функцию Кобба – Дугласа:

(9.14)

Вычислим производную функции (9.14) по фактору производства К:

Откуда следует, что

(9.15)

Выражение (9.15) представляет собой определение коэффициента эластичности переменной у по переменной х (в данном примере эластичность выпуска продукции по капиталу).

Таким образом, получили, что показатели степени при неременных в мультипликативной степенной модели являются соответствующими коэффициентами эластичности. Это важное свойство степенных моделей.

Остается вычислить оценки стандартных ошибок параметров и прогноза по модели степенного вида. Оценив модель (9.13), мы получим оценки стандартных ошибок параметров () и ошибку случайного возмущения. Опуская доказательства, отметим, что связь между оценками стандартных ошибок параметровии случайными возмущениями и инаходится исходя из приближенного равенства приращений и дифференциалов функций и для данной задачи эта связь имеет вид:

(9.16)

Пример. Оценим производственную функцию Кобба – Дугласа по данным табл. 9.2.

Источник

Виды нелинейных регрессионных моделей, расчет их параметров

Виды нелинейных регрессионных моделей, расчет их параметров

Оценка корреляции для нелинейной регрессии

Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так, близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.

В случае, когда между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.

Различают две группы нелинейных регрессионных моделей:

­- модели, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

К первой группе относятся, например, следующие виды функций:

Ко второй группе относятся:

Классическим примером функций, относящихся к первой группе, являются кривые Филипса и Энгеля:

и , соответственно.

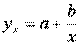
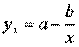
Первая функция характеризует нелинейные соотношения между нормой безработицы x и процентом прироста заработной платы у. Из данной зависимости следует, что с ростом уровня безработицы темпы роста заработной платы в пределе стремится к нулю.

Первая группа нелинейных функций легко может быть линеаризована (приведены к линейному виду). Например, для полинома к-го порядка

производя замену:

, , ,…,

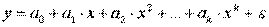
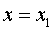
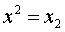
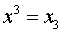
получим линейную модель вида

.

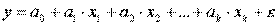
Аналогично могут быть линеаризованы и другие виды нелинейных функций 1-й группы, производя соответствующие замены.

Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций.

Иначе обстоит дело с группой регрессионных, нелинейных функций по оцениваемым параметрам. Данную группу функций можно разбить на две подгруппы: ­нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.

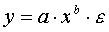
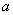
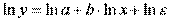
Рассмотрим степенную функцию . Она нелинейна относительно параметров и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:

.

Следовательно, ее параметры могут быть найдены обычным МНК.

Если модель представить в виде:

, то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.

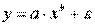
Внутренне нелинейной будет и модель вида

В эконометрических исследованиях, часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые легко преобразуются в линейный вид, относятся к группе линейных моделей. Например, к линейным относят модель:

, так как

.

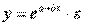
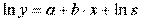
Если, модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные методы, успешность которых зависит от вида функции и особенностей применяемого итеративного подхода.

МНК в случае нелинейных функций, рассмотрим на примере оценки параметров степенной функции .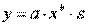

Прологарифмировав данную функцию, получим:

или, производя обозначения:

, где

; ; ; .

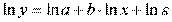
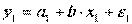
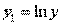
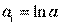
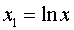
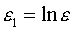
Применив МНК к полученному уравнению:

, или

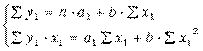
Параметр b определяется непосредственно из системы, а параметр а – косвенным путем:

Оценка корреляции для нелинейной регрессии

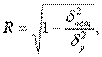
Оценка тесноты корреляционной зависимости в случае нелинейной регрессии производится с помощью индекса корреляции (R):

где ,, ,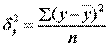

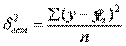
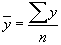
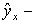
значения результативного признака, рассчитанные по уравнению регрессии.

Величина данного показателя находится в границах: 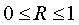, чем она ближе к единице, тем теснее связь рассматриваемых признаков, тем надежнее найденное уравнение регрессии.

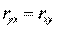
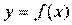
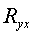
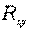
Следует помнить, что если для линейной зависимости имеет место равенство: , то при криволинейной зависимости не равен .Величина R 2 называется индексом детерминации.

Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:

,

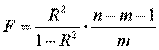
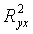
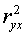
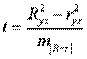
Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции.

,

где ,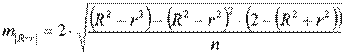

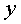
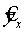
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

Существует и другая формула определения средней ошибки аппроксимации:

, где .

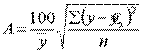
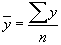
Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.

Возможность построения нелинейных моделей, как с помощью их приведения к линейному виду, так и путем использования нелинейной регрессии, значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя.

Если ограничиться парной регрессией, то можно построить график наблюдений у и х и принять решение. Однако очень часто несколько разных нелинейных функций приблизительно соответствуют наблюдениям, если они лежат на некоторой кривой. А в случае множественной регрессии невозможно даже построить график.

При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной процедура выбора достаточно проста. Наиболее разумным является оценивание регрессии на основе всех вероятных функций, и выбор функции, в наибольшей степени объясняющей изменения зависимой переменной. Если для одной модели коэффициент R 2 значительно больше, чем для другой, то вы сможете сделать оправданный выбор без особых раздумий, однако, если значения R 2 для двух моделей приблизительно равны, то проблема выбора существенно усложняется.

В этом случае следует использовать стандартную процедуру, известную под названием теста Бокса – Кокса.

Если необходимо сравнить модели с использованием у и lny в качестве зависимой переменной, то можно использовать вариант теста, разработанный Полом Зарембкой. Процедура включает следующие шаги:

1) Вычисляется среднее геометрическое значений у в выборке, (оно совпадает с экспонентой среднего арифметического lny):

2) Пересчитываются наблюдения у, т.е. они делятся на это значение, то есть

3) Оценивается регрессия для линейной модели с использованием у * _i вместе y_i и для логарифмической модели с использованием ln(y * _i) вместо ln(y_i). Теперь значения суммы квадратов отклонений для двух регрессий сравнимы, и, следовательно, модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.

Список рекомендуемой литературы:/1, 2, 6, 8, 9/

Мультиколлинеарность

1. Мультиколлинеарность, ее виды

2. Методы устранения мультиколлинеарности

3. Фиктивные переменные

Мультиколлинеарность, ее виды

Наиболее широко используются для решения вопроса об отборе факторов частные коэффициенты корреляции, оценивающие в чистом виде тесноту связи между фактором и результатом.

При включении факторов следует придерживаться правила, согласно которому число включаемых в модель объясняющих переменных должно быть в 5-6 раз меньше объема совокупности, по которой строится регрессия. Иначе число степеней свободы остаточной вариации будет мало, и параметры уравнения регрессии окажутся статистически незначимы.

Иногда при отборе переменных-факторов нарушается предположение (3.5). В этом случае говорят, что объясняющие переменные X _jt, j = l. k,i = 1,2. n модели характеризуются свойством полной (строгой) мультиколли­неарности. В этом случае система (3.6) не может быть разрешена относительно неизвестных оценок коэффициентов. Строгая мультиколлинеарность встреча­ется редко, так как ее несложно избежать на предварительной стадии отбора объясняющих переменных.

Реальная (частичная) мультиколлинеарность возникает в случаях доста­точно сильных линейных статистических связей между переменными

Точных количественных критериев для проверки наличия мультиколлинеарности не существует, но имеются некоторые практические ре­комендации по выявлению мультиколлинеарности.

1) Если среди парных коэффициентов корреляции между объясняющими переменными имеются значения 0,75-0,80 и выше, это свидетельствует о при­сутствии мультиколлинеарности.

2) О присутствии явления мультиколлинеарности сигнализируют некото­рые внешние признаки построенной модели, являющиеся его следствиями:

— некоторые из оценок 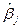, j=l,2. k имеют неправильные с точки зрения экономической теории знаки или неоправданно большие по абсолютной вели­чине значения,

— небольшое изменение исходной выборки (добавление или изъятие ма­лой порции данных) приводит к существенному изменению оценок коэффици­ентов модели вплоть до изменения их знаков,

— большинство оценок коэффициентов регрессии оказываются статисти­чески незначимо отличающимися от нуля, в то время как в действительности многие из них имеют отличные от нуля значения, а модель в целом является значимой при проверке с помощью F-критерия.

Методы устранения мультиколлинеарности

1) Проще всего удалить из модели один или несколько факторов.

2) Другой путь состоит в преобразовании факторов, при котором умень­шается корреляция между ними. Например, при построении регрессий на осно­ве динамических рядов помогает переход от первоначальных данных к первым разностям .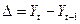

3) Использование в уравнении регрессии взаимодействия факторов, на­пример, в виде их произведения.

4) Использование так называемой ридж-регрессии (гребневой регрессии).
В этом случае к диагональным элементам системы добавляется «гребень» τ (небольшое число, как правило, от 0,1 до 0,4):

Это делает получаемые оценки смещенными, но уменьшает средние квадраты ошибок коэффициентов.

5) Использование метода главных компонент.

6) Отбор наиболее существенных объясняющих переменных на основе методов исключения, включения, шаговой регрессии, которые используют для принятия решения F-критерий.

Фиктивные переменные

Факторы (объясняющие переменные), применяемые в задаче регрессии до сих пор, принимали значения из некоторого непрерывного интервала. Ино­гда может понадобиться ввести в модель переменные, значения которых детер­минированы и дискретны. Например, данные получены для трех разных рай­онов, или на двух фабриках, или на разных машинах и т.п. Переменные такого типа обычно называют фиктивными или искусственными. Эти переменные по­зволяют отразить в модели эффекты сдвига во времени или в пространстве, воздействия качественных переменных.

Например, необходимо отразить в модели разное происхождение куриных окорочков, часть из которых полу­чены в Америке, а часть в Канаде, при построении регрессионной зависимости веса окорочков Y от возраста кур X. Для этого в модель включим фиктивную переменную Z: Z = 0 для Америки, Z = l для Канады:

Ясно, что для какой-либо задачи существует не единственный способ вы­бора фиктивных переменных, а в большинстве случаев путей их представления много. Это обстоятельство оказывается выгодным, поскольку в некоторых слу­чаях можно угодить в ловушку, когда существует линейная зависимость между введенными фиктивными переменными.

Пример. Предположим, что исследуется зависимость между весом ново­рожденного и семейным положением матери, а также рожала ли она раньше.

При этом двойном наборе фиктивных переменных имеется четыре воз­можных случая с соответствующими комбинациями значений фиктивных пе­ременных:

1) Замужняя мать, первые роды М = 0, D = 0.

2) Одинокая мать, первые роды M = l, D = 0.

3) Замужняя мать, не первые роды М = 0, D = 1.

4) Одинокая мать, не первые роды M = l, D = 1

Первый случай по смыслу является основной совместной эталонной­ категорией. Коэффициент при М будет представлять оценку разности веса новорожденных, если мать одинока (ожидаем отрицательный знак коэффициента). Коэффициент при D будет представлять оценку дополнительного веса при рожде­нии, если ребенок не является первенцем. Ребенок для четвертой категории ма­терей будет подвержен обоим воздействиям.

Фиктивные переменные могут быть введены не только в правую часть регрессионного соотношения, но и зависимая переменная может быть представлена в такой форме. Это возможно в тех случаях, когда в качестве зависи­мой переменной мы рассматриваем ответы на вопросы, пользуется ли человек собственной машиной, имеет ли счет в банке и т.п., причем во всех случаях за­висимая переменная принимает дискретные значения.

Фиктивные переменные могут быть использованы для учета взаимодействия между различными группами факторов.

Такой подход позволяет проверить различные варианты гипотез:

1) Гипотеза Н₀: 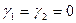против альтернативы Hi: что это не так. Если
гипотеза Н₀ будет отвергнута, то мы придем к выводу, что модели не одинаковы, а если нет, то можно пользоваться одной моделью независимо от происхо­ждения окороков.

2) Если гипотеза Н₀ в предыдущем пункте будет отвергнута, то можно
проверить гипотезу Но: γ₂=Q. Если Н₀ принимается, то мы заключаем, что имеющиеся два набора данных отличаются только уровнем, имея одинаковые углы наклона.

При необходимости могут быть выбраны и другие варианты проверок, если это разумно для задачи.

Как показывает пример, использование взаимодействия с фиктивными переменными упрощает построение подходящих критериев и получение пра­вильных статистик для проверки гипотез.

Список рекомендуемой литературы: /1, 2, 3, 5, 8, 9/

Гетероскедастичность

1. Обобщенный метод наименьших квадратов

2. Линейная модель множественной регрессии с гетероскедастичными остатками

3. Способы проверки выборки на гомоскедастичность

Обобщенный метод наименьших квадратов

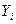
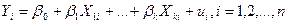
Обобщим КЛММР вида (5.1). Пусть по-прежнему мы располагаем выбо­рочными наблюдениями над k переменными и X _jn j=l. k, г’=1,2. n и строим регрессию:

(10.1)

Откажемся от предположения КЛММР о некоррелированности и гомоскедастичности случайной ошибки (5.3). То есть относительно переменных мо­дели в уравнении (10.1) примем следующие основные гипотезы:

(10.2)

(10.3)

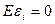
Не должно существовать строгой линейной зависимости между переменными Xi, Х₃. Хk. (10.5)

Модель вида (10.1)-(10.5) называется обобщенной линейной моделью мно­жественной регрессии (ОЛММР). Отличие ОЛММР от КЛММР состоит в из­менении предположений о поведении случайной ошибки (10.3).

К ОЛММР может быть применен метод наименьших квадратов, однако он оказывается неприменимым к модели (10.1)-(10.5) в силу потери свойства оптимальности оценок. Но МНК к ОЛММР может быть применен.

Обозначим:

Тогда модель (10.1)-(10.5) запишется в матричном виде:

y = xβ + u, при условиях

i ₌1, 2. n,
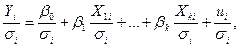
и получим регрессию с постоянной (гомоскедастичной) дисперсией случайного члена, действительно V

Для получения оценок неизвестных дисперсий 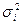, i=l. n будем пред­полагать, что они пропорциональны некоторым числам, т.е.

Принимая различные гипотезы относительно характера гетероскедастичности, будем иметь соответствующие значения .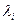

Если дисперсия случайного члена пропорциональна квадрату регрессора X, так что Е(иi 2 ) =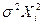, i =1,n, то

Например, для случая одной объясняющей переменной имеем в этом случае систему уравнений ОМНК вида:

Поскольку значения 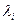, i =1. n являются фактически весами, которые устраняют неоднородность дисперсии, то ОМНК для системы с гетероскедастичностью часто называют методом взвешенных наименьших квадратов.

Существуют также и другие методы коррекции модели на гетероскедастичность, в частности состоятельное оценивание стандартных ошибок. Из­вестны способы коррекции стандартных ошибок Уайта и Невье-Веста.

10.3 Способы проверки выборки на гомоскедастичность.

Рассмотрим вопрос тестирования выборки на наличие гомоскедастичности. Возможности такой проверки зависят от природы исходных данных.

Если имеется обширная выборка, то можно воспользоваться стандартным критерием однородности дисперсии Бартлетта.

Расчленяя выборку на т независимых групп (каждой из них соответству­ет единственное значение переменной X), вычислим величины:

В случаях малого количества наблюдений в выборке, когда группировка данных невозможна, используется тест Голдфелда и Куандта.

Он предусматри­вает осуществление следующих шагов:

1) Упорядочить наблюдения по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.

2) Опустить v наблюдений, оказавшихся в центре (v должно быть при­мерно равно четверти общего количества наблюдений n).

Если хотя бы одно из неравенств:

окажется нарушенным, то гипотеза Н₀ отвергается с вероятностью ошибки а, заключенной между 0,05 и 0,0975. Величина Т₀ определяется в зависимости от n:

— экспоненциальная:

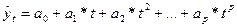
— полиномы второго и более высоких порядков:

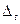
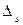
Выбор функции тренда может быть осуществлен несколькими способами. Наиболее простым считается тот, в ходе которого анализируют цепные аб­солютные приросты (первые разности уровней ряда) , абсолютные ускорения уровней ряда (вторые разности ряда) и цепные коэффициенты ростам,.

Если примерно одинаковы 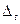, то ряд имеет линейный тренд, если же примерно постоянны , то для описания тенденции временного ряда следует выбрать параболу второго порядка, и, если примерно равны K_t, необходимо использовать экспоненциальную или степенную функции.

Трактовка параметров степенного тренда аналогична трактовке параметров экспоненциального тренда.

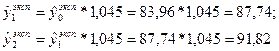Метод последовательных разностей

Часто при аналитическом выравнивании ряда используется модель тренда в виде полинома.

Для определения порядка аппроксимирующего полинома в этом случае выделения тренда широко используется метод последовательных разностей,членов анализируемого временного ряда.

Аддитивная и мультипликативная модели временного ряда

Простейшим подходом к моделированию динамических рядов, содержащих сезонные колебания, является построение аддитивной или мультипликативной моделей временного ряда.

Выбор одной из этих моделей основывается на анализе структуры временного ряда.

Если амплитуда сезонных колебаний примерно постоянна, то строят аддитивную модель. Если же амплитуда колебаний непостоянна, то есть возрас­тает или уменьшается, то строят мультипликативную модель.

Процесс построения модели ряда в этом случае включает следующие этапы:

1) Выравнивание исходного ряда методом скользящей средней. Расчет значений сезонной компоненты S.

5) Расчет абсолютных и/или относительных ошибок.

Рассмотрим процесс построения аддитивной модели на примере.
Модели стационарных и нестационарных динамических рядов и их идентификация

Модели авторегрессии порядка р (AutoRegressive — AR(p) models)

Достаточно часто экономические показатели, представленные в виде временного ряда, имеют сложную структуру. Моделирование таких рядов путем построения модели тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам. Ряд остатков часто имеет статистические закономерности. Наиболее распространенными моделями стацио­нарных рядов являются модели авторегрессии и модели скользящего среднего.

Будем рассматривать класс стационарных динамических рядов. Задача со­стоит в построении модели остатков временного ряда и, и прогнозирования его значений.

Авторегрессионная модель предназначена для описания стационарных динамических рядов. Стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка с достаточно быстро убывающими коэффициентами. В частности, поэтому авторегрессионная модель достаточно высокого по­рядка может хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель авторегрессии часто применяется для моделирования ос­татков в той или иной параметрической модели, например регрессионной мо­дели или модели тренда.

Список рекомендуемой литературы: /2, 4, 5, 9/

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. Елисеева И.И. Эконометрика. – М.: Финансы и статистика. 2000.

2. Елисеева И.И. Практикум по эконометрике. – М.: Финансы и Статистика. 2001.

3. Карасев А.И., Кремер Н.Ш., Математические методы и методы планирования. – М.: Экономика, 1987.

4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2003. – 311 с.

5. Кулиныч Е.И. Эконометрия – М.: Финансы и статистика, 2000.

6. Магнус Я.Р. и другие Эконометрика. Начальный курс. – М.: Дело, 2000.

8. Четыркин Е.М. Статистические методы прогнозирования. М.: Финансы и статистика, 1979.

Дополнительная литература

1. Айвазян С.А., и другие Прикладная статистика. Исследование зависимостей. – М: Финансы и статистика, 1985.

3. Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001.

4. Горчаков А.А., и другие Методы экономико – математического моделирования и прогнозирования в новых условиях хозяйствования. – М: ВЗФЭИ, 1991.

Источник