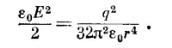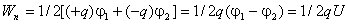момент сил действующих на диполь во внешнем электрическом поле

Электрический диполь. Момент сил, действующий на диполь. Энергия диполя в поле

Электрическим диполем называется система двух равных по модулю разноименных точечных зарядов (+q, — q), находящихся на конечном расстоянии / другуг друга.

Плечо диполя / — вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними.

Электрический момент диполя р — вектор, совпадающий по направлению с плечом диполя, направленный от отрицательного заряда к положительному и равный произведению модуля заряда q на плечо / :

Рис. 12.12. К вычислению потенциала поля диполя

Согласно формуле для потенциала точечного заряда (12.19), потенциал электростатического поля диполя в точке А (рис. 12.12) определяется так:

Найдем по формуле (12.24) проекции вектора Ё:

где направление 1_< совпадает с направлением радиус-вектора г, а другое направление /₂ лежит в плоскости с осью диполя и направлено перпендикулярно к г в сторону возрастания угла 9 (рис. 12.13). При этом d^—dr, dl₂ = rdQ.

Рис. 12.13. К вычислению электрического поля диполя

Отсюда получаем, что модуль вектора Е поля диполя в точке А определяется как

Можно доказать, что действующая на диполь сила

где —— — производная вектора Е по направлению, совпадающему с век- 01

— = 0 и F — 0. Значит, сила действует на диполь только в неоднородном

Момент сил, действующий на диполь. Во внешнем электрическом поле на заряды диполя действует пара сил, которая стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля Ё.

Во внешнем однородном поле (рис. 12.14, а), согласно определению (см. формулу (4.42)), момент пары сил

Хотя создается вращающий момент, результирующая пары сил равна нулю и диполь в поле не перемещается. Момент сил стремится развернуть диполь вдоль силовой линии электрического поля. Вектор М направлен перпендикулярно р и Ё по правилу векторного произведения.

Рис. 12.14. Диполь во внешнем электростатическом поле: а — в однородном; б — в неоднородном

Во внешнем неоднородном поле (рис. 12.14, б) силы, действующие на концы диполя, неодинаковы (|/₂| > |/j|). Их результирующая сила стремится передвинуть диполь. Диполь втягивается в область поля с большей

Энергия диполя в поле. По формуле (12.17) энергия точечного заряда во внешнем поле W — qq>, где ф — потенциал поля в точке нахождения заряда q. Поэтому энергия диполя во внешнем поле

где ф₊ и ф_ — потенциалы внешнего поля в точках расположения зарядов q₊ и q_ соответственно. С точностью до величины второго порядка малости, учитывая выражение (12.26), получаем

где — — производная потенциала по направлению вектора /. Поэтому д!

Следовательно, минимальную энергию (Ж_мин = — рЕ) диполь имеет в положении устойчивого равновесия, когда направления векторов р и Е совпадают между собой. При отклонении из этого положения возникает момент внешних сил, возвращающих диполь к положению равновесия.

Источник

Электрический диполь. Электрический момент диполя. Момент сил, действующих на диполь во внешнем электрическом поле

Энергия системы точечных зарядов. Энергия заряженного проводника.

даже у отдельного точечного заряда q имеется какая-то электростатическая энергия. Поле в этом случае дается выражением так что плотность энергии на расстоянии r от заряда равна

Энергию заряженного конденсатора можно представить в виде

Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.

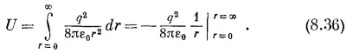
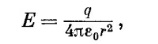
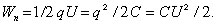
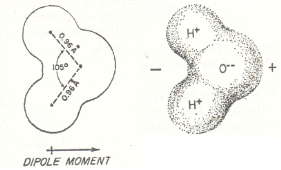
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга.

Слева силовые линии диполя, справа — пример диполя (молекула воды).

Дипольный момент — векторная физическая величина, характеризующая электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей.

Простейшая система зарядов, имеющая ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда н а расстояние между зарядами и направлен от отрицательного заряда к положительному, или:

, где — величина положительного заряда, — вектор с началом в отрицательном заряде и концом в положительном.

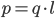
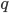
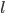
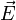
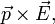
Во внешнем электрическом поле на электрический диполь действует момент сил который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.

Диэлектрики и их классификация. Определение вектора поляризации и диэлектрической восприимчивости. Поляризация полярных и неполярных диэлектриков.

Диэлектрик (изолятор) — вещество, плохо проводящее электрический ток.

Основное свойство диэлектрика — способность поляризоваться во внешнем электрическом поле.

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей под воздействием внешнего электрического поля, других внешних сил или спонтанно.

Поляризацию диэлектриков характеризует вектор поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации называют просто поляризацией.

Диэлектрическая восприимчивость(поляризуемость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость χ_ε — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:

, где ε₀ — электрическая постоянная; произведение ε₀χ_ε называется абсолютной диэлектрической восприимчивостью.

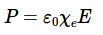
В случае вакуума χ_ε = 0.

У диэлектриков, как правило, она положительна. Диэлектрическая восприимчивость измеряется в ничём (безразмерная величина).

Ряд диэлектриков проявляют особые физические свойства. К ним относятся пьезоэлектрики (которые могут либо под действием деформации индуцировать электрический заряд на своей поверхности, или наоборот), пироэлектрики (поляризация в отсутствие внешних воздействий), сегнетоэлектрики (обладающие в определённом интервале температур собственным дипольным моментом), и.т.д.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Момент сил, действующий на диполь во внешнем электрическом поле

Поместим диполь в электрическое поле (рис. 17.4). Пусть направление диполя составляет с направлением вектора напряженности некоторый угол . На отрицательный заряд действует сила , направленная против поля, на положительный заряд действует сила , направленная вдоль поля.
Рис. 17.4

Эти силы образуют пару сил с вращающим моментом:

.

Диполь в однородном внешнем поле поворачивается под действием вращающего момента таким образом, чтобы сила, действующая на положительный заряд диполя, совпадала по направлению с вектором и осью диполя. Этому положению соответствует и

Энергия диполя в электрическом поле
Имеется в виду потенциальная энергия диполя в однородном электрическом поле, которая, если диполь «отпустить», произведёт работу, поворачивая диполь. Работа при вращательном движении соответствует убыли потенциальной энергии диполя:

Отсюда потенциальная энергия диполя:

· максимальна (рЕ), когда антипараллельны,

· равна нулю, когда перпендикулярны.

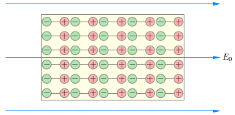
14. Полярные и неполярные диэлектрики.Все диэлектрики делятся на две категории. Диэлектрики, относящиеся к первой категории, имеют молекулы, которые даже в отсутствии внешнего электрического поля образуют диполи. Они называются полярными. К полярным диэлектрикам относятся вода аммиак ацетон и эфир. Диполи таких диэлектриков в отсутствии поля расположены хаотически вследствие теплового движения. И, следовательно, заряд на поверхности такого вещества равен нулю.

Но при внесении его во внешнее электрическое поля диполи то есть молекула стремятся развернуться вдоль поля. Получается, что положительный заряд предыдущего диполя смотрит на отрицательный следующего. Следовательно, они компенсируют друг друга. Но вот диполям находящимся возле самой поверхности не находится пара. Таким образом, на поверхности материала образуются нескомпенсированые связанные заряды. С одной стороны положительные с другой отрицательные. Но этому препятствует тепловое движение молекул.

Рисунок 1 — поляризация полярного диэлектрика

Вторая категория диэлектриков это те, у которых внутри молекулы в свободном состоянии есть положительный и отрицательный заряды. Но они находятся так близко друг к другу, что их влияние взаимно компенсируется. Но при внесении такой молекулы в поле заряды сместятся на некоторое расстояние. Таким образом, образуется диполь. На такие молекулы не влияет тепловое движение и, следовательно, поляризация в них не зависит от температуры.

Рисунок 2 — поляризация неполярного диэлектрика

15. Связанные и сторонние заряды.

16. Электрическое поле в диэлектрике.

18. Поляризованность P:

20. Зависимость поляризованности от температуры и частоты внешнего поля.

В слабых полях:

В сильных полях: В достаточно сильных полях всё описанное выше осложняется тем, что по мере роста напряженности электрического поля рано или поздно теряется линейность зависимости P от E.

22. Интегральная форма теоремы Гаусса:

дифференциальная форма теоремы Гаусса:

23. Физический смысл коэффициента относительной диэлектрической проницаемости:Это безразмерная физическая величина, характеризующая свойства изолирующей среды. Она показывает, во сколько раз взаимодействие между зарядами в однородной среде меньше, чем в ваакуме.

24. Граничные условия для векторов E и D: Для касательных составляющих вектора электрической индукции граничное условие имеет вид

Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора непрерывна, а касательная составляющая вектора терпит разрыв.

25. Проводник в электрическом поле: 1)Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Значит, напряженность поля во всех точках внутри проводника равна нулю:

2)Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е.поверхность проводника в электростатическом поле является эквипотенциальной.

3) Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместяться только на поверхности проводника.

26. Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля.

27. Уравнение Пуассона.В трёхмерной декартовой системе координат уравнение принимает форму:

В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

и будет равен нулю во всех точках, для которых

Если мы помещаем q` на расстоянии а 2 /b от центра, то отношение r₂/r₁ равно постоянной величине alb. Тогда если

то сфера станет эквипотенциалью. Потенциал ее на самом деле будет равен нулю.

30. Электроемкость проводника. Электроемкость шара.

31. Конденсатор:двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Электроемкость конденсатора:

Электроемкости плоского конденсатора:

(сферический конденсатор),
(цилиндрический конденсатор).

Параллельное соединение конденсаторов:

Емкость последовательно соединенных конденсаторов:

32. Энергия взаимодействия системы электрических зарядов:

Энергия системы заряженных проводников:
Энергия конденсатора:

Энергия электрического поля и в диэлектрике:

Плотность энергии электрического поля:

33. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля.

35. Принцип суперпозиции:один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

36. Закон био-савара-лапласа:

37. Применение законабио-савара-лапласа для расчета магнитных полей:

38. Магнитное поле прямого тока:

39. Магнитное поле на оси кругового тока: .

40. Теорема гаусса для поля B: — дифференциальный вид.

-интегральный.

41. Теорема о циркуляции вектора магнитной индукции в интегральной форме:

— в дифференциальной.

42.Применение т. О циркуляции B: поле бесконечно прямого проводника с током

Поле соленоида

Поле тороида:

Поле с током:

42. Сила Ампера:

43. Работа по перемещению проводника с током в магнитном поле:

44. Магнитный потокΦ =B·S· cos α

на контуре максимален:Φ_max=B·S

45. Момент сил действующих на контур с током в магнитном поле: ,

Источник