на гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

На гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

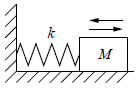
На гладком горизонтальном столе брусок массой М, прикреплённый к вертикальной стене пружиной жёсткостью k, совершает гармонические колебания с амплитудой А (см. рисунок). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) период колебаний груза

Б) амплитуда скорости груза

1)

2)

3)

4)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Период колебаний пружинного маятника равна (А — 1).

Максимальная потенциальная энергия пружины равна максимальной кинетической энергии Из равенства следует, что амплитуда скорости груза равна (Б — 4).

Источник

На гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

На гладком горизонтальном столе брусок массой М, прикреплённый к вертикальной стене пружиной жёсткостью k, совершает гармонические колебания с амплитудой А (см. рисунок). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) период колебаний груза

Б) амплитуда скорости груза

Колебательным называется любое периодически повторяющееся движение. Оно описывается гармоническими функциями, такими как [math]\sin,\cos[/math]. Зависимость координаты тела от времени имеет вид [math]\mathrm x(\mathrm t)=\mathrm(\mathrm<ωt>+<\mathrm\varphi>_0)[/math], где A- амплитуда колебания [math]\mathrm\omega[/math], некоторое число (зависящая от параметров колебательной системы, [math]\varphi_0[/math] начальная фаза колебания. Период колебания связан с циклической частотой следующим образом [math]\mathrm T=\frac<2\mathrm\pi><\mathrm\omega>[/math].

для пружинного маятника [math]\mathrm\omega=\sqrt<\frac<\mathrm k><\mathrm m>>[/math]

Амплитуду колебаний можно найти по закону сохранения энергии. В точке максимального отклонения энергия системы равна максимальной потенциальной энергии системы и равна [math]\frac<\mathrm^2>2[/math]

В положении равновесия потенциальная энергия системы равна нулю а кинетическая максимальна и равна [math]\frac<\mathrm m\mathrm v^2>2[/math]

Приравнивая эти 2 величины можно найти чему равна скорость v

Ответ: 14
2 1 6 5 6 5 0

Источник

На гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

На гладком горизонтальном столе брусок массой М, прикреплённый к вертикальной стене пружиной жёсткостью k, совершает гармонические колебания с амплитудой А (см. рисунок). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

А) период колебаний груза

Б) амплитуда скорости груза

1)

2)

3)

4)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Период колебаний пружинного маятника равна (А — 1).

Максимальная потенциальная энергия пружины равна максимальной кинетической энергии Из равенства следует, что амплитуда скорости груза равна (Б — 4).

Источник

На гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

Тела 1 и 2 находятся на гладкой горизонтальной плоскости (см. рисунок, вид сверху). На них одновременно начинают действовать постоянные силы, равные, соответственно, F₁ = 3 Н и F₂. Чему равно изменение проекции импульса системы этих тел на ось OX за первые две секунды? (Ответ дайте в килограммах на метр в секунду.)

Согласно второму закону Ньютона, сила есть отношение изменения импульса к промежутку времени, за которое произошло это изменение:

Проекция силы на ось OX равна 3 Н, а значит

Проекция силы на ось OX равна –3 Н, а значит

Следовательно, изменение проекции импульса системы этих тел на ось OX равно 0.

Маленький шарик массой подвешен на лёгкой нерастяжимой нити длиной которая разрывается при силе натяжения Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго сталкивается с бруском массой лежащим неподвижно на гладкой горизонтальной поверхности стола. Какова скорость u бруска после удара? Считать, что брусок после удара движется поступательно.

1. Непосредственно перед обрывом нити в момент прохождения положения равновесия шарик движется по окружности радиусом l со скоростью В этот момент действующие на шарик сила тяжести и сила натяжения нити направлены по вертикали и вызывают центростремительное ускорение шарика (см. рисунок). Запишем второй закон Ньютона в проекциях на ось Oy инерциальной системы отсчёта Oxy, связанной с Землёй:

откуда

2. При прохождении положения равновесия нить обрывается, и шарик, движущийся горизонтально со скоростью абсолютно неупруго сталкивается с покоящимся бруском. При столкновении сохраняется импульс системы шарик — брусок. В проекциях на ось Ox получаем:

где u — проекция скорости бруска с шариком после удара на эту ось. Отсюда:

Ответ:

На покоящееся точечное тело массой 0,5 кг, находящееся на гладкой горизонтальной поверхности, в момент времени t₀ = 0 начинает действовать сила, всегда направленная горизонтально вдоль одной прямой. График зависимости проекции F этой силы на указанную прямую от времени t изображён на рисунке.

Выберите все верные утверждения на основании анализа представленного графика.

1) В момент времени t = 3 с модуль скорости тела равен 16 м/с.

2) Изменение модуля импульса тела за третью секунду меньше, чем за четвёртую секунду.

3) В момент времени t = 8 с импульс тела равен 0 кг·м/с.

4) Модуль скорости тела в конце первой секунды больше модуля скорости тела в конце десятой секунды.

5) Изменение кинетической энергии тела за первую секунду меньше, чем за девятую секунду.

1) К моменту времени t = 3 с тело на протяжении двух секунд получало ускорение Следовательно, его скорость равна 16 м/с. Первое утверждение верно.

2) Со второй по четвёртую секунду на тело не действовала никакая сила. Поэтому изменение модуля импульса и за третью и за четвёртую секунду равно нулю. Второе утверждение неверно.

3) Найдём импульс тела к моменту времени t = 8 с. Изменение импульса тела равно сумме импульсов сил, действовавших на тело. Импульс тела в начальный момент равен нулю, следовательно, импульс тела к восьмой секунде равен: Третье утверждение верно.

4) Ускорение тела в промежутке времени от начала движения до 2 секунды равно Значит, скорость приобретённая за это время равна А модуль скорости тела в конце первой секунды равен Ускорение тела в промежутке времени от 2 до 4 с равно нулю. Ускорение тела в промежутке времени от 4 до 10 с равно Следовательно, проекция скорости тела в конце десятой секунды будет равна Таким образом, модуль скорости тела в конце первой секунды равен модулю скорости тела в конце десятой секунды. Четвёртое утверждение неверно.

5) Как было посчитано в п. 4 скорость в конце первой секунды равна 8 м/с. Изменение кинетической энергии за первую секунду равно В начале девятой секунды проекция скорости равна в конце девятой секунды — Изменение кинетической энергии равно Таким образом, изменение кинетической энергии тела за первую секунду больше, чем за девятую секунду. Пятое утверждение неверно.

Источник

На гладком горизонтальном столе брусок массой м прикрепленный к вертикальной стене пружиной

На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рисунок). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.

Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.

Обоснование. Трубка находится на гладком столе, т.е. отсутствует сил трения. Поверхность трубки гладкая, следовательно, на шарик не действует сила трения. В инерциальной системе отсчета при взаимодействии трубки и шарика можно применять закон сохранения импульса. Внешние силы тяжести и реакции опоры можем не учитывать при рассмотрении изменения скорости тел в горизонтальном направлении. По тем же причинам система «трубка-шарик» является замкнутой, поэтому в инерциальной системе отсчета применим закон сохранения энергии.

Перейдем к решению.

1. Из условия задачи следует, что шарик вылетит из трубки с некоторой скоростью относительно стола, а брусок приобретёт горизонтальную скорость направленную влево (см. рисунок).

2. Поскольку шарик в системе отсчёта, связанной с бруском, вылетает вдоль трубки со скоростью направленной под углом к горизонту, а сама трубка в момент вылета шарика движется влево со скоростью согласно классическому закону сложения скоростей имеем: и и по теореме косинусов

3. Поскольку механическая энергия системы сохраняется, то можно записать:

4. Сохраняется также и нулевая горизонтальная проекция импульса системы, так что

5. Решая полученную систему уравнений, находим модуль искомой скорости бруска:

м/с.

Ответ: м/с.

Источник