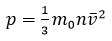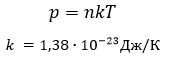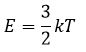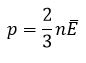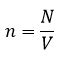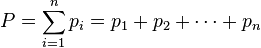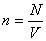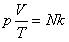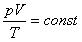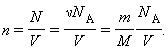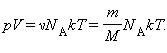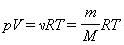Назовите макроскопические параметры газа

Макроскопические параметры. Идеальный газ.

Состояние газа (так же как жидкости и твердого тела) может быть описано и без рассмотрения молекулярного строения вещества. Это делают с помощью макроскопических величин, совокупность которых однозначно определяет состояние системы. Такие величины называют параметрами состояния (или термоди­намическими параметрами). Параметрами состояния любой системы являются ее объем, давление и температура. Если в каком-либо процессе изменяется хотя бы один из параметров состояния системы, то и само состояние системы становится другим.

Величины, характеризующие состояние макроскопических тел без учета их внутреннего строения называются макроскопическими параметрами.

Идеальный газ – это модель реального газа, которая обладает следующими свойствами:

1. Молекулы пренебрежимо малы по сравнению со средним расстоянием между ними.

2. Молекулы ведут себя подобно маленьким твердым шарикам: они упруго сталкиваются между собой и со стенками сосуда, никаких других взаимодействий между ними нет.

3. Молекулы находятся в непрекращающемся хаотическом движении.

Все газы при не слишком высоких давлениях и при не слишком низких температурах близки по своим свойствам к идеальному газу. При высоких давлениях молекулы газа настолько сближа­ются, что пренебрегать их собственными размерами нельзя. При понижении температуры кинетическая энергия молекул уменьшается и становится сравнимой с их потенциальной энер­гией, следовательно, при низких температурах пренебрегать по­тенциальной энергией нельзя.

При высоких давлениях и низких темпера­турах газ не может считаться идеальным. Такой газ называют реальным. (Поведение реального газа описывается законами, отличающимися от законов идеального газа.)

2. Давление газа. Основное уравнение МКТ газа.

Давление газа определяется столкновением молекул газа со стенками сосуда.

В СИ за единицу давления принимают 1 Па.

Давление, при котором на площадь 1 м 2 действует сила давления в 1 Н, называется Паскалем.

Одной из основных задач молекулярно-кинетической теории газа является установление количественных соотношений между макроскопическими параметрами, характеризующими состояние газа (давлением, температурой), и величинами, характеризую­щими хаотическое тепловое движение молекул газа (скоростью молекул, их кинетической энергией). Одним из таких соотноше­ний является зависимость между давлением идеального газа и средней кинетической энергией поступательного движения его молекул. Эту зависимость называют основным уравнением моле­кулярно-кинетической теории идеального газа:

или

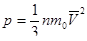
где р — давление газа; n — концентрация молекул газа (число его молекул в единичном объеме): m₀ — масса молекулы газа, — средняя квадратичная скорость движения газовых молекул; —средняя квадратичная энергия поступатель­ного движения молекул идеального газа.

Давление идеального газа пропорционально средней кинетической энергии поступательного движения молекул и концентрации молекул.

Это давление тем больше, чем больше средняя кинетическая энергия поступательного движения молекул.

Средней квадратической скоростью называют величину, рав­ную корню квадратному из среднего арифметического значения квадратов скоростей N молекул газа:

Средней кинетической энергией поступательного движения молекул идеального газа называют величину

С учетом основного уравнения МКТ имеем:

Из этой формулы видно, что средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре.

Давление газа зависит от концентрации молекул. Эта зависимость выражается формулой:

Давление газа не зависит от его природы, а определяется только концентрацией молекул и температурой газа.

Численное значение средней квадратичной скорости получим из формулы

, т.к. , то

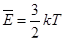
При одинаковых давлениях и температу­рах концентрация молекул всех газов одинакова. В частности, при нормальных условиях

Величину N_л называют числом Лошмидта, оно равно количеству молекул идеального газа, содержащихся в 1 м 3 газа при нор­мальных условиях.

6.Закрепление материала:

А) Вопросы для фронтального опроса:

1. Что такое макроскопические параметры? Какие величины относятся к их числу? Изменяется ли состояние системы при изменении одного такого параметра?

2. Какой газ называют идеальным? Что является моделью идеального газа?

3. При каких условиях газ по своим свойствам близок к идеальному? При каких условиях и почему газ не может считаться идеальным?

4. Что называют абсолютным нулем температуры? Каков физический смысл этого понятия с точки зрения молекулярно-кинетической теории?

5. Чему равно давление идеального га­за на стенки камеры при абсолют­ном нуле температуры?

6. Определите, чему равна температу­ра абсолютного нуля в градусах Цельсия. Возможно ли охладить те­ло до температуры абсолютного нуля?

7. Каково современное представление об энергии молекул при абсолютном нуле температуры?

8. Объясните принципы построения температурных шкал Цельсия и Кельвина. Сравните между собой эти шкалы и установите формулы, выражающие соотношение между значениями температуры, измерен­ной по шкалам Кельвина и Цельсия.

Б) Решение количественных задач:

Задача №1.

Найти концентрацию молекул кислорода, если его давление 0,2 МПа, а средняя квадратичная скорость молекул равна 700 м/с.

υ=700 м/с

Задача №2.

Задача №3.

Задача №4.

Сколько молекул содержится в 2 м 3 газа при давлении 150 кПа и температуре 27 ºС.(7,2·10 25 )

Задача №5.

На сколько процентов увеличивается средняя кинетическая энергия молекул газа при увеличении его температуры от 7 до 35 ºС? ( На 10%)

Задача №6.

Определить число n молекул, содержащихся в объеме V = 1 мм 3 воды и массу m₀ молекулы воды.

Число молекул n, содержащихся в теле некоторой массы m:

m₀ подсчитываем по формуле (3) ; .

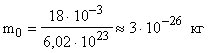
Задача №7.

Определить число молекул содержащихся в 10 г азота.

Задача №8.

Вычислить среднюю квадратичную скорость движения молекул водорода при 0 0 С.

Среднюю квадратичную скорость рассчитаем по формуле (17): .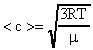

.

.

.

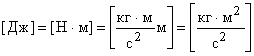
Задача №9.

Вычислить наиболее вероятную среднюю квадратичную и среднюю арифметическую скорости молекул азота при температуре 420 К.

При расчетах используем формулы (18), (17) и (19).

.

.

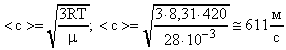
Задача №10.

Чему равна средняя квадратичная скорость движения молекул воздуха при температуре 27 0 С?

Среднюю квадратичную скорость молекул воздуха вычислим по формуле (17).

R = 8,31 .

.

Задача №11.

Вычислить среднюю энергию поступательного движения молекулы газа при 27 0 С.

Для расчета используем формулу (5).

.

.

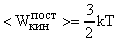
Задача №12.

Средняя квадратичная скорость молекул некоторого газа = 450 м/с. Давление газа р = 50 кПа. Найти плотность r газа при этих условиях.

Основное уравнение молекулярно-кинетической теории запишем в виде:

. Так как (масса газа); а (плотность газа), то или . Откуда .

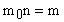
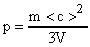
Расчет в Си: р = 5010 3 Па; = 450 м/с.

.

.

.

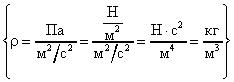
Задача №13.

Энергия поступательного движения молекул азота, находящегося в баллоне объемом V = 20л, 5 кДж, а средняя квадратичная скорость его молекул = 210 3 м/с. Найти массу m азота в баллоне и давление р под которым он находится.

Энергия поступательного движения молекул азота может быть выражена как , откуда . Известно, что (А). В формуле (А) заменим m. ; .

; .

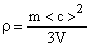
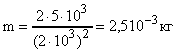
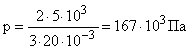
Задача №14.

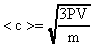
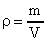
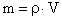
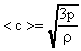
Для расчета используем формулу (16) (16). Так как и , то (после замены m) получаем ; .

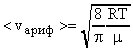
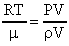
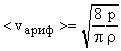
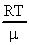
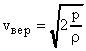
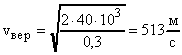
Формулу (19) можно преобразовать (19). Для этого заменим или, зная, что , получим ; . Окончательно имеем . Аналогично в формуле (18) заменим величину .

, .

; ; .

Задача №15. Средняя квадратичная скорость молекул некоторого газа при нормальных условиях = 461 м/с. Какое число молекул содержит единица массы этого газа?

. Так как , то . Найденное значение m₀ подставим в равенство (В). Окончательно получим:

.

.

Источник

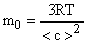
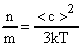
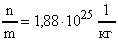
Назовите макроскопические параметры газа

Идеальный газ представляет собой простейшую модель газа, в которой пренебрегают энергией взаимодействия между отдельными частицами. Действительно, если газ достаточно разрежен, столкновения между его частицами происходят редко, в то время как скорости их велики, поэтому кинетическая энергия частиц значительно больше потенциальной энергии их взаимодействия.

Макроскопические параметры – величины, характеризующие состояние термодинамической системы без учета молекулярного строения тел

Давление в МКТ образуется из-за ударов молекул о стенки сосуда при тепловом движении.

Идеальный газ – модель газа, в которой молекулы считают материальными точками и не учитывают силы взаимодействия между ними.

Среднее значение квадрата скорости молекул

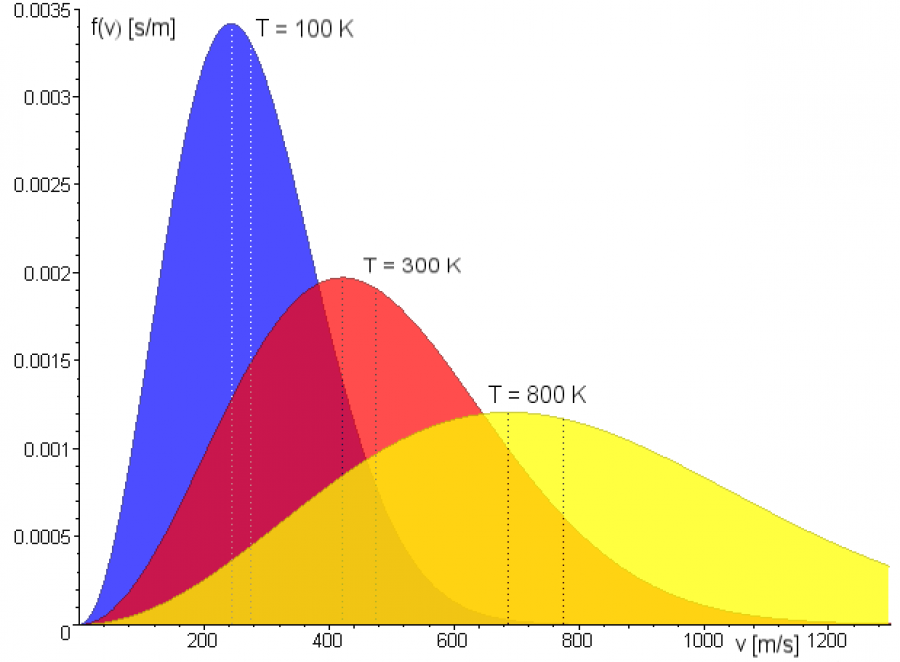
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Дж. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля.

С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υ_в и υ_кв увеличиваются.

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа.

Основное уравнение МКТ для идеального газа

Основное уравнение МКТ связывает макроскопические параметры состояния газа с характеристиками движения его молекул. Давление газа на стенки сосуда есть следствие столкновений молекул газа со стенками. Средняя сила, возникающая от совокупного действия всех молекул газа, определяет давление газа.

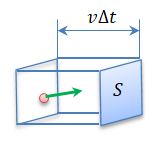
Представим себе сосуд в виде прямоугольного параллелепипеда, в котором содержится идеальный газ. Вычислим давление газа на одну из стенок сосуда площадью S.

N = 1/6 nV = 1/6 nSvΔt.

За время Δt полное изменение импульса составит Δp = Np₀ = 1/6 nSvΔt 2 m₀ v = 1/3 nSm₀ v 2

Сила, с которой молекулы воздействуют на стенку, F = Δp/ Δt

а давление, обусловленное этой силой, т.е. давление газа, равно p = F/S

Зависимость давления от концентрации и температуры

Средняя кинетическая энергия молекул

Концентрация

Закон Дальтона

В 1801 г. Джон Дальтон установил, что давление смеси нескольких газов равно сумме парциальных давлений всех газов, составляющих смесь. Этот закон получил название закона парциальных давлений газов. Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.

Воздух в комнате, где мы находимся, представляет собой смесь нескольких газов, в основном — азота (около 80%) и кислорода (около 20%). Парциальное давление каждого из этих газов — это давление, которое имел бы газ, если бы он один занимал весь объем. К примеру, если бы все газы, кроме азота, удалили из комнаты, то давление того, что осталось, и было бы парциальным давлением азота. Закон Дальтона утверждает, что общее давление всех газов вместе взятых равно сумме парциальных давлений каждого газа в отдельности.

Источник

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 15. Лекция 15. Идеальный газ

Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.

Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:

Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.

Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.

Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.

Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.

Модель идеального газа. Связь между давлением и средней кинетической энергией.

Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.

Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)

Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.

Свойства идеального газа:

Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.

Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.

До настоящего времени употребляются внесистемные единицы давления:

техническая атмосфера 1 ат = 9,81-104 Па;

физическая атмосфера 1 атм = 1,013-105 Па;

миллиметры ртутного столба 1 мм рт. ст.= 133 Па;

1 атм = = 760 мм рт. ст. = 1013 гПа.

Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени дей­ствует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.

Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.

Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.

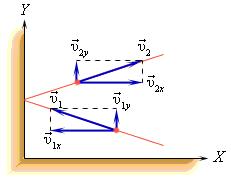
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ_y скорости, параллельная стенке, остается неизменной.

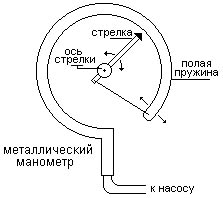
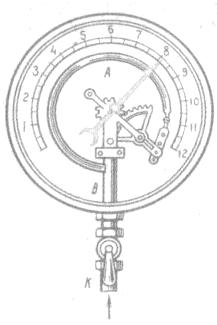
Приборы, измеряющие давление, называют манометрами. Манометры фиксиру­ют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.

Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул

n = N/V – число молекул в единице объема, или концентрация молекул;

Так как средняя кинетическая энергия поступательного движения молекул E = m₀*v 2 /2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m₀· v 2 )/2 = 2/3·E·n

Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.

Так как m₀·n = m₀·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v 2

Объединенный газовый закон.

Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.

Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.

Всякое изменение состояния газа называется термодинамическим процессом.

В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.

Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.

Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.

Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

где n – концентрация молекул, N – общее число молекул, V – объем газа

Тогда получим 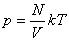или

Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит

При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.

Уравнение Клайперона можно записать в другой форме.

Здесь N – число молекул в сосуде, ν – количество вещества, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.

Ее численное значение в СИ R = 8,31 Дж/моль·К

называется уравнением состояния идеального газа.

В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`

Для одного моля любого газа это соотношение принимает вид: pV=RT

Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.

Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)

ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:

pS = F – сила давления.

Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.

Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.

Источник