Неравенства с параметрами и методы их решения

Урок «Неравенства с параметрами»

Краткое описание документа:

На этом уроке мы изучим алгоритм решения неравенств с параметрами и научимся применять его при решении такого типа заданий.

Определение первое.

Решить неравенство с параметром — значит для каждого значения параметра найти множество всех решений данного неравенства или доказать, что решений нет.

Рассмотрим линейные неравенства.

Определение второе.

Неравенства вида а икс плюс бэ больше нуля, больше либо равно нулю, меньше нуля, меньше либо равно нулю, где a и бэ — действительные числа, икс — переменная, называются неравенствами первой степени (линейными неравенствами).

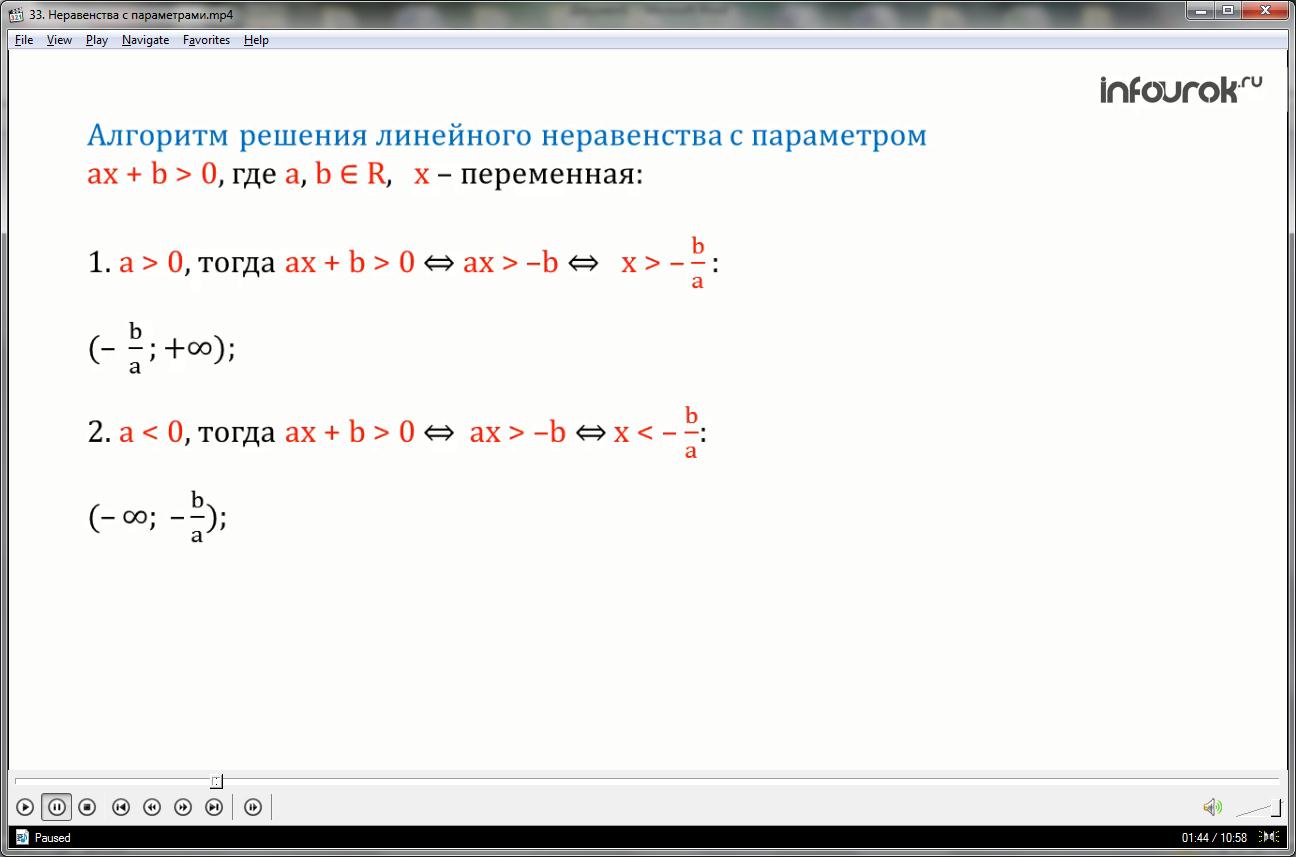
Алгоритм решения линейного неравенства с параметром, например, неравенстваа икс плюс бэ больше нуля, где a и бэ — действительные числа, икс — переменная. Рассмотрим следующие случаи:

Первый случай: a больше нуля, тогда икс больше минус бэ деленное на а.

Следовательно, множество решений неравенства есть открытый числовой луч от минус бэ деленное на а до плюс бесконечности.

Второй случай: a меньше нуля, тогда икс меньше минус бэ деленное на а

и, следовательно, множество решений неравенства есть открытый числовой луч от минус бесконечности до минус бэ деленное на а.

Третий случай: a равно нулю, тогда неравенство примет вид: ноль умноженное на икс плюс бэ больше нуля и для бэ большенуля любое действительное число есть решение неравенства, а при бэ меньшем либо равным нулю неравенство не имеет решений.

Остальные неравенства решаются аналогично.

Задание 1

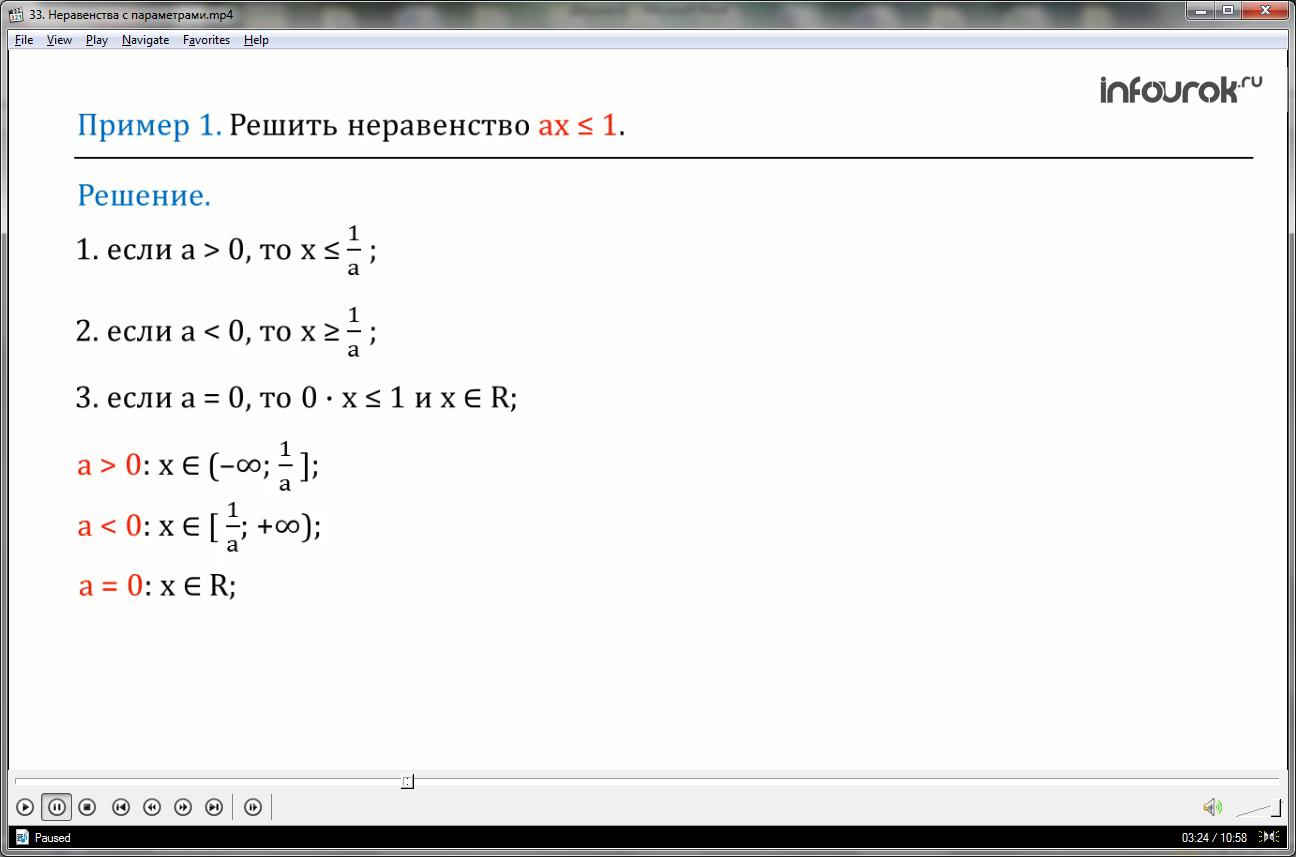
Решить неравенство а иксменьше либо равно единице.

Решение

В зависимости от знака a рассмотрим три случая.

Первый случай: если a больше нуля, то икс меньше либо равно один деленное на а;

Второй случай: если a меньше нуля, то икс больше либо равно один деленное на а;

Третий случай: если a равно нулю, то неравенство примет вид: ноль умноженное на икс меньше, либо равно единице и, следовательно, любое действительное число является решением исходного неравенства.

Таким образом, если а больше нуля, то икс принадлежит лучу от минус бесконечности до единицы, деленной на а.

Если a меньше нуля, то икс принадлежит лучу от единицы, деленной на а, до плюс бесконечности, и если a равно нулю,

то x принадлежит множеству действительных чисел.

Ответ: если а больше нуля, то икс принадлежит лучу от минус бесконечности до единицы, деленной на а;

если a меньше нуля, то икс принадлежит лучу от единицы, деленной на а, до плюс бесконечности, и если a равно нулю,

то x икс принадлежит множеству действительных чисел.

Задание 2

Решить неравенство модуль икс минус два больше минус квадрата разности а и единицы.

Решение

Заметим, что модуль икс минус два больше либо равно нулю для любого действительного икс и минус квадрат разности а и единицы меньше либо равно нулю для любого значения параметра a. Следовательно, если a равно единице, то любое икс — действительное число, отличное от двух, является решением неравенства, а если a не равно одному, то любое действительное число является решением неравенства.

Ответ: если a равно одному, то икс принадлежит объединению двух открытых числовых лучей от минус бесконечности до двух и от двух до плюс бесконечности,

а если a принадлежит объединению двух открытых числовых лучей от минус бесконечности до единицы и от одного до плюс бесконечности, то икс принадлежит множеству действительных чисел.

Задание 3

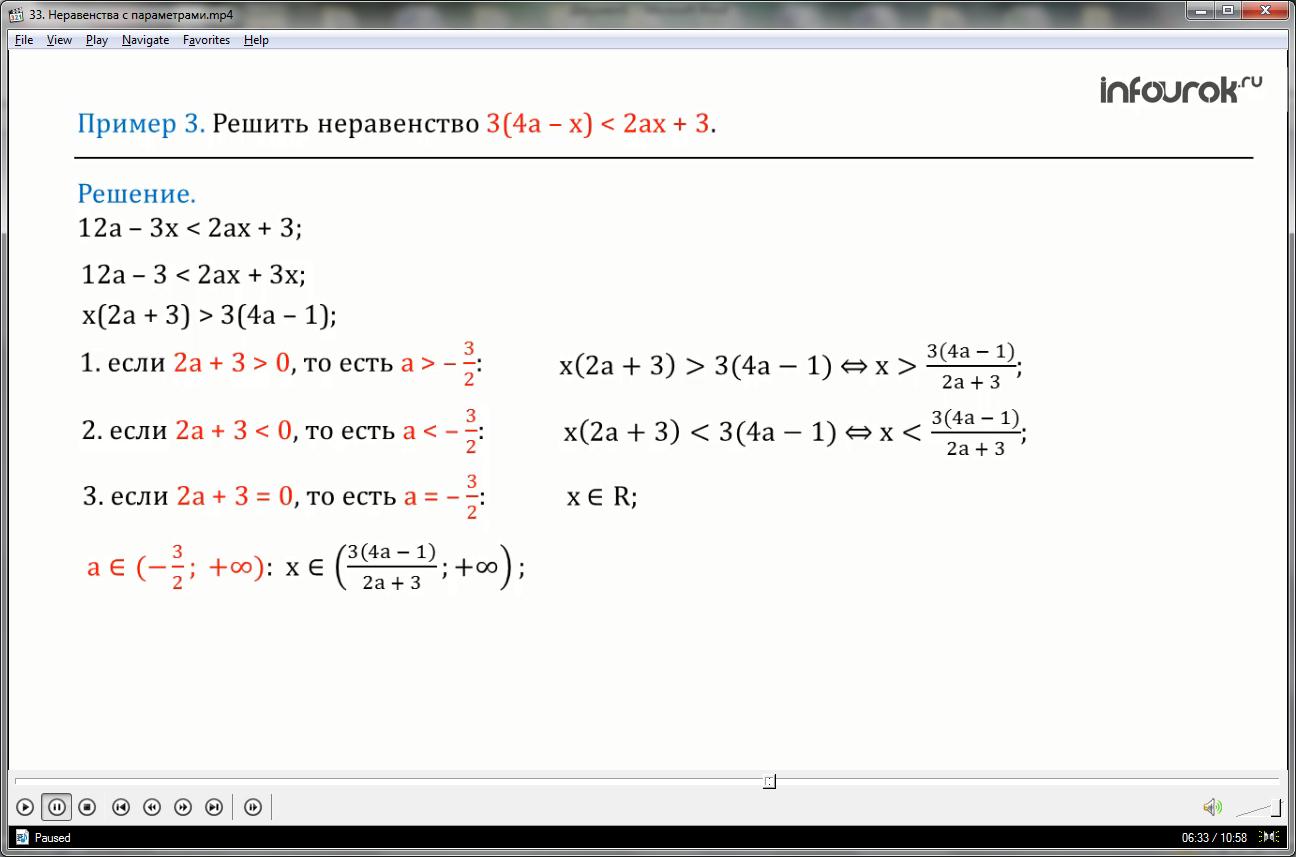
Решить неравенство три умноженное на разность четырех а и икса меньше двух а икс плюс три.

Решение

После элементарных преобразований данного неравенства, получим неравенство: икс умноженное на сумму двух а и трех больше три умноженное на разность четырех а и одного.

Далее рассмотрим три случая:

Первый случай: если два а плюс три больше нуля, то есть a больше минус трех вторых, то икс больше дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три.

Второй случай: если два а плюс три меньше нуля, то есть a меньше минус трех вторых, то икс меньше дроби, числитель которой — три умноженное на разность четырех а и одного, а знаменатель два а плюс три.

Третий случай: если два а плюс три равно нулю, то есть a равно минус три вторых,

любое действительное число является решением исходного неравенства.

Следовательно, если а принадлежит окрытому числовому лучу от минус трех вторых до плюс бесконечности, то икс

принадлежит открытому числовому лучу от дроби, числитель которой — три умноженное на разность четырех а и одного, а знаменатель — два а плюс три, до плюс бесконечности.

Если а принадлежит открытому числовому лучу от минус бесконечности до минус трех вторых, то икс принадлежит открытому числовому лучу от минус бесконечности до дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три;

если a равно минус трем вторых, то икс принадлежит множеству действительных чисел.

Ответ: если а принадлежит окрытому числовому лучу от минус трех вторых до плюс бесконечности, то икс

принадлежит открытому числовому лучу от дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три до плюс бесконечности;

если а принадлежит открытому числовому лучу от минус бесконечности до минус трех вторых, то икс принадлежит открытому числовому лучу от минус бесконечности до дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель два а плюс три;

если a равно минус трем вторых, то икс принадлежит множеству действительных чисел.

Задание 4

Для всех допустимых значений параметра а решить неравенство квадратный корень из икс минус а плюс квадратный корень из двух а минус икс плюс квадратный корень из а минус один плюс квадратный корень из трех минус а больше нуля.

Решение

Найдем область определения параметра а. Она определяется системой неравенств, решив которую находим, что а принадлежит отрезку от одного до трех.

Данное неравенство равносильно системе неравенств, решая которую находим, что икс принадлежит отрезку от а до двух а.

Если а принадлежит отрезку от единицы до трех, то решением исходного неравенства является отрезок от а до двух а.

Ответ: если а принадлежит отрезку от одного до трех, тоикс принадлежит отрезку от а до двух а.

Задание 5

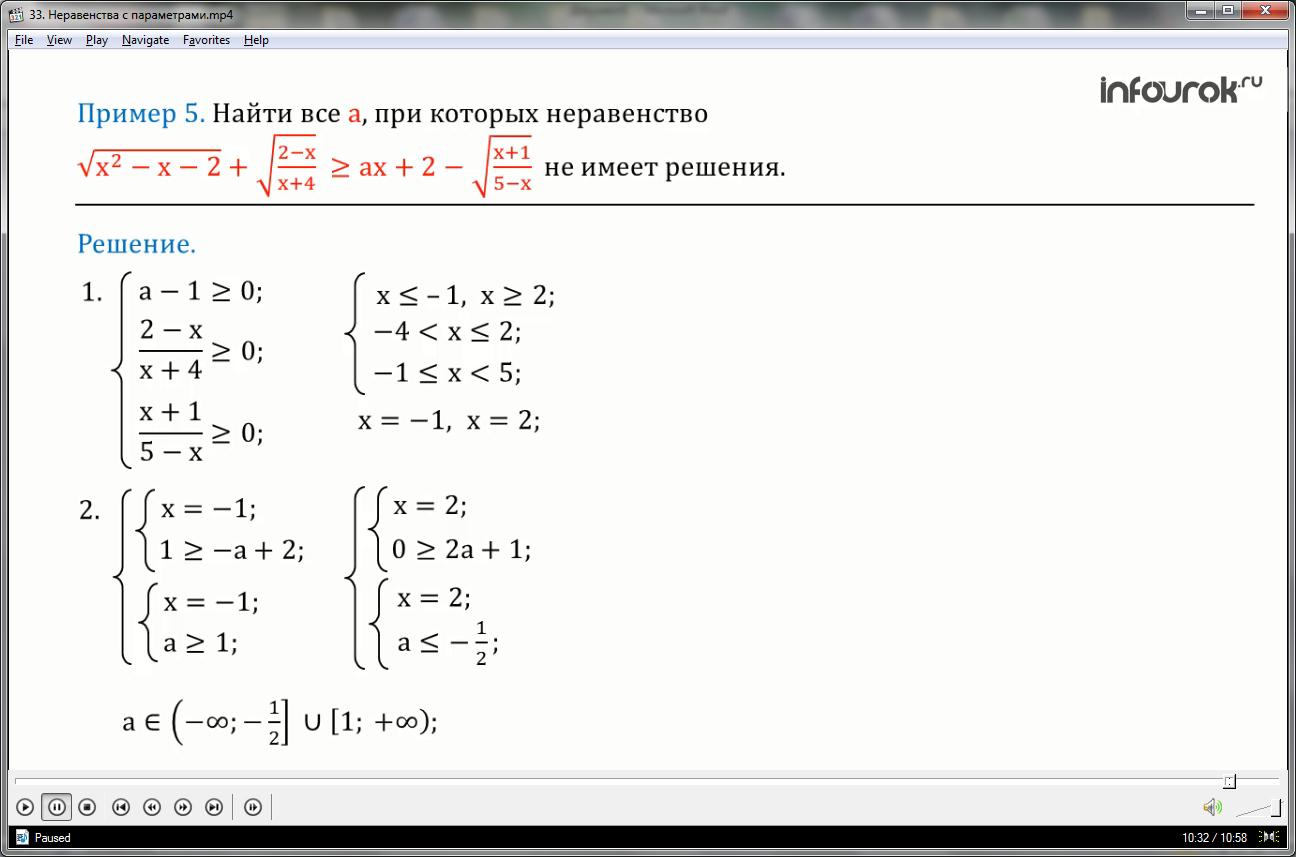
Найти все а, при которых неравенство

квадратный корень из икс в квадрате минус икс минус два плюс квадратный корень из дроби, числитель которой — два минус икс, а знаменатель — икс плюс четыре больше либо равно а икс плюс два минус квадратный корень из дроби, числитель которой — икс плюс один, а знаменатель — пять минус икс не имеет решения.

Решение

Первое. Вычислим область определения данного неравенства. Она определяется системой неравенств, решением которой являются два числа: икс равен минус единице и икс равен двум.

Второе. Найдем все значения а, при которых данное неравенство имеет решения. Для этого найдем все а, при которых икс равен минус единице и икс равен двум — это решение данного неравенства. Рассмотрим и решим совокупность двух систем. Решением является объединение двух числовых лучей от минус бесконечности до минус одной второй, и от единицы до плюс бесконечности.

Значит, данное неравенство имеет решение, если а принадлежит объединению двух числовых лучей от минус

бесконечности до минус одной второй, и от единицы до плюс бесконечности.

Третье. Следовательно, данное неравенство не имеет решения, если а принадлежит интервалу от минус одной второй до единицы.

Ответ: неравенство не имеет решения, если а принадлежит интервалу от минус одной второй до единицы.

Источник

Учебное пособие “Уравнения и неравенства с параметрами”

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В. Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

« Уравнения и неравенства с параметрами» для учащихся 10 –11 классов

данное пособие является приложением к программе элективного курса «Уравнения и неравенства с параметрами», которая прошла внешнюю экспертизу (научно-методическим экспертным советом министерства образования и науки Самарской области от 19 декабря 2008 года бала рекомендована к использованию в образовательных учреждениях Самарской области)

Авторы

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Ромаданова Ирина Владимировна

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Сербаева Ирина Алексеевна

Линейные уравнения и неравенства с параметрами……………..4-7

Квадратные уравнения и неравенства с параметрами……………7-9

Дробно- рациональные уравнения с параметрами……………..10-11

Иррациональные уравнения и неравенства с параметрами……11-13

Тригонометрические уравнения и неравенства с параметрами.14-15

Показательные уравнения и неравенства с параметрами………16-17

Логарифмические уравнения и неравенства с параметрами…. 16-18

Задания для самостоятельной работы…………………………. 21-28

Уравнения и неравенства с параметрами.

Если в уравнении или неравенстве некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Для того, чтобы решить уравнение или неравенство с параметрами необходимо:

Определить допустимые значения – это значения параметра, при которых уравнение или неравенство имеет смысл.

Решить уравнение или неравенство с параметрами означает:

1) определить, при каких значениях параметров существуют решения;

2) для каждой допустимой системы значений параметров найти соответствующее множество решений.

Решить уравнение с параметром можно следующими методами: аналитическим или графическим.

Аналитический метод предполагает задачу исследования уравнения рассмотрением нескольких случаев, ни один из которых нельзя упустить.

Решение уравнения и неравенства с параметрами каждого вида аналитическим методом предполагает подробный анализ ситуации и последовательное исследование, в ходе которого возникает необходимость «аккуратного обращения» с параметром.

Графический метод предполагает построение графика уравнения, по которому можно определить, как влияет соответственно, на решение уравнения изменение параметра. График подчас позволяет аналитически сформулировать необходимые и достаточные условия для решения поставленной задач. Графический метод решения особенно эффективен тогда, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра и обладает несомненным преимуществом увидеть это наглядно.

§ 1. Линейные уравнения и неравенства.

Линейное уравнение а x = b , записанное в общем виде, можно рассматривать как уравнение с параметрами, где x – неизвестное, a , b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра a является значение а = 0.

Если а ¹ 0, то при любой паре параметров а и b оно имеет единственное решение х=.

b = 0 является особым значением параметра b .

При b ¹ 0 уравнение решений не имеет.

При b = 0 уравнение примет вид: 0х = 0. Решением данного уравнения является любое действительное число.

Неравенства вида ах > b и ax b ( а ≠ 0) называются линейными неравенствами. Множество решений неравенства ах > b – промежуток

ах b множество решений – промежуток (-;), если a > 0, и (; +), если а

Пример 1. Решить уравнение ах = 5

Если а = 0, то уравнение 0 × х = 5 решения не имеет.

Ответ: при а ¹ 0, х=

при а = 0 решения нет.

Пример 2. Решить уравнение ах – 6 = 2а – 3х.

Решение: Это линейное уравнение, ах – 6 = 2а – 3х (1)

ах + 3х = 2а +6

Переписав уравнение в виде (а+3)х = 2(а+3), рассмотрим два случая:

Пример 3. При каких значениях параметра а среди корней уравнения

Решение: Решим уравнение 2ах – 4х – а 2 + 4а – 4 = 0 – линейное уравнение

При а = 2 решением уравнения 0х = 0 будет любое число, в том числе и большее 1.

При а ¹ 2 х =. По условию х > 1, то есть >1, а > 4.

Ответ: При а <2>U (4;∞).

Пример 4. Для каждого значения параметра а найти количество корней уравнения ах=8.

Решение. ах = 8 – линейное уравнение.

а =,

y = a – семейство горизонтальных прямых;

y = – графиком является гипербола. Построим графики этих функций.

Ответ: Если а =0, то уравнение решений не имеет. Если а ≠ 0, то уравнение имеет одно решение.

Пример 5. С помощью графиков выяснить, сколько корней имеет уравнение:

y = ах – 1 – графиком является прямая, проходящая через точку (0;-1).

Построим графики этих функций.

Ответ:При|а|>1– один корень

при | а|≤1 – уравнение корней не имеет.

Решение : ах + 4 > 2х + а 2 (а – 2) х > а 2 – 4. Рассмотрим три случая.

а > 2. (а – 2) х > ( а – 2)(а + 2) х > а + 2

а (а – 2) х > ( а – 2)(а + 2) х а + 2

Ответ. х > а + 2 при а > 2; х при а при а=2 решений нет.

§ 2. Квадратные уравнения и неравенства

Для решения квадратных уравнений с параметром можно использовать стандартные способы решения на применение следующих формул:

2) формул корней квадратного уравнения: х ₁ =, х ₂ =,

(х _{1,2 =} )

Квадратными называются неравенства вида

Множество решений неравенства (3) получается объединением множеств решений неравенства (1) и уравнения , a х 2 + b х + с=0. Аналогично находится множество решений неравенства (4).

Если квадратный трехчлен имеет корни (х _{1 2} ), то при а > 0 он положителен на множестве (-; х ₂ )( х _2; +) и отрицателен на интервале

(х ₁ ; х ₂ ). Если а ₁ ; х ₂ ) и отрицателен при всех х (-; х ₁ )( х _2; +).

Это квадратное уравнение

Решение: Особое значение а = 0.

При а = 0 получим линейное уравнение 2х – 4 = 0. Оно имеет единственный корень х = 2.

При а ≠ 0. Найдем дискриминант.

Пример 2. Найдите количество корней данного уравнения х²-2х-8-а=0 в зависимости от значений параметра а.

Решение. Перепишем данное уравнение в виде х²-2х-8=а

y = х²-2х-8– графиком является парабола;

y =а– семейство горизонтальных прямых.

Построим графики функций.

Решение. Квадратный трехчлен положителен при всех значениях х, если

§ 3. Дробно- рациональные уравнения с параметром,

сводящиеся к линейным

Процесс решения дробных уравнений выполняется по обычной схеме: дробное заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решается целое уравнение, исключая посторонние корни, то есть числа, которые обращают знаменатель в нуль.

В случае уравнений с параметром эта задача более сложная. Здесь, чтобы «исключить» посторонние корни, требуется найти значение параметра, обращающее общий знаменатель в нуль, то есть решить соответствующие уравнения относительно параметра.

Пример 1. Решить уравнение = 0

Это дробно- рациональное уравнение

Пример 2 . Решить уравнение– = (1)

Это дробно- рациональное уравнение

При переходе от уравнения (1) к уравнению (2) расширилась область определения уравнения (1), что могло привести к появлению посторонних корней. Поэтому, необходима проверка.

П р о в е р к а. Исключим из найденных значений х такие, при которых

х ₁+1=0, х ₁+2=0, х₂+1=0, х₂+2=0.

Если х₂+1=0, то есть (а – 3) + 1= 0, то а = 2. Таким образом, при а = 2 х₂ – посторонний корень уравнения (1).

Если х₂+2=0, то есть (а – 3) + 2 = 0, то а=1. Таким образом, при а = 1,

Можно записать ответ.

§4. Иррациональные уравнения и неравенства

Уравнения и неравенства, в которых переменная содержится под знаком корня, называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение, учитывая при этом изменения значений параметра.

Уравнение вида = g ( x ) равносильно системе

Неравенство f ( x ) ≥ 0 следует из уравнения f ( x ) = g 2 ( x ).

При решении иррациональных неравенств будем использовать следующие равносильные преобразования:

≤ g(x) ≥g(x)

Пример 1. Решите уравнение = х + 1 (3)

Это иррациональное уравнение

Решение: По определению арифметического корня уравнение (3) равносильно системе .

При а = 2 первое уравнение системы имеет вид 0 х = 5, то есть не имеет решений.

откуда а ≤ или а > 2.

Ответ: При а≤, а > 2 х= , при уравнение решений не имеет.

Пример 2. Решить уравнение = а (приложение 4)

Решение. y =

y = а – семейство горизонтальных прямых.

Построим графики функций.

Решение. О.Д.З. х ≤ 2. Если а+1 ≤0, то неравенство выполняется при всех допустимых значениях х. Если же а+1>0, то

(а+1)

откуда х (2- 2

§ 5. Тригонометрические уравнения и неравенства.

Приведем формулы решений простейших тригонометрических уравнений:

Sinx = a x= (-1) n arcsin a+πn, n Z, ≤1, (1)

tg x = a x= arctg a + πn, n Z, aR

ctg x = a x = arcctg a + πn, n Z, aR

Для каждого стандартного неравенства укажем множество решений:

1. sin x > a arcsin a + 2 πn Z,

при a xR ; при a ≥ 1, решений нет.

при а≤-1, решений нет; при а >1, xR

3. cos x > a – arccos a + 2 πn x arccos a + 2 πn , n Z ,

5. tg x > a, arctg a + πnZ

Пример1. Найти а, при которых данное уравнение имеет решение:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Решение. Запишем уравнение в виде

Ответ. а -2; 0 4; 6

Пример 2. При каких b найдется а такое, что неравенство + b > 0 выполняется при всех х ≠ πn , n Z .

Решение. Положим а = 0. Неравенство выполняется при b >0. Покажем теперь, что ни одно b ≤0 не удовлетворяет условиям задачи. Действительно, достаточно положить х = π /2, если а π /2 при а ≥0.

§ 6. Показательные уравнения и неравенства

1. Уравнение h ( x ) f ( x ) = h ( x ) g ( x ) при h ( x ) > 0 равносильно совокупности двух систем и

2. В частном случае ( h ( x )= a ) уравнение а f ( x ) = а g ( x ) при а > 0, равносильно совокупности двух систем

и

3. Уравнение а f ( x ) = b , где а > 0, a ≠1, b >0, равносильно уравнению

Решение простейших показательных неравенств основано на свойстве степени. Неравенство вида f ( a x ) > 0 при помощи замены переменной t = a x сводится к решению системы неравенств а затем к решению соответствующих простейших показательных неравенств.

Пример 1 . При каких а уравнение 8 х = имеет только положительные корни?

Решение. По свойству показательной функции с основанием, большим единицы, имеем х>0 8 х >1 >1 >0, откуда a (1,5;4).

Ответ. a (1,5;4).

Решение. Рассмотрим три случая:

§ 7. Логарифмические уравнения и неравенства

Приведем некоторые эквивалентности, используемые при решении логарифмических уравнений и неравенств.

В частности, если а >0, а ≠1, то

log _a g (x)= log _a h(x)

2. Уравнение log _a g (x)=b g (x)= a b ( а >0, a ≠ 1, g(x) >0).

3. Неравенство log _{f ( x )} g ( x ) ≤ log _{f ( x )} h ( x ) равносильно совокупности двух систем: и

Если а, b – числа, а >0, а ≠1, то

log _a f (x) ≤ b

log _a f (x) > b

_{Пример 1. Решите уравнение}

Пример 2. Найдите наибольшее значение а, при котором уравнение

2 log – + a = 0 имеет решения.

При а = квадратное уравнение имеет корень t = >0.

Ответ. а =

Решение. Решим систему неравенств

Корни квадратных трехчленов х _1,2 = 1 ± и х _3,4 = 1 ±.

Критические значения параметра : а = 1 и а = 9.

Пусть Х₁ и Х₂ – множества решений первого и второго неравенств, тогда

Х ₁ Х ₂ = Х – решение исходного неравенства.

Рассмотрим три случая:

3. a ≥ 9 Х – решений нет.

Высокий уровень С1, С2

Пример 1. Найдите все значения р, при которых уравнение

р ∙ ctg 2 x + 2 sinx + p = 3 имеет хотя бы один корень.

Решение. Преобразуем уравнение

При t , E ( f ) = ,

При t , E ( f ) = , то есть при t , E ( f ) = .

Чтобы уравнение 3 t 2 – 2 t 3 = p ( следовательно, и данное) имело хотя бы один корень необходимо и достаточно p E ( f ), то есть p .

Ответ. .

При каких значениях параметра а уравнение log (4 x 2 – 4 a + a 2 +7) = 2 имеет ровно один корень?

Решение. Преобразуем уравнение в равносильное данному:

Отметим, что если некоторое число х является корнем полученного уравнения, то число – х также является корнем этого уравнения. По условию это не выполнимо, поэтому единственным корнем является число 0.

1) a ₁ = 1. Тогда уравнение имеет вид: log (4 x 2 +4) =2. Решаем его

2) a ₂ = 3. Уравнение имеет вид: log (4 x 2 +4) =2 х = 0 – единственный корень.

Высокий уровень С4, С5

Пример 3. Найдите все значения р, при которых уравнение

Пример 4. Найдите все положительные значения параметра а, при которых число 1 принадлежит области определения функции

Если значения х = 1 принадлежит области определения, то должно выполняться неравенство а– а ≥ 0, а≥ а (1)

Таким образом, необходимо найти все а > 0, удовлетворяющие неравенству (1).

1) а = 1 удовлетворяет неравенству (1).

2) При а > 1 неравенство (1) равносильно неравенству 2 + 5а ≥ а 2 +6,

Источник