Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных
Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений 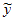
Эконометрика : учеб. / под ред. И.И. Елисеевой. – М. : Проспект, 2009. – С. 82–89.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М. : Проспект, 2008. – С. 93–112.
Магнус, Ян Р. Эконометрика: начальный курс: Учебник для студ-ов вузов, обуч. по экон. спец. / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий; Акад. народ. хоз-ва при Правительстве Рос. Федерации. – М. : Дело, 2000. – С. 130–135.
ответ тест i-exam
Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками



+: автокоррелированными и/или гетероскедастичными
-гомоскедастичными и некоррелированными
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
+: линейной
-надежности среднеквадратической ошибки
-ненадежности среднеквадратической ошибки
+: ненадежности оценки
детерминации для модели в исходных показателях равен … Варианты ответов
+: 0,64
При методе наименьших квадратов параметры уравнения парной линейной регрессии 

равенства нулю суммы квадратов
+ минимизации суммы квадратов
125 Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 


+ положительной
126 Исходная регрессионная модель имеет вид 

предпосылки МНК нарушены; традиционного
предпосылки МНК не нарушены; обобщенного
предпосылки МНК не нарушены; традиционного
+ предпосылки МНК нарушены; обобщенного
Если известно уравнение множественной регрессии 
+766,67
Тема208: Обобщенный метод наименьших квадратов (ОМНК)
Пустьy– издержки производства, 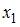
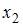
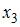
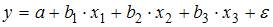
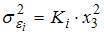
После применения обобщенного метода наименьших квадратов новая модель приняла вид 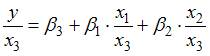
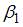





Тема219: Временные ряды данных: характеристики и общие понятия
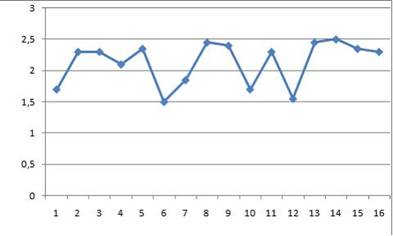
Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Варианты ответов

Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции 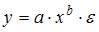
Варианты ответов





Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для стационарных временных рядов y1, у2, … yt, …, yn (t = 1, …, n) автокорреляция зависит только от величины …
Варианты ответов





1)Тема: Предпосылки МНК, методы их проверки
Предпосылками метода наименьших квадратов (МНК) являются следующие …(не менее 2 вариантов ответа)
Варианты ответов
+ 1 отсутствие автокорреляции в остатках
2 присутствие в эконометрической модели более чем двух факторов
3 функциональная связь между зависимой и независимой переменными
+ 4 гомоскедастичность остатков
2)Тема: Оценка параметров линейных уравнений регрессии
Метод наименьших квадратов применим к уравнениям регрессии, …(не менее 2 вариантов ответа)
Варианты ответов
1 которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду
+2 которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду
3 нелинейного вида
+4 которые отражают линейную зависимость между двумя экономическими показателями
3) Тема: Обобщенный метод наименьших квадратов (ОМНК)
Обобщенный метод наименьших квадратов подразумевает … (не менее 2 вариантов ответа)
Варианты ответов
1 переход от множественной регрессии к парной
+2 преобразование переменных
+3 введение в выражение для дисперсии остатков коэффициента пропорциональности
4 двухэтапное применение метода наименьших квадратов
2) Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Несмещенность оценки характеризуется …(не менее 2 вариантов ответа)
Варианты ответов
1 зависимостью от объема выборки значения математического ожидания остатков
+2 равенством нулю математического ожидания остатков
3 максимальной дисперсией остатков
+ 4 отсутствием накопления остатков при большом числе выборочных оцениваний
111.Тема: Структура временного ряда
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
между трендовой, сезонной и случайной компонентами
+первого, второго, третьего и последующих порядков
факторов, формирующих уровень ряда между несколькими временными рядами
118.Тема: Обобщенный метод наименьших квадратов (ОМНК)
При оценке параметров регрессионной модели с гетероскедастичными остатками при помощи обобщенного метода наименьших квадратов (ОМНК) выдвигается предположение, что дисперсия остатков …
+пропорциональна некоторой величине
СОДЕРЖАНИЕ
Схема метода
где последние два члена оцениваются как скаляры, в результате чего
Следовательно, минимум целевой функции можно вычислить, получив явную формулу:
Характеристики
Взвешенный метод наименьших квадратов
Возможные обобщенные методы наименьших квадратов
В общем, этот оценщик имеет свойства, отличные от GLS. Для больших выборок (т. Е. Асимптотически) все свойства (при соответствующих условиях) являются общими по отношению к GLS, но для конечных выборок свойства оценок FGLS неизвестны: они сильно различаются для каждой конкретной модели и, как правило, их точные распределения не может быть получен аналитически. Для конечных выборок FGLS может быть даже менее эффективным, чем OLS в некоторых случаях. Таким образом, хотя GLS можно сделать осуществимым, не всегда разумно применять этот метод, когда образец небольшой. Метод, который иногда используется для повышения точности оценок в конечных выборках, заключается в повторении, то есть взятии остатков из FGLS для обновления оценки ковариации ошибок, а затем обновлении оценки FGLS, итеративно применяя ту же идею до тех пор, пока оценки не изменятся меньше, чем некоторые толерантность. Но этот метод не обязательно значительно повышает эффективность оценщика, если исходная выборка была небольшой. Разумным вариантом, когда выборки не слишком большие, является применение МНК, но отказ от классической оценки дисперсии.
Важно отметить, что возведенные в квадрат остатки нельзя использовать в предыдущем выражении; нам нужен оценщик дисперсии ошибок. Для этого мы можем использовать параметрическую модель гетероскедастичности или непараметрическую оценку. Как только этот шаг будет выполнен, мы можем продолжить:
Оценка с помощью с помощью взвешенных наименьших квадратов β F грамм L S 1 <\ displaystyle \ beta _ 
Процедуру можно повторять. Первая итерация дается формулой
Эту оценку можно повторить до сходимости. Ω ^ <\ displaystyle <\ widehat <\ Omega>>>
В условиях регулярности любая оценка FGLS (или оценка любой из ее итераций, если мы повторяем конечное число раз) асимптотически распределена как
Обобщенный метод наименьших квадратов (ОМНК)
Если при использовании классического метода наименьших квадратов обнаруживается наличие гетероскедастичности и автокорреляции ошибок, т.е. нарушаются предпосылки МНК 2 и 3, то рекомендуется использовать обобщенный метод наименьших квадратов (ОМНК).
При моделировании реальных экономических процессов довольно часто возникают такие ситуации, в которых условия классической линейной модели регрессии оказываются нарушенными, в частности, что случайные возмущения (ошибки) модели имеют постоянную дисперсию и не коррелированны между собой. Так, например, при использовании зависимости расходов на потребление от уровня доходов семьи можно ожидать, что в более обеспеченных семьях вариация расходов выше, чем в малообеспеченных, т.е. дисперсии возмущения не одинаковы. При рассмотрении временных рядов сталкиваются с ситуацией, когда наблюдаемые в данный момент значения зависимой переменной коррелируют с их значениями в предыдущие моменты времени, т.е. наблюдается корреляция между возмущениями в разные моменты времени.
Сравнивая обобщенную модель с классической, можно отметить, что главное их отличие заключается в том, что в обобщенной модели ковариации и дисперсии объясняющих переменных х могут быть произвольными.
Сущность ОМНК заключается в том, что он применяется к преобразованным данным и позволяет получить оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. То есть как и ранее предполагается, что среднее значение возмущений (ошибок) равно нулю, а вот дисперсия их не остается неизменной для разных значений факторов, а пропорциональна величине Кр
где S^ — дисперсия ошибок при конкретном /-м значении фактора;
S 2 — постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
Kt — коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обуславливает непропорциональность остатков.
Так, для уравнения вида 
где остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастич- ными остатками, поделив все переменные, зафиксированные в ходе
/-го наблюдения на 
Исходные данные для полученного уравнения будут иметь вид
Оценка параметров нового уравнения с преобразованными переменными проводится с помощью МНК, для которого необходимо минимизировать сумму квадратов отклонений:
Соответственно получим следующую систему нормальных уравнений:
Аналогичный подход возможен не только для уравнений парной регрессии, но и для множественной, например, вида
для которой дисперсия ошибок оказалась пропорциональна Kh таким образом, при
Однако при применении ОМНК в таком виде могут возникнуть определенные трудности, так как в практике эконометрического моделирования крайне редко бывает так, чтобы была известна постоянная дисперсия ошибки S 2 и соответственно коэффициент пропорциональности Ki для исходных данных (у,*,-), по которому можно было бы произвести их дисконтирование с целью корректировки гетероскедастичности. Использование тестов на гетероскедастичность (например, рассмотренный выше тест Голдфелда — Квандта) позволяет обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности. В такой ситуации для продвижения к цели, очевидно, необходимы некоторые дополнительные предположения относительно характера гетероскедастичности.
На практике при построении эконометрических моделей возможно применение методов смягчения проблемы гетероскедастичности. Одним из таких методов является метод взвешенных наименьших квадратов (ВНК). В соответствии с ним возможны два вида преобразования модели с целью устранения проблемы гетероскеда- стичности:
Таким образом, применяя обычный МНК, неизвестные параметры регрессионной модели находятся путем минимизации остаточной суммы квадратов 

Для случая применения ВНК, когда для каждого наблюдения известны значения дисперсии фактической ошибки S 2 e., можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. Рассмотрим применение данного случая для ВНК на примере парной регрессии
Разделим обе части уравнения регрессии на известное
Положив 
Таким образом, ВНК включает следующие этапы:
б) по МНК для преобразованных значений 
уравнение регрессии без свободного члена с гарантированными качествами оценок.
Например, может оказаться целесообразным предположить, что дисперсии S?. пропорциональны значениям (рис. 5.6а) или значениям х 2 (рис. 5.66).
Рис. 5.6. Пропорциональность дисперсий фактических ошибок со значением факторного признака
Дисперсия 
Тогда уравнение преобразуется делением его левой и правой части на 
где
Дисперсия 

В этом случае, если зависимость 
Для применения описанных выше преобразований весьма значимы знания об «истинных» значениях дисперсий отклонений, либо предположения, какими эти дисперсии могут быть. Во многих случаях дисперсии отклонений зависят не от включенных в уравнение регрессии объясняющих переменных, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. В этом случае они должны быть включены в модель. В ряде случаев для устранения гетероскедастичности необходимо изменить спецификацию модели (например, линейную на лог-линейную, мультипликативную на аддитивную и т.п.).
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности является достаточно трудоемкой проблемой, и для ее решения разработано несколько методов (тестов). В случае установления наличия гетероскедастичности ее корректировка также является достаточно серьезной проблемой. Одним из возможных решений является метод взвешенных наименьших квадратов (при этом необходимы определенная информация либо обоснованные предположения о величинах дисперсий отклонений).
На практике имеет смысл применить несколько методов определения гетероскедастичности и способов ее корректировки.