шарик подвешен на невесомой нерастяжимой нити длиной 2 м какую минимальную скорость следует сообщить
Задача 1: минимальная скорость, необходимая для полного оборота шара
Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?
Эта задача была размещена посетителями в разделе Решаем вместе 25 мая 2007 года.
Воспользуемся законом сохранения механической энергии при переходе шарика из нижнего положения в верхнее:
| mvo 2 | = mg • 2l + | mv 2 | (1), |
| 2 | 2 |
где l — длина подвеса или нерастяжимой нити.
В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса:
Поскольку шарик достиг верхней точки (T = 0, условие задачи), то
| mv 2 | = mg |
| l |
отсюда
Сделаем подстановку (2) в (1), получим
| mvo 2 | = 2mgl + | mgl |
| 2 | 2 |
vo 2 = g4l + gl = 5gl.
Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Примечание: если шар подвешен на жестком стержне, то в верхней точке скорость v может обратиться в нуль, тогда из (1)
| mvo 2 | = mg•2l, отсюда |
| 2 |
Произведя вычисления, получим: vo = 2×√(10×0,5) = 4,47 (м/с).
Шарик подвешен на невесомой нерастяжимой нити длиной 2 м. Какую минимальную скорость следует сообщить шарику, чтобы он описал окружность в вертикальной плоскости? Сопротивлением воздуха пренебречь.
Ответ:
Объяснение:
Электрическое и магнитное поля вибратора. Неквазистационарный характер колебаний в открытом вибраторе приводит к тому, что создаваемые отдельными его участками поля на некотором расстоянии от вибратора уже не компенсируют друг друга, как это имеет место для «закрытого» колебательного контура с сосредоточенными параметрами, где колебания квазистационарны, электрическое поле целиком сосредоточено внутри конденсатора, а магнитное — внутри катушки. Из-за такого пространственного разделения электрического и магнитного полей они непосредственно не связаны друг с другом: их взаимное превращение обусловлено только током — переносом заряда по контуру.
У открытого вибратора, где электрическое и магнитное поля перекрываются в пространстве, происходит их взаимное влияние: изменяющееся магнитное поле порождает вихревое электрическое поле, а изменяющееся электрическое поле порождает магнитное поле. В результате оказывается возможным существование таких «самоподдерживающихся» и распространяющихся в свободном пространстве полей на большом расстоянии от вибратора. Это и есть излучаемые вибратором электромагнитные волны.
Опыты Герца. Вибратор, с помощью которого Г. Герцем в 1888 г. впервые были экспериментально получены электромагнитные волны, представлял собой прямолинейный проводник с небольшим воздушным промежутком посредине (рис. 178а). Благодаря такому промежутку можно было сообщить двум половинам вибратора значительные заряды. Когда разность потенциалов достигала определенного предельного значения, в воздушном зазоре возникал пробой (проскакивала искра) и электрические заряды через ионизированный воздух могли перетекать с одной половины вибратора на другую. Б открытом контуре возникали электромагнитные колебания. Чтобы быстропеременные токи существовали только в вибраторе и не замыкались через источник питания, между вибратором и источником включались дроссели (см. рис. 178а).
Шарик подвешен на невесомой нерастяжимой нити длиной 2 м какую минимальную скорость следует сообщить
невесомая нерастяжимая нить
Два груза, массы которых равны m1 = 0,9 кг и m2 = 0,20 кг, связаны невесомой и нерастяжимой нитью и лежат на гладкой доске. К левому грузу приложена сила F1 = 5,3 Н, к правому в противоположном направлении, — F2 = 2,9 Н. Найти силу натяжения нити Т при движении грузов.
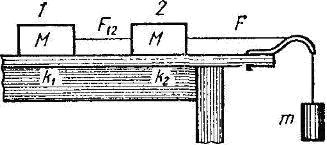
На горизонтальном столе лежат два тела массы М = 1,000 кг каждое. Тела связаны невесомой нерастяжимой нитью. Такая же нить связывает тело 2 с грузом массы m = 0,500 кг. Нить может скользить без трения по изогнутому желобу, укрепленному на краю стола. Коэффициент трения первого тела со столом k1 = 0,100, второго тела k2 = 0,150. Найти: а) ускорение w, с которым движутся тела, б) натяжение F12 нити, связывающей тела 1 и 2, в) натяжение F нити, на которой висит груз.
На блок (однородный диск) массой m0 и радиусом R намотана невесомая нерастяжимая нить, к концу которой привязан груз массой m. В оси блока имеется трение. Найти момент силы трения, если за время t после начала движения груз опустился на расстояние h.
На конце невесомой нерастяжимой нити длиной 1,5 м подвешен шар массой 1,3 кг. В шар попадает и застревает в нем летящая горизонтально со скоростью 47 м/с пластиковая пуля массой 13 г. На какую высоту поднимется шар?
Шарик подвешен на невесомой нерастяжимой нити длиной 2 м. Какую минимальную скорость следует сообщить шарику, чтобы он описал окружность в вертикальной плоскости? Сопротивлением воздуха пренебречь?
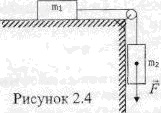
Вычислите ускорения тел и силу натяжения нити (рисунок 2.4). Нить невесомая, нерастяжимая, блок невесомый, m1 = 1 кг, m2 = 2 кг, коэффициент трения первого тела о поверхность μ = 0,1, внешняя сила F = 10 Н.
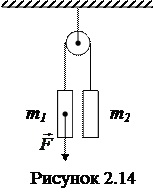
Вычислите ускорение тел и силу натяжения нити (рисунок 2.14). Нити невесомые, нерастяжимые, блок невесомый, массы тел m1 = 1 кг, m2 = 2 кг, внешняя сила F = 6 Н.
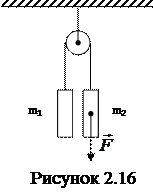
Вычислите ускорение тел и силу натяжения нити (рисунок 2.16). Нити невесомые, нерастяжимые, блок невесомый, массы тел m1 = 1 кг, m2 = 2 кг, внешняя сила F = 6 Н.
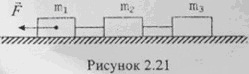
Вычислите ускорения тел и силы натяжения нитей (рисунок 2.21). Нити невесомые и нерастяжимые, m1 = 1 кг, m2 = 2 кг, m3 = 3 кг, внешняя сила F = 15 Н, коэффициенты трения тел о поверхность μ1 = 0,3, μ2 = 0,2, μ3 = 0,3.
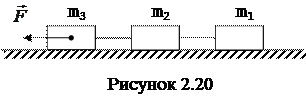
Вычислите ускорения тел и силы натяжения нитей (рисунок 2.20). Нити невесомые и нерастяжимые, m1 = 1 кг, m2 = 2 кг, m3 = 3 кг, внешняя сила F = 15 Н, коэффициенты трения тел о поверхность μ1 = μ2 = μ3 = 0,1.
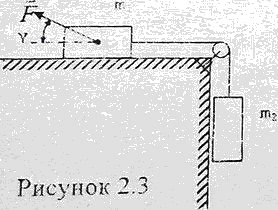
Вычислите ускорения грузов и силу натяжения нити (рисунок 2.3). Нить нерастяжимая, невесомая, блок невесомый, m1 = 1 кг, m2 = 2 кг, коэффициент трения первого тела о поверхность μ = 0,1, внешняя сила F = 10 Н, угол γ = 60°.
Какую минимальную горизонтальную скорость надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости? Шар подвешен на нерастяжимой и невесомой нити длиной l = 0,4 м.
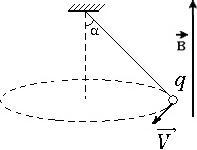
Шарик массой m = 10 г и зарядом q = 5·10 –2 Кл, подвешенный на невесомой нерастяжимой нити, равномерно вращается по окружности в горизонтальной плоскости (см. рисунок). Найти радиус окружности, если скорость шарика v = 1 м/с. Учесть, что имеется однородное магнитное поле с индукцией В = 1 Тл, линии которого направлены вертикально вверх. Угол α = 45°.
Три одинаковых кубика, связанные невесомыми и нерастяжимыми нитями, движутся по гладкому горизонтальному столу под действием горизонтальной силы F, приложенной к первому кубику. Чему равны силы натяжения нитей, связывающей первый и второй, второй и третий кубики?
Шарик подвешен на невесомой нерастяжимой нити длиной 2 м какую минимальную скорость следует сообщить
Шарик массой m = 400 г, подвешенный на невесомой нерастяжимой нити длиной l = 80 см, отвели в сторону от положения равновесия и отпустили. Нить обрывается при силе натяжения T0 = 12 Н. При прохождении положения равновесия нить оборвалась, и шарик абсолютно неупруго столкнулся с покоившимся на гладкой поверхности стола бруском. После удара брусок приобрел скорость u = 0,8 м/с. Найдите массу бруска M.
1. Непосредственно перед обрывом нити в момент прохождения положения равновесия шарик движется по окружности радиусом l со скоростью В этот момент действующие на шарик сила тяжести
и сила натяжения нити
направлены по вертикали и вызывают центростремительное ускорение шарика (см. рисунок). Запишем второй закон Ньютона в проекциях на ось Oy инерциальной системы отсчёта Oxy, связанной с Землёй:
откуда
2. При прохождении положения равновесия нить обрывается, и шарик, движущийся горизонтально со скоростью абсолютно неупруго сталкивается с покоящимся бруском. При столкновении сохраняется импульс системы шарик — брусок. В проекциях на ось Ox получаем:
где u — проекция скорости бруска с шариком после удара на эту ось. Отсюда:
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона, формула центростремительного ускорения, закон сохранения импульса системы); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины | 3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.). В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. Отсутствует пункт IV, или в нём допущена ошибка | 2 |
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. Шарик подвешен на невесомой нерастяжимой нити длиной 2 м какую минимальную скорость следует сообщитьПри ударе пули о шар действует закон сохранения импульса, который выглядит следующим образом: где Далее система начинает двигаться по окружности радиусом l. В нижней точке траектории она обладает только кинетической энергией, а в верхней — и кинетической и потенциальной. По закону сохранения энергии: Рассмотрим силы, которые действуют на систему в верхней точке. Шар с пулей вращается за счет центростремительного ускорения, направленного к центру окружности. Оно в свою очередь порождается действующими на тело силой тяжести и силой натяжения нити направленными вертикально вниз. Граничное условие, при котором тело не падает, а продолжает вращаться — это нулевое натяжение нити. Тогда: Подставляя это выражение в предыдущее уравнение получаем: И из закона сохранения импульса находим начальную скорость пули:
|