Как решить уравнение с параметром 7 класс

Линейные уравнения с параметрами в 7-м классе (методические рекомендации)

Разделы: Математика

а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.

а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.

Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.

Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если а=10; а=-2; а=0.

Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра а

Как было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
Решение.1) (а2-1)=0, а=±1.
При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.

Задачи для самостоятельного решения.

Для всех значений параметров а и в решите уравнения:

Используемая литература.

Источник

Решение уравнений с параметрами 7 класс

в данной публикации содержатся примеры решения линейных уравнений с параметрами для учащихся 7 класса.

Просмотр содержимого документа
«Решение уравнений с параметрами 7 класс»

Примеры решения линейных уравнений, содержащие параметры.

Линейные уравнения с одним неизвестным могут содержать и другие буквы. Такие уравнения называют уравнениями с параметрами. Уравнения, содержащие параметры, решаются также, как и обычные линейные уравнения, но корни уравнения зависят от значений параметров и выражаются через них.

Пример 1. Решим уравнение относительно переменной x:

Перенесем члены уравнения, содержащие x, в левую часть, а все остальные – в правую часть уравнения:

Вынесем x в левой части за скобки:

При p = 5 получаем 0  x = 22, т.е. уравнение корней не имеет.

Если же p ≠ 5, то разделим обе части уравнения на 5 – p.

x = 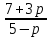– уравнение имеет единственный корень.

Ответ: при р ≠ 5 x = 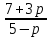; при р = 5 корней нет.

Мы нашли зависимость решения уравнения от параметра. Если решаем уравнения, содержащие параметры, мы можем сказать, при каких значениях параметра уравнение имеет единственное решение, когда решений бесконечное множество, а в каких случаях их нет вообще.

Пример 2. Решим уравнение относительно переменной x:

x =

Это выражение имеет смысл при любых значениях c и b поэтому уравнение имеет единственное решение.

Ответ: x =

Пример 3. Решим уравнение относительно переменной y:

Если b = 3 и 2 – 2a ≠ 0 (a ≠ 1), то корней нет, т.к. получим равенство, которое не выполняется ни при каких значениях переменной.

Если b = 3 и a = 1, то получим 0  y = 0. Уравнение имеет бесконечное множество решений.

Если b ≠ 3, то y = 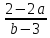– единственный корень.

Ответ: при b ≠ 3 y = 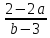; при b = 3 и a = 1 – бесконечно много решений; при b = 3 и a ≠ 1 – корней нет.

Источник

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

при а = 1 х – любое действительное число, кроме х = 1

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Источник

Урок по алгебре в 7,8 классе «Линейное уравнение с параметром и его решение в общем виде»

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Тема: Линейное уравнение с параметром и его решение в общем виде.

Образовательные: дать определение линейного уравнения с параметром, рассмотреть способы его решения, схему исследования линейных уравнений с параметрами. Формировать навыки решения линейных уравнений с параметрами.

Развивающие: развивать уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.

Воспитательные: формирование волевые качества, формирование коммуникабельность, выработка объективной оценки своих достижений, формирование ответственности.

Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.

ученики записывают на доске решения уравнений;

обсуждение, замечания, уточнения к решениям на доске.

Если m = 0, то уравнение примет вид 0 • m = 6 и не имеет решений;

Если m ≠ 0, то уравнение примет вид х = и имеет единственное решение.

Ответ: при m = 0 нет решений; при m ≠ 0 х = .

№ 2. При каком значении b уравнение |х| + b = 0 не будет иметь корней?

Если b = 0, то уравнение примет вид |х| = 0, т.е. х = 0 и имеет ед. решение;

Если b > 0, то уравнение не имеет решений;

1. Определение линейного уравнения с параметром.

Уравнение вида Ах = В, (1)

называется линейным уравнением с параметрами.

2. что значит решить уравнение с параметрами?

в) способы решения линейного уравнения.

Линейные уравнения с параметром решаются двумя способами: аналитическим и графическим.

Графический способ решения линейного уравнений с параметром удобен тогда, когда нужно определить количество корней уравнения.

Аналитический способ решения линейного уравнения с параметром удобен тогда, когда требуется найти решение уравнения при каждом значении параметра.

г) схема исследования линейного уравнения (1).

Замечание. Если линейное уравнение не представлено в виде (1), то сначала нужно привести его к виду (1) и только после этого проводить исследование.

№ 1. Решить уравнение: а) (а + 3)х =5.

Ответ: при а = 6 нет решений; при а ≠ 6 х = .

№ 2. Решить уравнение: а) (а + 4)х = 2а +1.

№ 3. Решить уравнение: а) (а + 1)х = а + 1.

Если а – 4 = 0, т.е. а = 4, то уравнение примет вид 0 • х = 0 и имеет бесконечное

№ 4. Решить уравнение: а) (а – 7)х = а(а – 7).

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное

№ 5. Решить уравнение (а – 7)х = а 2 – 14а + 49.

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное

Что нового сегодня Вы узнали на уроке? Дайте определение линейного уравнения с параметрами. Что значит решить уравнение с параметром? Назовите способы решения и схему исследования линейного уравнения с параметром.

Решить уравнения: а) (а – 9)х = 4; б) (а – 6)х = а + 8; в) (а + 3)х = а + 3;

г) (а + 2)х = (а + 2)(а – 3); г) (а + 3)х = а 2 + 6а + 9.

Источник

Презентация по алгебре на тему: «Линейные уравнения с параметром»(7 класс)

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Описание презентации по отдельным слайдам:

Линейные уравнения с параметром. Г.Новосибирск Учитель высшей квалификационной категории Баринова Людмила Леонидовна

Содержание Цель Знакомство параметром Решение простейших линейных уравнений с параметром Алгоритм решения линейных уравнений с параметром. Список литературы

Цель Цель моей работы заключается в том, чтобы познакомится с понятием параметра и научиться решать простейшие уравнения с параметром.

Знакомство с параметром Параметр – независимая переменная, значение которой в задаче считается заданным фиксированным число или произвольным действительным числом Решить уравнение с параметром – значит, для любых допустимых значений параметра найти значения неизвестной переменной.

При каких значениях a и в уравнение ax = в имеет решения не имеет корней 0х=в (Ответ: при a = 0, в ≠0) имеет бесконечно много корней 0х=0 (Ответ: при а=0,в=0) имеет единственный корень (Ответ: при а ≠0)

При каких значениях a уравнение ax = 2a – 1 не имеет корней (Ответ: при a = 0) имеет бесконечно много корней (Ответ: таких значений a нет) имеет единственный корень (Ответ: при а ≠0) Х=2а-1/а

Решение простейших линейных уравнений с параметром. Рассмотрим линейное уравнение х+а=ах+1 ☺ где а – параметр. х-ах=1-а х(1-а) =1-а Ответ. Если а=1, то х e R Если а≠1, то х=1

Уравнение № 2 n2x + 3nx = 5n + 15. Решение: n2x + 3nx = 5n + 15; n (n + 3) x = 5 (n + 3); n = – 3; 0 – контрольные значения параметра

уравнение №3 a2x – 2a = a2 + ax; a2x – ax = a2 + 2a; a(a – 1)x = a (a + 2); a(a – 1) = 0, a = 0; 1 – контрольные значения параметра

уравнение №4 = ; 2 mx – 4 = 3 – mx; 2 mx + mx = 3 + 4; 3 mx = 7; m = 0 – контрольное значение параметра.

Алгоритм решения линейных уравнений с параметром аналитическим способом 1.Привести уравнение к виду ах=в. 2.Найти контрольные значения параметра а. 3.Подставить контрольные значения в уравнение ах=в и выяснить сколько решений имеет уравнение. 4.Записать при каких значениях параметра а уравнение имеет единственное решение. 5. Записать правильно ответ.

Для тех, кто хочет знать больше. 1. При каких a уравнение 6(ax-1)-a=2(a+x)-7 имеет бесконечно много решений? 2. При каких a уравнение 2(a-2x)=ax+3 не имеет решений? 3. При каком a прямые 2x+2y=4 и ax-5y=13 пересекаются в точке, принадлежащей оси абсцисс? 4. При каком a прямые 7x-9y=14 и 6x-ay=10 пересекаются в точке, принадлежащей оси ординат? 5. При каком a уравнение 3(x-2a)=4(1-x) имеет отрицательное решение?

Спасибо за внимание!

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Номер материала: ДВ-246820

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В России разработали программу содействия занятости молодежи до 2030 года

Время чтения: 1 минута

ЕГЭ в 2022 году может пройти в допандемийном формате

Время чтения: 1 минута

Школы организуют экскурсии и спортивные игры в день выборов

Время чтения: 1 минута

ВПР начались в колледжах с 15 сентября

Время чтения: 4 минуты

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

Игры со взрослыми полезнее для развития детей, чем игры со сверстниками

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

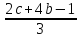
Источник