Какие параметры однозначно характеризуют земной эллипсоид
Геодезия
Для студентов аспирантов и преподавателей
Разделы
Общий земной эллипсоид
При изучении фигуры Земли с давних пор поступают следующим образом. Сначала определяют форму и размеры некоторой модели Земли, поверхность которой сравнительно проста, хорошо изучена в геометрическом отношении, удобна для решения на ней разнообразных задач геодезии и картографии и наиболее полно характеризует в первом приближении форму и размеры реальной Земли. Затем, приняв поверхность этой модели Земли за отсчетную, определяют относительно нее высоты точек поверхности изучаемой фигуры — геоида (квазигеоида) или реальной Земли — и таким образом получают данные, характеризующие форму и размеры конкретной фигуры.
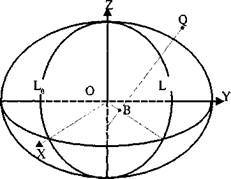
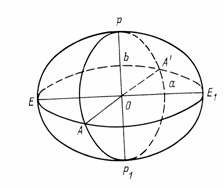
При решении задач высшей геодезии за такую модель Земли принимают эллипсоид вращения с малым полярным сжатием, называемый общим земным эллипсоидом (рис. 4). Его поверхность может быть получена вращением полуэллипса РЕР1 вокруг его малой оси РР1.
Форма и размеры земного эллипсоида характеризуются большой а и малой bполуосями, а чаще большой полуосью а и полярным сжатием а,
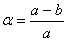
или большой полуосью а и первым эксцентриситетом е меридианного эллипса:
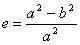
Для того чтобы общий земной эллипсоид возможно точнее характеризовал форму и размеры всей Земли, его параметры а, а определяют с учетом следующих условий:
1) центр общего земного эллипсоида должен совпадать с центром масс Земли, а его малая ось — с осью вращения Земли;
2) объем эллипсоида должен быть равен объему геоида (квазигеоида);
3) сумма квадратов отклонений по высоте поверхности эллипсоида от поверхности геоида (квазигеоида) должна быть наименьшей.
До недавнего времени, т. е. до начала освоения человеком космического пространства, параметры земного эллипсоида получали, выполняя так называемые градусные измерения. С этой целью прокладывали ряды триангуляции по направлению меридианов и параллелей на разных широтах, на конечных пунктах которых определяли астрономические широты, долготы, а также азимуты сторон. Для вывода надежных значений параметров общего земного эллипсоида градусные измерения, в принципе, необходимо было выполнить на всей поверхности Земли, включая Мировой океан. Кроме того, астрономические широты, долготы и азимуты следовало исправить поправками за влияние уклонений отвесных линий, которые, как правило, были неизвестны.
В прошлом градусные измерения велись только на материках, т. е. на незначительной части земной поверхности. Градусные измерения разных стран не имели общих связей, выполнялись по разным программам с разной точностью, обрабатывались в разных системах координат. Все это затрудняло их совместное использование и отрицательно сказывалось на точности выводов размеров земного эллипсоида.
В течение полутора веков ученые многих стран занимались определением размеров земного эллипсоида, используя имеющиеся в разном объеме разной точности и содержания градусные измерения. Приведем некоторые результаты таких определений (табл.» 1).
Эллипсоид Деламбра имеет только лишь историческое значение как основа для установления метрической системы мер. На поверхности эллипсоида Деламбра расстояние от полюса до экватора точно составляет 10000 км, так как в то время 1 м
Земной эллипсоид
Земной эллипсоид — эллипсоид вращения, размеры которого подбираются при условии наилучшего соответствия фигуре квазигеоида для Земли в целом (общеземной эллипсоид) или отдельных её частей (референц-эллипсоид).
Содержание
Параметры земного эллипсоида
Земной эллипсоид имеет три основных параметра, любые два из которых однозначно определяют его фигуру:
Существуют также и другие параметры эллипсоида:
Для практической реализации земной эллипсоид необходимо ориентировать в теле Земли. При этом выдвигается общее условие: ориентирование должно быть выполнено таким образом, чтобы разности астрономических и геодезических координат были минимальными.
Референц-эллипсоид
Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимаются для обработки геодезических измерений законодательно. В России/CCCР с 1946 года используется эллипсоид Красовского.
Ориентирование референц-эллипсоида в теле Земли подчиняется следующим требованиям:
Для закрепления референц-эллипсоида в теле Земли необходимо задать геодезические координаты B0, L0, H0 начального пункта геодезической сети и начальный азимут A0 на соседний пункт. Совокупность этих величин называется исходными геодезическими датами.
Основные референц-эллипсоиды и их параметры
| Учёный | Год | Страна | a, м | 1/f |
|---|---|---|---|---|
| Деламбр | 1800 | Франция | 6 375 653 | 334,0 |
| Деламбр | 1810 | Франция | 6 376 985 | 308,6465 |
| Вальбек | 1819 | Финляндия,Российская Империя | 6 376 896 | 302,8 |
| Airy | 1830 | 6 377 563,4 | 299.324 964 6 | |
| Эверест | 1830 | Индия, Пакистан, Непал, Шри-Ланка | 6 377 276,345 | 300.801 7 |
| Бессель | 1841 | Германия, Россия (до 1942 г.) | 6 377 397,155 | 299.152 815 4 |
| Теннер | 1844 | Россия | 6 377 096 | 302.5 |
| Кларк | 1866 | США, Канада, Лат. и Центр. Америка | 6 378 206,4 | 294.978 698 2 |
| Кларк | 1880 | Франция, ЮАР | 6 377 365 | 289.0 |
| Листинг | 1880 | 6 378 249 | 293.5 | |
| Гельмерт | 1907 | 6 378 200 | 298,3 | |
| Хейфорд | 1910 | Европа, Азия, Ю.Америка, Антарктида | 6 378 388 | 297,0 |
| Хейсканен | 1929 | 6 378 400 | 298,2 | |
| Красовский | 1936 | СССР | 6 378 210 | 298,6 |
| Красовский | 1940 | СССР,Россия, страны СНГ, вост. Евр, Антарктида | 6 378 245 | 298.299 738 1 |
| Эверест | 1956 | Индия, Непал | 6 377 301,243 | 300.801 7 |
| IAG-67 | 1967 | 6 378 160 | 298.247 167 | |
| WGS-72 | 1972 | 6 378 135 | 298.26 | |
| IAU-76 | 1976 | 6 378 140 | 298.257 | |
| ПЗ-90 | 1990 | Россия | 6 378 136 | 298.258 |
Общеземной эллипсоид
Общеземной эллипсоид должен быть ориентирован в теле Земли согласно следующим требованиям:
При ориентировании общеземного эллипсоида в теле Земли (в отличие от референц-эллипсоида) нет необходимости вводить исходные геодезические даты.
Поскольку требования к общеземным эллипсоидам на практике удовлетворяются с некоторыми допусками, а выполнение последнего (3) в полном объеме невозможно, то в геодезии и смежных науках могут использоваться различные реализации эллипсоида, параметры которых очень близки, но не совпадают (см. ниже).
Современные общеземные эллипсоиды и их параметры
| Название | Год | Страна/организация | a, м | точность ma, м | 1/f | точность mf | Примечание |
|---|---|---|---|---|---|---|---|
| GRS80 | 1980 | МАГГ (IUGG) | 6 378 137 | ± 2 | 298,257 222 101 | ± 0,001 | (англ. Geodetic Reference System 1980) разработан Международной Ассоциацией Геодезии и Геофизики (англ. International Union of Geodesy and Geophysics ) и рекомендован для геодезических работ |
| WGS84 | 1984 | США | 6 378 137 | ± 2 | 298,257 223 563 | ± 0,001 | (англ. World Geodetic System 1984) применяется в системе спутниковой навигации GPS |
| ПЗ-90 | 1990 | СССР | 6 378 136 | ± 1 | 298,257 839 303 | ± 0,001 | (Параметры Земли 1990 года) используется на территории России для геодезического обеспечения орбитальных полетов. Этот эллипсоид применяется в системе спутниковой навигации ГЛОНАСС |
| МСВЗ (IERS) | 1996 | IERS | 6 378 136,49 | — | 298,256 45 | — | (англ. International Earth Rotation Service 1996 ) рекомендован Международной службой вращения Земли для обработки РСДБ-наблюдений |
См. также
Ссылки
Смотреть что такое «Земной эллипсоид» в других словарях:
ЗЕМНОЙ ЭЛЛИПСОИД — эллипсоид вращения, наиболее близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений искусственного спутника Земли. В Российской Федерации, ряде стран Вост.… … Большой Энциклопедический словарь
земной эллипсоид — Эллипсоид, который характеризует фигуру и размеры Земли. [ГОСТ 22268 76] [ГОСТ Р 52334 2005 ] Тематики геодезиягравиразведка и магниторазведка Обобщающие термины фигура земли EN Earth ellipsoid DE Erdellipsoid FR ellipsoide terrestre … Справочник технического переводчика
Земной эллипсоид — означает математическую модель поверхности Земли. Стандарт для этой модели будет согласован Сторонами. Источник: МЕМОРАНДУМ О ПОНИМАНИИ ОБ УВЕДОМЛЕНИЯХ О ПУСКАХ РАКЕТ … Официальная терминология
земной эллипсоид — Форма планеты Земля, выраженная через ее эллиптичность, т.е. сжатие Земли (принятый стандарт земного эллипсоида: R=6378160 м, r=6356775 м, сплюснутость = 0,003353) … Словарь по географии
Земной эллипсоид — 14. Земной эллипсоид D. Erdellipsoid E. Earth ellipsoid F. Ellipsoide terrestre Эллипсоид, который характеризует фигуру и размеры Земли Источник: ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа земной эллипсоид Эллипсоид,… … Словарь-справочник терминов нормативно-технической документации
земной эллипсоид — эллипсоид вращения, наиболее близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений ИСЗ. В России, ряде стран Восточной Европы и др. принят Красовского… … Энциклопедический словарь
Земной эллипсоид — Эллипсоид вращения, наилучшим образом представляющий фигуру Геоида, т. е. фигуру Земли в целом. Для наилучшего представления геоида в пределах всей Земли обычно вводят общий З. э. и определяют его так, чтобы: 1) объём его был равен объёму … Большая советская энциклопедия
ЗЕМНОЙ ЭЛЛИПСОИД — эллипсоид вращения, наиб. близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений ИСЗ. В России, ряде стран Вост. Европы и др. принят Красовского эллипсоид.… … Естествознание. Энциклопедический словарь
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
Эллипсоид Бесселя — Эллипсоид Бесселя земной эллипсоид, определённый из измерений в 1841 году Фридрихом Бесселем. В Европе он используется в таких страна как: в Германии, Австрии, Швейцарии, Чехии и странах бывшей Югославии. также используется в Индонезии,… … Википедия
Земной эллипсоид
Смотреть что такое «Земной эллипсоид» в других словарях:
Земной эллипсоид — эллипсоид вращения, размеры которого подбираются при условии наилучшего соответствия фигуре квазигеоида для Земли в целом (общеземной эллипсоид) или отдельных её частей (референц эллипсоид). Содержание 1 Параметры земного эллипсоида 2 … Википедия
ЗЕМНОЙ ЭЛЛИПСОИД — эллипсоид вращения, наиболее близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений искусственного спутника Земли. В Российской Федерации, ряде стран Вост.… … Большой Энциклопедический словарь
земной эллипсоид — Эллипсоид, который характеризует фигуру и размеры Земли. [ГОСТ 22268 76] [ГОСТ Р 52334 2005 ] Тематики геодезиягравиразведка и магниторазведка Обобщающие термины фигура земли EN Earth ellipsoid DE Erdellipsoid FR ellipsoide terrestre … Справочник технического переводчика
Земной эллипсоид — означает математическую модель поверхности Земли. Стандарт для этой модели будет согласован Сторонами. Источник: МЕМОРАНДУМ О ПОНИМАНИИ ОБ УВЕДОМЛЕНИЯХ О ПУСКАХ РАКЕТ … Официальная терминология
земной эллипсоид — Форма планеты Земля, выраженная через ее эллиптичность, т.е. сжатие Земли (принятый стандарт земного эллипсоида: R=6378160 м, r=6356775 м, сплюснутость = 0,003353) … Словарь по географии
Земной эллипсоид — 14. Земной эллипсоид D. Erdellipsoid E. Earth ellipsoid F. Ellipsoide terrestre Эллипсоид, который характеризует фигуру и размеры Земли Источник: ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа земной эллипсоид Эллипсоид,… … Словарь-справочник терминов нормативно-технической документации
земной эллипсоид — эллипсоид вращения, наиболее близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений ИСЗ. В России, ряде стран Восточной Европы и др. принят Красовского… … Энциклопедический словарь
ЗЕМНОЙ ЭЛЛИПСОИД — эллипсоид вращения, наиб. близкий к фигуре геоида; его размеры и положение в теле Земли определяют из градусных измерений, измерений ускорения силы тяжести и наблюдений ИСЗ. В России, ряде стран Вост. Европы и др. принят Красовского эллипсоид.… … Естествознание. Энциклопедический словарь
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
Эллипсоид Бесселя — Эллипсоид Бесселя земной эллипсоид, определённый из измерений в 1841 году Фридрихом Бесселем. В Европе он используется в таких страна как: в Германии, Австрии, Швейцарии, Чехии и странах бывшей Югославии. также используется в Индонезии,… … Википедия
Земной эллипсоид



Известно, что Земля шарообразна и по форме близка к сфероиду — фигуре, которую она приняла бы под влиянием только сил взаимного тяготения и центробежной силы вращения вокруг полярной оси. Из-за неравномерного распределения масс Земля имеет обширные, хотя и довольно пологие, выпуклости и вогнутости.
Фигуру Земли можно представить, вообразив поверхность, в каждой точке которой сила тяжести направлена по нормали к ней, т.е. по отвесной линии. Такую поверхность называют уровенной. Сложную фигуру нашей планеты, ограниченную уровенной поверхностью, проходящей через точку, закрепленную на высоте среднего уровня моря и являющуюся началом отсчета высот, называют геоидом. Иначе говоря, геоид представляет фигуру Земли, сглаженную до уровня Мирового океана (рис. 3.1). Благодаря использованию искусственных спутников и наземных измерений геоид достаточно изучен. При картографировании сложную фигуру геоида заменяют математически более простой — эллипсоидом вращения — геометрическим телом, которое образуется при вращении эллипса вокруг его малой оси (рис. 3.2). Наиболее известные эллипсоиды представлены в табл. 3.1.
В нашей стране в 1940 г. расчет эллипсоида был выполнен выдающимся ученым Ф. Н. Красовским (1878—1948) и его учеником А. А. Изотовым (1907—1988). Эллипсоид Красовского был утвержден в СССР для геодезических и картографических работ, его используют в России и в настоящее время.
Параметры эллипсоида, рекомендованные в 60-х годах международными астрономо-геодезическими организациями, применялись в Австралии, прилегающих к ней странах и в Южной Америке. Эллипсоиды системы геодезических параметров GRS-67
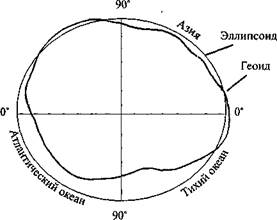 |
| Северный Ледовитый океан |
| Антарктида |
| Рис. 3.1. Меридиональное сечение геоида и земного эллипсоида |
Рис. 3.2. Эллипсоид вращения (В, L — широта и долгота точки Q; L0 — начальный меридиан)
По табл. 3.1 нетрудно проследить, как со временем повышалась точность определения большой полуоси и сжатия земного эллипсоида. В настоящее время параметры современной точности имеют эллипсоид системы GRS-80
Таблица 3.1 Основные земные эллипсоиды и их параметры
| Эллипсоид | Годы | Большая полуось а (м) | Сжатие а |
| Дсламбра | 6 375 653 | 1/334 | |
| Вальбека | 6 376 896 | 1/303 | |
| )йри | 6 377 563,396 | 1/299,3249646 | |
| ‘•) нереста | 6 377 276,345 | 1/300,8017 | |
| Ьссселя | 6 377 397 | 1/299,15 | |
| Кларка | 6 378 206 | 1/294,98 | |
| Кларка | 6 378 249 | 1/293,46 | |
| Хейфорда | 6 378 388 | 1/297 | |
| Красовского | 6 378 245 | 1/298,3 | |
| Австралийский | 6 378 160 _j | 1/298,25 | |
| GRS-67 | 6 378 160 | 1/298.247167247 | |
| WGS-72 | 6 378 135 | 1/298,26 | |
| GRS-80 | 6 378 137 | 1/298,257222101 | |
| WGS-84 | 6 378 137 | 1/298,257223563 | |
| ПЗ-90 | 6 378 136 | 1/298,257839303 |
Австралии, Европы, стран Северной и Центральной Америки, WGS-84 (WorldGeodeticSystem, 1984), получивший мировое распространение благодаря американской глобальной системе спутникового позиционирования, и российский ПЗ-90 (Параметры Земли, 1990).
Различают общеземной эллипсоид,наилучшим образом подходящий для решения глобальных картографо-геодезических задач, и конференц-эллипсоиды, используемые в отдельных регионах и странах.
Эллипсоид вращения характеризуют два параметра: большая экваториальная полуось (а) и полярное сжатие.
Эти параметры, а также площади поверхностей для эллипсоидов WGS-84, ПЗ-90 и Красовского, наиболее важных для картографических и геодезических работ в России, приведены в табл. 3.2.
Параметрыосновных земных эллипсоидов
| Параметры | Эллипсоиды | ||
| WGS-84 | ПЗ-90 | Красовского | |
| а | 6 378 137 | 6 378 136 | 6 378 245 |
| b | 6 356 752,314 | 6 356 751,362 | 6 356 863,019 |
| а | 1/298,257223563 | 1/298,257839303 | 1/298,3 |
| е 2 | 0,006694379990 | 0,006694366193 | 0,006693421623 |
| Площадь | 510 065 622 | 510 065 464 | 510 083 059 |
Положение любой точки на земном эллипсоиде определяется широтой и долготой.
Широта (В) — угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью его экватора; долгота (L) — двугранный угол между плоскостями меридианов данной точки и начального меридиана (см. рис. 3.2).
Рассекая эллипсоид плоскостями, проходящими через полярную ось, получают линии меридианов, а плоскостями, проходящими перпендикулярно этой оси, — линии параллелей. Линия экватора — след сечения эллипсоида плоскостью, проходящей через его центр перпендикулярно полярной оси.
Сетка меридианов и параллелей на земном эллипсоиде, шаре или на глобусе называется географической сеткой.
Наиболее важными радиусами эллипсоида вращения являются:
М — радиус кривизны меридиана;
N — радиус кривизны первого вертикала (линии, получаемой сечением эллипсоида плоскостью, проходящей через нормаль в данной точке и перпендикулярно плоскости меридиана);
R— средний из радиусов всевозможных сечений, проведенных через нормаль в данной точке эллипсоида;
г — радиус параллели.
Легко заметить, что радиус М у полюса больше, чем на экваторе. Это означает, что кривизна меридианного эллипса убывает от экватора к полюсам. Радиус меридиана получает наибольшие изменения на средней широте, где с каждым градусом широты он изменяется примерно на 1 км. Радиус М нужен прежде всего для вычисления длин дуг меридианов и нахождения широт по этим дугам. Средний радиус кривизны Rприменяют, например, в задачах, связанных с развертыванием поверхности эллипсоида на поверхность сферы. В табл. 3.3 приведены значения радиусов эллипсоида на разных широтах и диапазоны их изменения.
Таблица 3.3 Радиусы земного эллипсоида на разных широтах
При создании и использовании карт приходится определять длины дуг параллелей и меридианов. Наиболее просто вычисляется длина дуги параллели. Параллель — окружность, ее длина Spмежду двумя точками с долготами Lxи L2равна произведению радиуса этой параллели на разность долгот, выраженных в радианной мере. Меридиан — эллипс. Вычисления его длин дуг более сложны.
Какие параметры однозначно характеризуют земной эллипсоид
Установить точное положение геоида под материками невероятно сложно, так как для математического выражения геоида используются коэффициенты сферических гармоник. Например, некоторые геоиды использует коэффициенты сферических гармоник для полиномов до 360 порядка и для полного уравнения требуется более 60 000 коэффициентов. Для расчета поверхности это все слишком сложно. Поэтому используется более простая фигура, но с достаточной точностью описывающая землю.
Для упрощения математических расчетов используется более удобный двухосный эллипсоид вращения, при этом он не сильно отличается от формы земли. Поверхности эллипсоида и геоида отличаются в пределах 100 метров в ту или иную сторону.
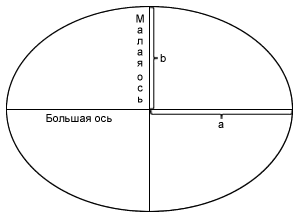
Форма эллипса определяется двумя радиусами. Более длинный радиус называется большой полуосью (как правило обозначается буквой a), а меньший (короткий)- малой полуосью (как правило обозначается буквой b).
Рисунок 26. Эллипсоид
Эллипсоид вращения, который наилучшим образом согласуется с поверхностью геоида называют общеземной эллипсоид или эллипсоид земли.
Эллипсоид, который наилучшим образом согласуется с геоидом на ограниченной части его поверхности называется референц-эллипсоид (от лат. referens – вспомогательный).
Эллипсоид вращения может быть определен либо большой полуосью, a, и малой полуосью, b, либо величиной a и сжатием.
Сжатие разность в длине между двумя осями, выраженная простой или десятичной дробью:
Сжатие является маленькой величиной, поэтому как правило вместо него используется величина 1/f.
Далее представлены некоторые референц-эллипсоиды и их параметры:
Помимо эллипсоида в геодезии используется такое понятие как датум. Датум (лат. Datum) — набор параметров, используемых для смещения и трансформации референц-эллипсоида в локальные географические координаты. Понятие датум используется в геодезии и картографии для наилучшей аппроксимации к геоиду в данном месте.
Датум задается смещением референц-эллипсоида по осям: X, Y, Z, а также поворотом декартовой системы координат в плоскости осей на угол rX, rY, rZ. Также необходимо знать параметры референц-эллипсоида а и f, где а — размер большой полуоси, f — сжатие эллипсоида.
Существуют два типа датумов- геоцентрический (глобальный) и локальный. Геоцентрический датум использует центр масс земли в качестве начала отсчета. Начало отсчета системы координат для локального датума сдвинуто относительно центра земли. Локальный датум изменяет положение эллипсоида так, чтобы наиболее близко совместить его поверхность с нужной областью. Локальный датум не следует применять вне области, для которой он был разработан.
Наиболее широко используемым датумом является Мировая геодезическая система 1984 года (World Geodetic System 1984- WGS84), базируется он на эллипсоиде WGS-84 с центром в центре масс земли. Так же один из достаточно распространенных датумов (используется в России и некоторых окружающих странах) является- Pulkovo-1942 (СК-42), который базируется на эллипсоиде Крассовского, начало координат у него смещено относительно центра масс расстояние около 100 м.
Система WGS-84 широко применяется за рубежом, ее используют практически для всех данных производимых в мире, так же она используется практически во всех навигаторах. СК-42 широко используется в российской картографии, на ней основываются все топографические материалы ВТУ ГШ РФ (Военно-топографического управления Генерального штаба Российской Федерации).
Далее представлены некоторые датумы:
Поддерживаемые ZuluGIS датумы приведены в приложении: Таблица 16, «Датумы».