Критические параметры уравнения ван дер ваальса
Изотермы Ван-дер-Ваальса. Связь критических параметров с постоянными в уравнении Ван-дер-Ваальса
Законы идеального газа являются приближенными, а отступления от этих законов обусловлены существенным отличием свойств идеального и реального газов. В отличие от идеального газа между молекулами реального газа существуют силы взаимодействия, которые на малых расстояниях между молекулами носят характер отталкивания, а на достаточно больших расстояниях между молекулами действуют силы притяжения. Кроме этого, молекулы реального газа не могут быть представлены как материальные точки. Молекулы реального газа имеют отличный от нуля собственный объем. Учет собственного объема и сил взаимодействия позволил получить уравнение состояния для реального газа.
, (1)
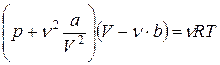
Теоретически полученное уравнение (1) называется уравнением Ван-дер-Ваальса.
Рассмотрим экспериментальные изотермы жидкости, пара и перехода жидкость – пар. На рисунке 1 показан теоретический график зависимости давления от объема для реального газа, который строится на основе анализа уравнения Ван-дер-Ваальса при помощи компьютерной модели.
Между поправками уравнения Ван-дер-Ваальса a и b, критическим давлением pкр, критической температурой Tкр и критическим молярным объемом Vкр0 в критическом состоянии существует следующая связь:
, 
, 
. (2)
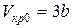
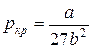
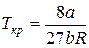
Действительно, в точке перегиба К критической изотермы первая и вторая производные от давления по объему равны нулю, т.е.
и 
. (3)
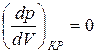
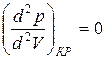
Для доказательства соотношений 2 проанализируем уравнение Ван-дер-Ваальса для одного моля газа.
. (4)
Из уравнения (4) определим давление.
. (5)
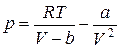
Далее найдем первую и вторую производные от давления по объему и приравняем полученные значения для критического состояния к нулю.
. (6)
. (7)
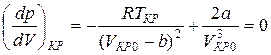
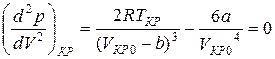
Из уравнений (6) и (7) получим:
. (8)
. (9)
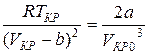
Разделив почленно соотношения (8) на (9), найдем критический объем:
.
. (10)
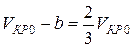
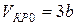
Подставляя уравнение (10) в соотношение (8), определим критическую температуру:
. (11)
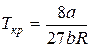
И, наконец, подставляя соотношения (10) и (11) в уравнение (5) для критического состояния, найдем критическое давление:
. (12)
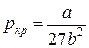
2.5. Уравнение Ван-дер-Ваальса
Уравнение Клапейрона — Менделеева следует из молекулярно-кинетической теории в предположении идеальности газа. Если мы хотим описывать поведение реальных систем, надо учесть взаимодействие молекул между собой. Точный учет межмолекулярных сил — задача чрезвычайно трудная. Поэтому было предложено несколько модификаций уравнения состояния идеального газа, которые могли бы учесть основные особенности реальных систем. Наиболее удачной попыткой стало уравнение Ван-дер-Ваальса, при получении которого вносились поправки в уравнение состояния идеального газа
В подходе Ван-дер-Ваальса, во-первых, принимается во внимание, что молекулы имеют конечные размеры. Если обозначить собственный объем всех молекул в моле вещества буквой b, то для движения молекул остается свободный объем
и именно он должен фигурировать в уравнении состояния. Во-вторых, учитывается, что молекула, подлетающая к стенке сосуда, «чувствует» притяжение других молекул, которое уравновешивалось, когда молекула была внутри сосуда. Дополнительная сила, направленная внутрь сосуда, эквивалентна дополнительному давлению pi, (его называют «внутренним» давлением газа). Поэтому вместо давления р газа на стенки сосуда уравнение состояния должно содержать сумму р+рi.
Как зависит внутреннее давление pi от параметров системы? Сила, действующая на каждую молекулу, пропорциональна концентрации п молекул в системе. Число подлетающих к стенке молекул также пропорционально п, и потому внутреннее давление пропорционально квадрату концентрации частиц:
Обозначая коэффициент пропорциональности буквой а, приходим к уравнению Ван-дер-Ваальса
Для одного моля вещества это уравнение упрощается:
Критические параметры уравнения ван дер ваальса
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).
Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)
постоянная b учитывает собственный мольный объем молекул.
При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления 
(иногда его называют статическим давлением). Изначально величина была учтена в общей форме в уравнении Гирна (1865)
(p + ) (V – nb) = nRT. (1.4)
Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
(1.5)
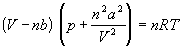
или для одного моля
. (1.6)
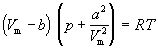
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.
Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов
Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление
(1.7)
(1.8)
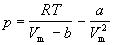
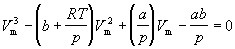
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.
На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы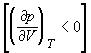 
. Состояния на участках 12 и 54, которые соответствуют переохлажденному пару и перегретой жидкости, соответственно, являются неустойчивыми (метастабильными) и могут быть лишь частично реализуемы в специальных условиях. Так, осторожно сжимая пар выше точки 1 (рис. 1.4), можно подняться по кривой 12. Для этого необходимо отсутствие в паре центров конденсации, и в первую очередь пыли. В этом случае пар оказывается в пересыщенном, т.е. переохлажденном состоянии. И наоборот, образованию капелек жидкости в таком паре способствуют, например, попадающие в него ионы. Это свойство пересыщенного пара используется в известной камере Вильсона (1912), применяемой для регистрации заряженных частиц. Движущаяся заряженная частица, попадая в камеру, содержащую пересыщенный пар, и соударяясь с молекулами, образует на своем пути ионы, создающие туманный след – трек, который фиксируется фотографически.
Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.
По мере повышения температуры все три корня сближаются, и при критической температуре Tc все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [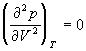
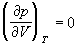
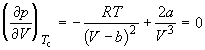
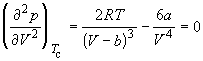
] с горизонтальной касательной [
], то есть
, (1.9)
. (1.10)
Совместное решение этих уравнений дает:
, (1.11)
, (1.12)
, (1.13)
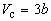
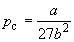
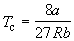
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Zc для всех газов должен быть равен
(1.14)
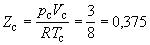
Из таблицы 1.2 видно, что хотя значение Zc для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;
2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);
3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).
Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).
Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Уравнение Ван-дер-Ваальса
При низких давлениях и высоких температурах закон Менделеева-Клапейрона также довольно точно описывает поведение реальных газов, однако в других условиях реальные газы значительно отклоняются от идеальности. Уравнение Ван-дер-Ваальса учитывает эти отклонения.
Формула уравнения Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса имеет вид:
В этом уравнении n – количество молей газа, р – его давление, V – занимаемый газом объем, Т – абсолютна температура газа. Универсальная газовая постоянная имеет значение 8,31441 Дж/(моль•К), одинаковое для всех газов.
Переменная а – это поправка на силу притяжения между молекулами газа. Под действием этой силы молекулы притягиваются друг к другу, внутрь газа, уменьшая давление на стенку. Переменная b – поправка, учитывающая собственный объем, занимаемый молекулами газа. Эти поправки зависят от вида газа, и могут быть найдены из таблиц либо рассчитаны по следующим формулам:
Здесь 
и 
– это давление и абсолютная температура газа в критической точке, то есть в точке перехода газообразной фазы в жидкую.
В реальном газе расстояния между молекулами меньше, чем в идеальном, и сравнимы с размерами самих молекул. Поэтому силы взаимодействия между молекулами становятся достаточно большими. В объеме газа молекула со всех сторон окружена другими молекулами, и силы их притяжения уравновешиваются. Однако когда молекула приближается к стенке, силы притяжения больше не уравновешиваются и «втягивают» её внутрь. Поэтому молекула движется к стенке медленнее, из-за чего давление на стенку уменьшается. Это и учитывает поправка а.
Кроме того, за счёт сил межмолекулярного взаимодействия реальные газы способны переходить в жидкое состояние, и уравнение Ван-дер-Ваальса довольно точно описывает поведение газов вблизи этого перехода.
Так как в реальном газе расстояние между молекулами сравнительно невелико, молекула должна пролететь меньшее расстояние, чтобы удариться о стенку. Поэтому при очень больших давлениях давление на стенку возрастает, и это учитывает поправка b.
Уравнение Ван-дер-Ваальса применяется, в частности, при определении параметров пара в теплотехнике и теплотехнике, при исследовании сжижения газов.
Примеры решения задач
| Задание | Какую температуру имеет азот массой 2 грамма, занимающий объём 800 см  при давлении 0,2 МПа, если его рассматривать как реальный газ? |
| Решение | Для удобства переведем значения величин в систему СИ: |
800 см 3 = 0,0008 м 3 ;
Табличные значения поправок a и b для азота:
a = 0,136 Па•м 6 /моль 2 ;
Определим, сколько молей содержится в 4 г водорода. Учтём, что водород – двухатомный газ, поэтому его молекулярная масса М – сумма двух атомных масс водорода А.
=0,071 моль.
Выразим температуру из уравнения Ван-дер-Ваальса:
| Задание | Вычислить поправки a и b в уравнении Ван-дер-Ваальса для азота, если известны критическая температура Ткр = 126 К и критическое давление ркр = 3,39 МПа. |
и разделив на p, получим кубическое уравнение относительно объема:
Это уравнение имеет три корня. В точке перегиба, показанной на рисунке, все эти корни действительны и равны друг другу. Точка перегиба и есть критической точкой, в которой газообразная фаза переходит в жидкую.
Чтобы найти критические параметры, воспользуемся свойствами точки перегиба: первая и вторая производная уравнения обращаются в нуль.
Решим эти уравнения относительно объема и температуры, получим критические параметры:
Выразив давление из уравнения Ван-дер-Ваальса и записав это уравнение для критических параметров, получим:
Подставим в это уравнение 
, и после решения получим:
Запишем систему уравнений:
м 3 /моль.
Подставив b во второе уравнение системы, получим:
Критические параметры уравнения ван дер ваальса
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).
Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)
постоянная b учитывает собственный мольный объем молекул.
При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления 
(иногда его называют статическим давлением). Изначально величина была учтена в общей форме в уравнении Гирна (1865)
(p + ) (V – nb) = nRT. (1.4)
Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
(1.5)
или для одного моля
. (1.6)
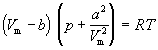
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.
Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов
Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление
(1.7)
(1.8)
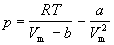
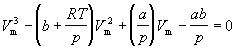
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.
На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы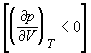 
. Состояния на участках 12 и 54, которые соответствуют переохлажденному пару и перегретой жидкости, соответственно, являются неустойчивыми (метастабильными) и могут быть лишь частично реализуемы в специальных условиях. Так, осторожно сжимая пар выше точки 1 (рис. 1.4), можно подняться по кривой 12. Для этого необходимо отсутствие в паре центров конденсации, и в первую очередь пыли. В этом случае пар оказывается в пересыщенном, т.е. переохлажденном состоянии. И наоборот, образованию капелек жидкости в таком паре способствуют, например, попадающие в него ионы. Это свойство пересыщенного пара используется в известной камере Вильсона (1912), применяемой для регистрации заряженных частиц. Движущаяся заряженная частица, попадая в камеру, содержащую пересыщенный пар, и соударяясь с молекулами, образует на своем пути ионы, создающие туманный след – трек, который фиксируется фотографически.
Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.
По мере повышения температуры все три корня сближаются, и при критической температуре Tc все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [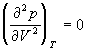
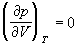
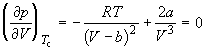
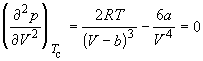
] с горизонтальной касательной [
], то есть
, (1.9)
. (1.10)
Совместное решение этих уравнений дает:
, (1.11)
, (1.12)
, (1.13)
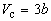
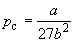
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Zc для всех газов должен быть равен
(1.14)
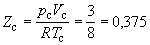
Из таблицы 1.2 видно, что хотя значение Zc для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;
2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);
3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).
Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).
Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору