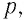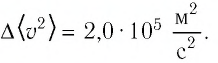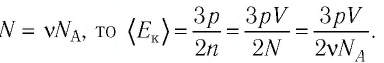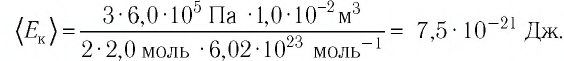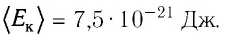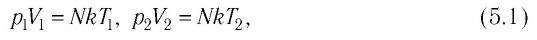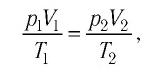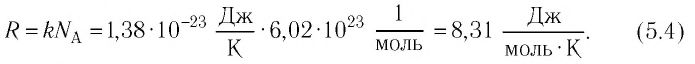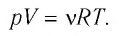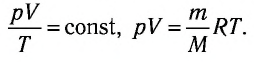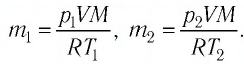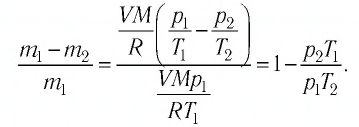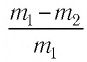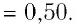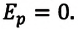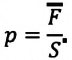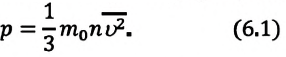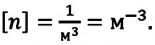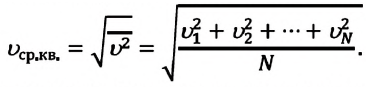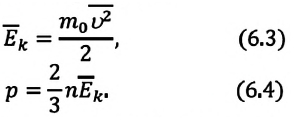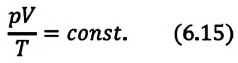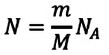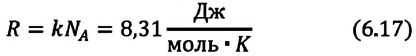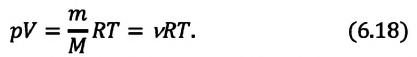Микроскопические параметры идеального газа

Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т.е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия.

где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (ºС).

Средние скорости молекул газов

Движение молекул газа подчиняется законам статистической физики. В каждый момент времени скорости отдельных молекул могут значительно отличаться друг от друга, но их средние значения одинаковы и при расчетах используются не мгновенные скорости отдельных молекул, а не которые средние значения. Различают среднюю арифметическую \(

\left\langle \upsilon \right\rangle\) и среднюю квадратичную \(

\left\langle \upsilon_ \right\rangle\) скорости хаотического движения молекул.

Средняя квадратичная скорость хаотического движения молекул

\left\langle \upsilon^2 \right\rangle\) — средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости\[

\left\langle \upsilon^2 \right\rangle \ne \left\langle \upsilon \right\rangle^2\].

См. также

Идеальный газ

Рассмотрим свойства газов на основе МКТ. Для этого введем физическую модель идеального газа, в которой приняты следующие допущения:

1) размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принимать за материальные точки;

2) силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;

3) молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами механики.

Таким образом, идеальным называется газ, в котором можно пренебречь собственным объемом молекул и межмолекулярным взаимодействием (кроме столкновений).

При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. Например, водород, кислород при нормальных условиях в атмосфере можно рассматривать как идеальные газы.

При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.

Основное уравнение МКТ идеального газа — это уравнение, связывающее микро- и макропараметры идеального газа. Одно из этих уравнений имеет вид:

где p — давление газа (Па); n — концентрация молекул (м –3 ); m₀ — масса одной молекулы газа (кг); 〈v 2 〉 — среднее значение квадрата скорости молекул (м/с 2 ). Это уравнение называют еще уравнением Клаузиуса.

Давление можно выразить через среднюю кинетическую энергию молекул\[

\left\langle E_k \right\rangle = \dfrac<2>,\] где 〈E_k 〉 – средняя кинетическая энергия одной молекулы газа (Дж). Подставляя 〈E_k 〉 в уравнение Клаузиуса, получаем

p = \dfrac 23 n \cdot \left\langle E_k \right\rangle. \quad (2)\)

Вывод основного уравнения

Температура – мера средней кинетической энергии молекул

Можно провести следующий эксперимент. Взять сосуды с разными газами. Определить предварительно их объемы, массы и рассчитать число молекул (по формуле \(

N = \dfrac mM \cdot N_A\)), затем поместить сосуды в тающий лед. После наступления теплового равновесия определить давление p и рассчитать отношение \(

\dfrac

\). Опыт показывает, что оно одинаково для всех газов. Затем эти сосуды помещают в кипящую воду. Опять это отношение для всех газов одинаковое, но большее первого значения. Проделав опыт несколько раз при разных температурах, можно заметить, что отношение \(

\dfrac

\sim T\). Обозначим коэффициент пропорциональности k, тогда:

\dfrac

= k \cdot T \) или \(

p = \dfrac \cdot k \cdot T = n \cdot k \cdot T, \quad (3)\)

где p — давление газа (Па); n — концентрация молекул (м –3 ); T — температура газа (К); k — постоянная Больцмана, равная 1,38·10 –23 Дж/К.

Сравнивая выражения (3) и (2), получаем

\( \dfrac 23 n \cdot \left\langle E_k \right\rangle = n \cdot k \cdot T, \) или \(

\left\langle E_k \right\rangle = \dfrac 32 k \cdot T. \)

Данная формула верна для расчёта средней энергии поступательного движения молекулы или для расчёта средней кинетической энергии одноатомной молекулы. Если учитывать, наряду с поступательным движением и вращение молекулы, то средняя кинетическая энергии молекулы с жесткой связью (без колебании атомов в молекуле) будет равна

\left\langle E_k \right\rangle = \dfrac i2 k \cdot T, \)

где i — степень свободы. Для одноатомного газа (например, инертные газы) i = 3, для двухатомного — i =5.

Температура – это величина, характеризующая среднюю кинетическую энергию поступательного движения молекул идеального газа:

Эта формула позволяет установить физический смысл абсолютной температуры Т. Этот макроскопический параметр характеризует среднее значение кинетической энергии хаотического теплового движения одной молекулы в состоянии термодинамического равновесия. Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом.

Так как абсолютная температура не может равняться нулю, то и средняя энергия теплового движения молекул то же не может равняться нулю, т.е. молекулы находятся в постоянном движении.

Источник

Содержание:

Идеальный газ:

Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).

Макро- и микропараметры:

При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление

Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.

Идеальный газ

Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.

Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.

Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.

Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.

Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле

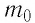
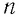
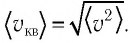
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу молекулы, концентрацию молекул и среднюю квадратичную скорость их теплового движения, определяемую по формуле Формула (3.1) связывает между собой макро- и микроскопические параметры системы «идеальный газ».

Зависимость давления газа от среднего значения квадрата скорости 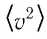теплового движения его молекул обусловлена тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками.

Обозначим через 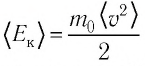среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет вид:

Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.

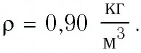
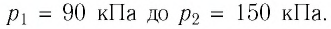
Баллон электрической лампы наполнен газом, плотность которого После включения лампы давление газа в ней увеличилось от Определите, на сколько при этом увеличился средний квадрат скорости теплового движения молекул газа.

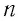
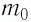
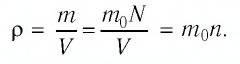
Решение. Покажем, что между плотностью р газа и концентрацией его частиц существует связь. Плотность вещества газа равна отношению массы к предоставленному ему объёму. Поскольку произведение массы одной молекулы и числа N молекул равно массе вещества, то:

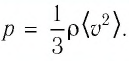
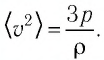
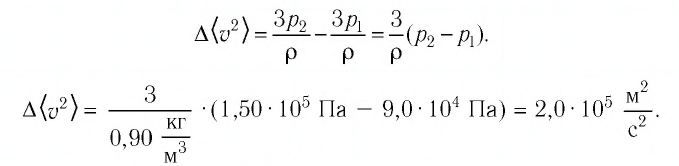
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: Следовательно, средний квадрат скорости теплового движения молекул газа Определим изменение среднего квадрата скорости теплового движения молекул газа после включения лампы:

Ответ:

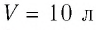
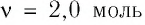
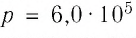
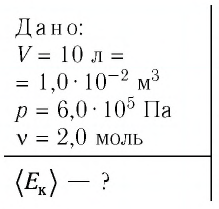
В сосуде вместимостью находится одноатомный газ, количество вещества которого и давление Па. Определите среднюю кинетическую энергию теплового движения атомов этого газа.

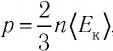
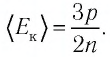
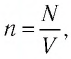
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде , следует, что Так как концентрация атомов а число атомов газа

Ответ:

Уравнение состояния идеального газа

Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.

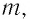
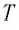
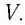
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса температура и объём Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.

Если при переходе идеального газа из одного состояния в другое число его т

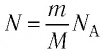
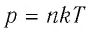
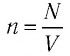
молекул остается постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений и следует:

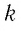
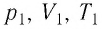
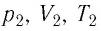
где — постоянная Больцмана; — параметры начального состояния газа, а — конечного. Из соотношений (5.1) следует, что

При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.

Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.

Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.

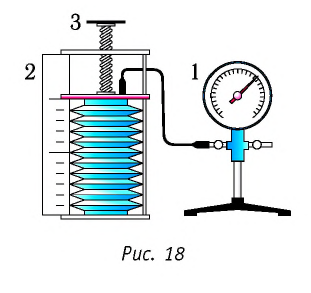
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

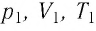
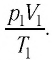
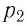
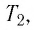
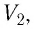
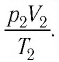
Измерив параметры газа в начальном состоянии, вычисляют отношение Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа и температуру а также рассчитав предоставленный ему объём вычисляют отношение Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.

Уравнение состояния (5.2) можно применять для газов при следующих условиях:

Поскольку число частиц 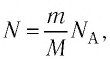то из уравнения (5.1) следует:

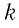
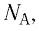
Величину, равную произведению постоянной Больцмана и постоянной Авогадро назвали универсальной газовой постоянной R:

С учётом выражения (5.4) уравнение (5.3) примет вид:

Поскольку количество вещества 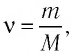то формулу (5.5) можно записать в виде:

Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.

Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.

Давление смеси газов

В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.

Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.

Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.

Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.

Смесь идеальных газов принимают за идеальный газ.

Из истории физики:

Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.

При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):

Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.

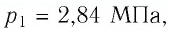
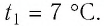
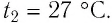
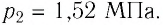
Баллон с газом, давление которого находился в неотапливаемом помещении, где температура воздуха После того как некоторое количество газа было израсходовано, баллон внесли в помещение, где температура воздуха Определите, какая часть газа была израсходована, если после длительного пребывания баллона в отапливаемом помещении давление газа в нём стало

Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:

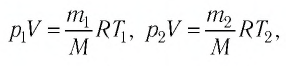
откуда

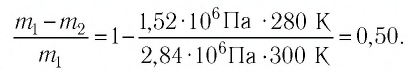
Ответ:

Основное уравнение молекулярно-кинетической теории идеального газа

В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.

Идеальный газ:

Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.

Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;

Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.

Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.

Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.

Основное уравнение молекулярно-кинетической теории идеального газа:

Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:

В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.

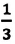
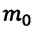
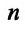
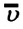
Где — количественный коэффициент, характеризующий трехмерность пространства и выражающий равноправность всех трех направлений в хаотическом движении молекул, — масса одной молекулы, — концентрация молекул, — средняя квадратичная скорость молекул.

Концентрация молекул — это число молекул в единице объема:

Единица концентрации в СИ:

Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:

Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:

Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.

Если принять во внимание, что плотность газа 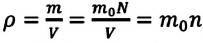в (6.1), то получится формула зависимости давления идеального газа от ее плотности:

Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.

Уравнение Клапейрона

Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.

Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:

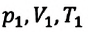
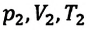
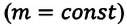
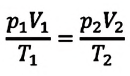
Где — параметры идеального газа в начальном состоянии, — параметры идеального газа в конечном состоянии. При помощи простых математических преобразований выражений (6.14) для идеального газа данной массы получим:

или

Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.

Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.

Уравнение Менделеева-Клапейрона:

Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,

в формуле (6.14), получим:

Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 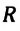и имеет числовое значение:

Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.

Физический смысл универсальной газовой постоянной определяется из последнего выражения.

Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.

Уравнение Менделеева-Клапейрона можно записать и в таком виде:

Где 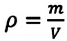— плотность газа.

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник